Remember the past: a comparison of time-adaptive training schemes for non-homogeneous regression

Non-homogeneous regression is a frequently used post-processing method for increasing the predictive skill of probabilistic ensemble weather forecasts. To adjust for seasonally varying error characteristics between ensemble forecasts and corresponding observations, different time-adaptive training schemes, including the classical sliding training window, have been developed for non-homogeneous regression. This study compares three such training approaches with the sliding-window approach for the application of post-processing near-surface air temperature forecasts across central Europe. The predictive performance is evaluated conditional on three different groups of stations located in plains, in mountain foreland, and within mountainous terrain, as well as on a specific change in the ensemble forecast system of the European Centre for Medium-Range Weather Forecasts (ECMWF) used as input for the post-processing.

The results show that time-adaptive training schemes using data over multiple years stabilize the temporal evolution of the coefficient estimates, yielding an increased predictive performance for all station types tested compared to the classical sliding-window approach based on the most recent days only. While this may not be surprising under fully stable model conditions, it is shown that “remembering the past” from multiple years of training data is typically also superior to the classical sliding-window approach when the ensemble prediction system is affected by certain model changes. Thus, reducing the variance of the non-homogeneous regression estimates due to increased training data appears to be more important than reducing its bias by adapting rapidly to the most current training data only.

1 Introduction

The need for accurate probabilistic weather forecasts is steadily increasing, because reliable information about the expected uncertainty is crucial for optimal risk assessment in agriculture and industry or for personal planning of outdoor activities. Therefore, most forecast centers nowadays issue probabilistic forecasts based on ensemble prediction systems (EPSs). To quantify the uncertainty of a specific forecast, an EPS provides a set of numerical weather predictions using slightly perturbed initial conditions and different model parameterizations (Palmer, 2002). However, due to various constraints and required simplifications in the EPS, these forecasts often show systematic biases and capture only parts of the expected uncertainty, especially when EPS forecasts are directly compared to point measurements (Gneiting and Katzfuss, 2014). In order to increase the predictive skill of the forecasts for specific locations, statistical post-processing is often applied to correct for these systematic errors in the forecasts' expectation and uncertainty.

One of the most frequently used parametric post-processing methods is “ensemble model output statistics” (EMOS) introduced by Gneiting et al. (2005). To emphasize that not only the errors in the mean but also the errors in the uncertainty are corrected, the method is often referred to as “non-homogeneous regression” (NR). In the statistical literature, this type of model is also known as distributional regression (Klein et al., 2014) since all parameters of a specific response distribution are optimized simultaneously conditional on respective sets of covariates.

As the error characteristics between the covariates, typically provided by the EPS, and the observations often show seasonal dependencies and might change inter-annually over time, different time-adaptive training schemes have been developed for NR models. Gneiting et al. (2005) proposed the so-called “sliding training window” approach where the training data set consists of EPS forecasts and observations of the most recent 30–60 d only. As soon as new data become available, the training data set and the statistical model are updated so that the estimated coefficients automatically evolve over time and adjust to changing error characteristics. This makes it very handy for operational use; however, little training data can sometimes yield unrealistic jumps in the estimated coefficients over time, especially if events which show a significantly different error characteristic enter the training data set. Therefore, to stabilize the temporal variability of the coefficient estimates, several approaches have been proposed in the literature. Scheuerer (2014) regularizes the estimation by only allowing the optimizer to slightly adjust the coefficient from day to day. In an alternative approach, Möller et al. (2018) extend the training data by using not only the days prior to estimation, but also the days centered around the same calendar day over all previous years available. This idea of using a rolling centered training data set over multiple years is similar to the concept of using annual cyclic smooth functions to capture seasonality as employed by Lang et al. (2019). These smooth functions are also known as regression splines (Wood, 2017), where the estimate of each point in the function only depends on data in its closer neighborhood; this allows for a smooth and stable evolution of the coefficients over the year.

Alternative time-adaptive models are based on historical analogs or non-parametric approaches. For approaches employing analogs (Junk et al., 2015; Barnes et al., 2019), training sets are selected to consist of past forecast cases with atmospheric conditions similar to those on the day of interest. Such methods may lead to models that are able to account for the flow dependency of EPS errors (Pantillon et al., 2018; Rodwell et al., 2018). However, the definition and computation of similarity measures are far from straightforward, and substantial methodological developments may be required to obtain suitably extensive training data sets for stable model estimation (Hamill et al., 2008; Lerch and Baran, 2017). For non-parametric approaches (Taillardat et al., 2016; Henzi et al., 2019) or semi-parametric approaches (Rasp and Lerch, 2018; Schlosser et al., 2019), time-adaptive choices of the training data are typically abandoned as well, as interactions between the day of the year and other covariates can capture the potential time adaptiveness. Therefore, analog-based and non-parametric approaches will not be pursued further in the context of this work.

In addition to the training scheme employed, an important data-specific aspect which has to be considered in post-processing is that the EPS may change over time (Hamill, 2018). This also motivates the recent study of Demaeyer and Vannitsem (2019), which introduces the promising concept of a post-processing method specifically dealing with model changes in a simplified physical setup. However, as stated by the authors, more research would be required to transfer their findings to real case scenarios. When using data of an operational EPS, changes in the underlying numerical model, e.g., an increased horizontal resolution, can typically lead to sudden transitions in the predictive performance of the EPS and hence affect the error characteristics of the data. If the training data set used to estimate the statistical post-processing model contains data of a previous EPS version which significantly differs from the current one, it can result in a loss of the predictive performance.

This paper presents a comparison of four widely used different time-adaptive training schemes proposed in the literature that employ alternative strategies to account for varying error characteristics in the data. To show a wide spectrum of possible approaches in a unified setup – rather than finding the universally best method – we consider typical basic applications of these training schemes and refrain from more elaborate tuning or combinations. A case study is shown for post-processed 2 m temperature forecasts for three different groups of stations across central Europe at the midlatitudes, namely, stations in the plain, in the foreland, and within mountainous terrain (Fig. 1). The study highlights the advantages and drawbacks of the different approaches in different topographical environments and investigates the impact of a change in the horizontal resolution of the EPS, which is expected to have a particularly pronounced effect on the predictive performance.

The structure of the paper is as follows: Sect. 2 explains the different methods and the comparison setup including the underlying data. In Sect. 3, the different time-adaptive training schemes are compared in terms of their coefficient paths and their predictive performance. Finally, a summary and conclusion are given in Sect. 4.

2 Methodology and comparison setup

The different training schemes for NR models proposed in the literature try to adapt to various kinds of error sources that can occur in post-processing, both in space and time. In order to provide a unifying view and to fix jargon, we first discuss these different error sources and then introduce the training schemes considered along with the comparison setup employed.

2.1 Sources of errors in post-processing

NR models aim to adjust for errors and biases in EPS forecasts but, of course, the NR models can be affected by errors and misspecifications themselves. Therefore, we try to carefully distinguish between the two different models involved with their associated errors, i.e., the numerical weather prediction model underlying the EPS vs. the statistical NR model employed for post-processing.

The skill of the EPS can be quantified in EPS forecast biases and variances, which (i) typically vary for different locations conditional on the surrounding terrain, (ii) often show cyclic seasonal patterns, and (iii) can experience non-seasonal temporal changes, e.g., due to changes in the EPS itself.

In addition to the error sources in the employed EPS, the performance of the statistical post-processing itself will typically also (iv) differ at different measurement sites, (v) strongly depend on the amount of training data used, and (vi) whether it is affected by effects that are not accounted for in the NR specification.

Clearly, larger training samples (v) will lead to more reliable predictions when the NR specification (vi) – in terms of response distribution, covariates and corresponding effects, link functions, estimation method, etc. – appropriately captures the error characteristics in the relationship between EPS forecasts and actual observations. However, when these error characteristics differ in space (i and iv) and/or in time (ii and iii), it is not obvious what the best strategy for training the NR is. Extending the training data (v) in space or time will reduce the variance of the NR estimation but might also introduce bias if the NR specification (vi) is not adapted. Thus, this is a classical bias-variance trade-off problem, and we investigate which strategies for dealing with this are most useful in a typical temperature forecasting situation.

To fix jargon, we employ the terms “model” and “bias” without further qualifiers when referring to the NR model in post-processing, whereas when referring to the numerical weather prediction model we employ “EPS model“ and “EPS bias”. Moreover, we refer to a statistical model whose estimates have small bias and variance as stable.

2.2 Non-homogeneous regression with time-adaptive training schemes

Non-homogeneous regression as originally introduced by Gneiting et al. (2005) is a special case of distributional regression, where a response variable y is assumed to follow a specific probability distribution 𝒟 with distribution parameters ${\mathit{\theta }}_k,k=\mathrm{1},\mathrm{\dots },K$:

$$\begin{array}{}\text{(1)}& y\sim \mathcal{D}({\mathit{\theta }}_{\mathrm{1}},\mathrm{\dots },{\mathit{\theta }}_K)=\mathcal{D}\left(h_{\mathrm{1}}\right({\mathit{\eta }}_{\mathrm{1}}),\mathrm{\dots },h_K({\mathit{\eta }}_K\left)\right),\end{array}$$

where each parameter of the distribution is linked to an additive predictor η_k via a link function h_k to ensure its appropriate co-domain. In the case of post-processing air temperatures, the normal distribution is typically employed (Gneiting and Katzfuss, 2014), and Eq. (1) can be rewritten as

$$\begin{array}{}\text{(2)}& y\sim \mathcal{N}(\mathit{\mu },\mathit{\sigma }).\end{array}$$

In the classical NR (Gneiting et al., 2005), the two distribution parameters location μ and scale σ are expressed by the ensemble mean m and ensemble variance or standard deviation s, respectively:

$$\begin{array}{}\text{(3)}& {\displaystyle }\mathit{\mu }={\mathit{\eta }}_{\mathit{\mu }}={\mathit{\beta }}_{\mathrm{0}}+{\mathit{\beta }}_{\mathrm{1}}\cdot m,\text{(4)}& {\displaystyle }\log \left(\mathit{\sigma }\right)={\mathit{\eta }}_{\mathit{\sigma }}={\mathit{\gamma }}_{\mathrm{0}}+{\mathit{\gamma }}_{\mathrm{1}}\cdot s,\end{array}$$

with β_• and γ_• being the corresponding intercept and slope coefficients. Here, we use the logarithm link to ensure positivity of the scale parameter σ; however, a quadratic link with additional parameter constraints for the coefficients as used by Gneiting et al. (2005) would also be feasible. In this study, we regard the statistical model specifications according to Eqs. (2)–(4), but all concepts of time-adaptive training schemes could easily be transferred to other response distributions 𝒟, to alternative link functions h(⋅), or to more complex additive predictors η with additional covariates.

The regression coefficients β_• and γ_• are estimated by minimizing a loss function over a training data set containing historical pairs of observations and EPS forecasts. In this study, we employ maximum likelihood estimation, which performs very similarly to minimizing the continuous ranked probability score (CRPS, Gneiting and Raftery, 2007) as used by Gneiting et al. (2005) when the response distribution is well specified (Gebetsberger et al., 2018). For a single observation y, the log-likelihood L of the normal distribution is given by

$$\begin{array}{}\text{(5)}& L(\mathit{\mu },\mathit{\sigma }|y)=\log \left\{{\displaystyle \frac{\mathrm{1}}{\mathit{\sigma }}}\mathit{\varphi }\left({\displaystyle \frac{y-\mathit{\mu }}{\mathit{\sigma }}}\right)\right\},\end{array}$$

where ϕ(⋅) is the probability density function of the normal distribution. The coefficients β_• and γ_•, specified in Eqs. (3) and (4), are derived by minimizing the sum of negative log-likelihood contributions L over the training data. The larger the training data, the more stable the estimation in case the statistical model is well specified; however, if the covariate's skill varies either seasonally or non-seasonally over time, this leads to the bias-variance trade-off between preferable large training data sets for stable estimation and the benefit of shorter training periods which allow one to adjust more rapidly to changes in the data or, to be precise, in the error characteristics of the data (see Sect. 2.1). In the following, four approaches are discussed on how to gain informative time-adaptive training data sets while ensuring a stable estimation.

2.2.1 Sliding-window

The sliding-window approach originally introduced by Gneiting et al. (2005) uses the most recent days prior to the day of interest as training data for estimation. For post-processing 2 m temperature forecasts, Gneiting et al. (2005) found the best predictive performance for training periods between 30 and 45 d with substantial gains in increasing the training period beyond 30 d and slow but steady performance losses for training lengths beyond 45 d. According to Gneiting et al. (2005), the latter is presumably a result of seasonally varying EPS forecast biases.

In this study, we use a period of 40 d for the sliding-window approach, which is a frequently used compromise (e.g., Baran and Möller, 2017; Gneiting et al., 2005; Wilson et al., 2007). However, as discussed in Gneiting et al. (2005), different training periods might perform better for distinct weather variables, locations, forecast steps, or model specifications. Common choices in the literature include training lengths between 15 and 100 d, for example, depending on whether the estimation of regression coefficients is performed station-specifically or jointly for multiple locations at once.

2.2.2 Regularized sliding-window

A regularized adaption of the classical sliding-window approach was introduced by Scheuerer (2014) in order to stabilize the estimation based on early stopping in statistical learning. The motivation is that gradient-based optimizers adjust the starting values by iteratively taking steps in the direction of the steepest descent of a distinct loss function until some convergence condition is fulfilled. These steps are largest in the first iteration and get smaller towards the optimum. Thus, the most important adjustments are made during the first steps, while further adjustments often improve the fit to unimportant or even random features in the data, which can lead to wiggly coefficient paths over time and ultimately to an overfitting (Scheuerer, 2014).

Therefore, Scheuerer (2014) proposes to use the coefficients of the previous day as starting values and to stop the optimizer after a single iteration to stabilize the evolution of the coefficient estimates. A drawback of his approach is that it implies that the estimation never converges and, in the case of poor starting values or strong truly observed temporal changes in the data, the obtained coefficients might be incorrect (Scheuerer, 2014). For post-processing precipitation amounts employing a left-censored generalized extreme value distribution, Scheuerer (2014) obtained better results with regularized coefficients than without regularization.

For the regularized sliding-window approach used in this study, we employ the quasi-Newton Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm as in Scheuerer (2014) and stop the optimizer after one single iteration. For the first time, we let the BFGS algorithm perform 10 iterations and use $({\mathit{\beta }}_{\mathrm{0}},{\mathit{\beta }}_{\mathrm{1}}{)}^{\top }=(\mathrm{0},\mathrm{1}{)}^{\top }$ as starting values in the location parameter μ and $({\mathit{\gamma }}_{\mathrm{0}},{\mathit{\gamma }}_{\mathrm{1}}{)}^{\top }=(\mathrm{0.1},\mathrm{1}{)}^{\top }$ as starting values in the scale parameter σ. According to Scheuerer (2014) a single iteration might not always provide the optimum degree of regularization; however, for the presented comparison study a single iteration yields a regularized setup which is on the opposite side of the possible model spectrum compared to the classical sliding-window approach which runs until convergence. In comparison to Scheuerer (2014), we perform maximum likelihood estimation instead of CRPS minimization.

2.2.3 Sliding-window plus

As already pointed out by Gneiting et al. (2005), training data from previous years could additionally be included in the sliding-window approach to address seasonal effects. This should reduce the variance in the estimation of the regression coefficients, which stabilizes the evolution of the coefficients similarly to the regularized sliding-window approach.

This idea has recently been pursued by Vogel et al. (2018) for the construction of climatological reference forecasts and by Möller et al. (2018) for a post-processing approach based on D-vine copulas in which many more coefficients than in classical NR need to be estimated, making a more extensive training data set necessary. Their so-called “refined training data set” consists of the most 45 recent days prior to the day of interest plus 91 d centered around the same calendar day over all previous years available. Including multiple years yields more stable estimates, while, on the other hand, there is the trade-off of losing the ability to quickly adjust to non-seasonal temporal changes in the EPS forecast biases. The approach of Möller et al. (2018) can be seen as time-adaptive version of the seasonal training proposed by Hemri et al. (2016), who consider training data sets comprised of days from all previous years within the same season (winter/summer).

In this study, to be comparable to the sliding-window approach, we use the most recent 40 d prior to estimation and a respective 81 d interval centered around the day of interest over the previous years available in the training data.

2.2.4  Smooth model

If we reformulate the sliding-window plus approach, it is very similar to fitting an annual cyclic smooth function where the points of the function only depend on data points in the closer neighborhood, specified by the sliding-window length.

Cyclic smooth functions belong to the broader model class of generalized additive models (GAMs, Hastie and Tibshirani, 1986), which allow one to include potentially nonlinear effects in the linear predictors η. Smooth functions are also referred to as regression splines and are directly linked to the model parameters as additive terms in η. Introductory material for cyclic smooth functions conditional on the day of the year can be found in Lang et al. (2019), and a comprehensive summary of GAMs is given in Wood (2017).

To account for seasonal variations we only need to fit one single model, here called the smooth model, over a training data set with several years of data. The effects included allow the coefficients to smoothly evolve over the year, which leads to the following adaptations in Eq. (3) and (4) for the location μ and scale σ, respectively:

$$\begin{array}{}\text{(6)}& {\displaystyle }\mathit{\mu }={\mathit{\eta }}_{\mathit{\mu }}={\mathit{\beta }}_{\mathrm{0}}+f_{\mathrm{0}}\left(\text{doy}\right)+({\mathit{\beta }}_{\mathrm{1}}+f_{\mathrm{1}}(\text{doy}\left)\right)\cdot m,\text{(7)}& {\displaystyle }\log \left(\mathit{\sigma }\right)={\mathit{\eta }}_{\mathit{\sigma }}=\underset{\begin{array}{c}\text{seasonally varying}\\ \text{intercept}\end{array}}{\underbrace{{\mathit{\gamma }}_{\mathrm{0}}+g_{\mathrm{0}}\left(\text{doy}\right)}}+\underset{\begin{array}{c}\text{seasonally varying}\\ \text{slope}\end{array}}{\underbrace{({\mathit{\gamma }}_{\mathrm{1}}+g_{\mathrm{1}}(\text{doy}\left)\right)}}\cdot s,\end{array}$$

with m and s being the ensemble mean and ensemble standard deviation, respectively; β_• and γ_• are regression coefficients, and f_•(doy) and g_•(doy) employ cyclic regression splines conditional on the day of the year (Wood, 2017). The regression coefficients β₀ and γ₀, as well as β₁ and γ₁, are unconditional on the day of the year and can be interpreted as global intercept or slope coefficients, respectively.

Table 1 Overview of time-adaptive training schemes, distinguished by model specification/estimation and training data selection corresponding to errors sources (vi) and (v), respectively. The basic model specification refers to Eqs. (3)–(4), in contrast to the extended Eqs. (6)–(7).

2.3 Comparison setup

2.3.1 NR training schemes

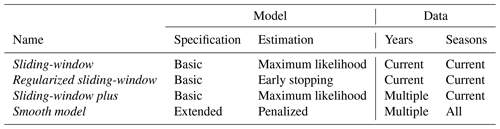
The NR training schemes presented in Sect. 2.2 deal with the potential temporal error sources from Sect. 2.1 in different ways (see Table 1 for an overview). The classic sliding-window employs the basic NR model equations from Eqs. (3) to (4) and avoids potential biases in the NR model estimation by using only very recent data from the same year and season. Compared to this, the regularized sliding-window and sliding-window plus approaches both try to stabilize the coefficient estimates by reducing the variance – either through regularized estimation (vi) or by considering multiple years (v). The smooth model differs from all of these by modifying both the model (vi) and data (v) specification, using the extended model specification from Eqs. (6) to (7) fitted by penalized estimation to a large data set comprising several years and all seasons.

Potential spatial differences (i) and (iv) are handled for all training schemes in the same way: the NR models are estimated separately for each station and subsequently evaluated in groups of terrain types (plain, foreland, alpine). The underlying EPS data – described subsequently – are the same for all NR training schemes and are thus affected by the same seasonal (ii) and non-seasonal changes (iii).

2.3.2 Data sets

For validation of the training schemes, we consider 2 m temperature ensemble forecasts and corresponding observations at 15 measurement sites located across Austria, Germany, and Switzerland. The sites are chosen to investigate the impact of potential error sources in space (i) and (iv), e.g., through varying discrepancies between the real and EPS topography. The data comprises three groups of five stations located either in plains, in mountain foreland, or within mountainous terrain (see Fig. 1). The estimated statistical models for stations Hamburg and Innsbruck, highlighted by symbols with white borders, are discussed in more detail in Sect. 3.1.

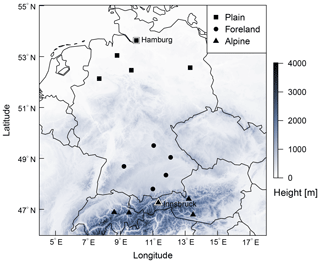
Figure 1 Overview of the study area with selected stations classified as plain, foreland, and alpine station sites. The two highlighted and labeled stations, Hamburg and Innsbruck, are discussed in detail in Sect. 3.1. Elevation data are obtained from the SRTM-30 m digital elevation model (NASA JPL, 2013).

As covariates for Eqs. (3)–(7), we employ the ensemble mean m and the ensemble standard deviation s of bilinearly interpolated 2 m temperature forecasts issued by the global 50-member EPS of the European Centre for Medium-Range Weather Forecasts (ECMWF). We assess forecast steps from +12 to +72 h ahead at a 12-hourly temporal resolution for the EPS run initialized at 00:00 UTC and use data from 8 March 2010 to 7 March 2019.

This period has been selected in order to investigate the impact of non-seasonal long-term changes in the EPS model (iii) that is not reflected in the NR model specifications; i.e., the horizontal resolution of the ECMWF EPS changed from the previous version (cycle 36r1; 26 January 2010) to the new version on 8 March 2016 (cycle 41r2). This specific model change was chosen among various others as it modifies the height of the terrain and, thus, likely introduces an EPS bias for temperature forecasts directly affecting the coefficient estimates; other changes such as modified model parameterizations or improvements in the analysis scheme are expected to have a minor impact on the post-processing of 2 m temperatures. It is of specific interest how the sliding-window plus and the smooth model are affected if the training period comprises data from both the “old EPS version” before the change in the horizontal resolution as well as the “new EPS version”. Thus, we construct three data sets with different validation periods that are either (a) not affected by this EPS model change at all, (b) start immediately after the model change, or (c) have some time lag after change.

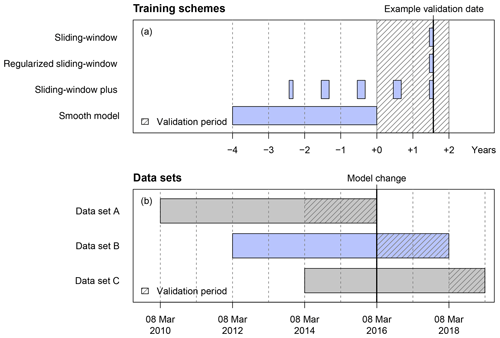
Figure 2 (a) Illustrative example of how the training data sets are composed for the four different time-adaptive training schemes. (b) Schematic overview of the training and validation data sets employed in this study with regard to the change in the horizontal resolution of the ECMWF EPS on 8 March 2016 (cycle 41r2). For training, up to 4 years of data are used in all data sets; for validation, 2 years of data are used for data sets A and B, and 1 year for data set C.

To understand how this affects the different training schemes, we first illustrate in Fig. 2a how training and validation periods are selected for each scheme. For the three sliding-window approaches, the NR models are re-estimated every day as the validation date rolls through the validation period (hatched area). In contrast, the smooth model is estimated only once for the entire validation period based on a fixed training data period of 4 years prior to the validation period. For a fair comparison, the training data for the sliding-window plus model are also restricted to 4 years prior to each validation date.

Now Fig. 2b illustrates how the three data sets A, B, and C are selected in relation to the EPS change on 8 March 2016.

• Data set A. All models are trained and evaluated without being affected by the EPS change.

• Data set B. All models start with a training period entirely before the EPS change but a validation period entirely after the change. However, for the sliding-window and regularized sliding-window approaches, the training period quickly rolls across the change point, and after 40 d they are not affected by it anymore. For sliding-window plus the training data also roll into the new EPS version but still partially use data from the old EPS version. Finally, as the smooth model is only estimated once, it cannot adapt at all to the new EPS version.

• Data set C. Effects from A and B are mixed so that the smooth model and the sliding-window plus model use data from both the old and new EPS versions, while the classical sliding-window and regularized sliding-window models already use only data from the new EPS version.

The validation period is 2 years for A and B and 1 year for C. A total number of 731/730/365 NR models has to be estimated for the three sliding-window approaches, while only 1/1/1 smooth model is required for data sets A/B/C per station and forecast step. The computation time for the various sliding-window approaches is in the order of seconds, whereas the estimation of the smooth model, including full Markov chain Monte Carlo (MCMC) sampling, is in the order of minutes on a standard computer.

3 Results

This section assesses the performance of the different time-adaptive training schemes. First, the temporal evolutions of the estimated coefficients are shown for two stations representative of one measurement site in the plains and one in mountainous terrain. Afterwards, the predictive performance of the training schemes is evaluated in terms of the CRPS conditional on the three data sets with and without the change in the horizontal resolution of the EPS (Fig. 2) and grouped for stations classified as topographically plain, mountain foreland, and alpine sites (Fig. 1).

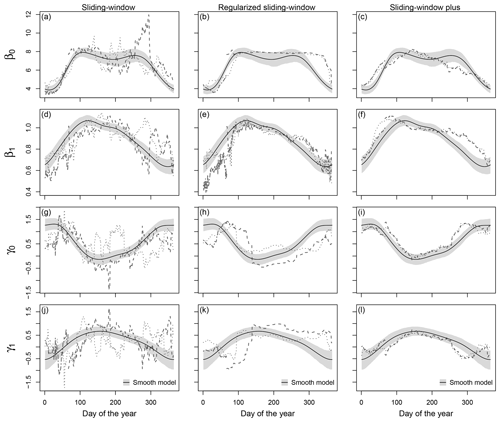
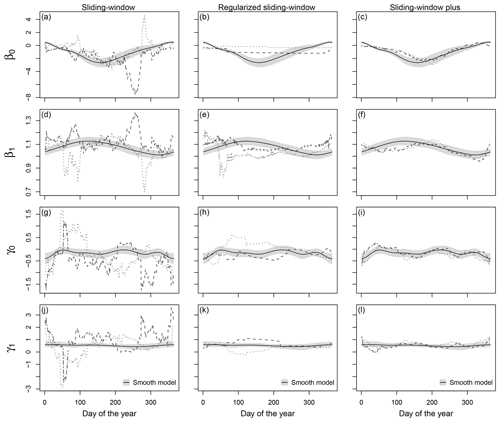
Figure 3 Temporal evolution of regression coefficients for the validation period in data set A for Innsbruck at forecast step +36 h (valid at 12:00 UTC). The coefficient paths are shown for the coefficients β₀ (a–c) and β₁ (d–f) in the location parameter μ and for the coefficients γ₀ (g–i) and γ₁ (j–l) in the scale parameter σ based on the sliding-window, regularized sliding-window, and sliding-window plus approaches (dashed, from left to right) compared to the smooth model approach (solid line). The coefficient paths are plotted for the consecutive calendar years 2014, 2015, and 2016 as dashed, dotted, and two-dashed lines, respectively. The grey shading represents the 95 % credible intervals of the coefficients in the smooth model based on MCMC sampling.

Figure 4 As Fig. 3 but for Hamburg at forecast step +36 h (valid at 12:00 UTC).

3.1 Coefficient paths

Figure 3 shows the estimated coefficients for Innsbruck at forecast step +36 h conditional on the day of the year. The coefficient paths are plotted for the different time-adaptive training schemes for 2 years included in the validation period of data set A. The pronounced seasonal evolution of the coefficients for all training schemes shows that the EPS' forecast bias and skill varies seasonally, which makes a time-adaptive training scheme mandatory to capture these characteristics in the post-processing. During summer, a slope coefficient β₁ close to 1 in the location parameter μ and a high slope coefficient γ₁ in the scale parameter σ indicate a better performance of the EPS compared to the cold season.

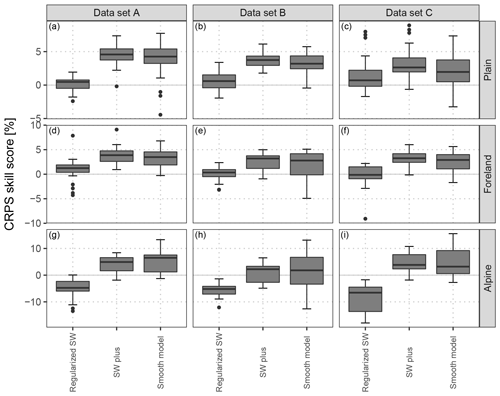
Figure 5 CRPS skill scores clustered into groups of stations located in the plain, in the mountain foreland near the Alps, and within mountainous terrain and for the out-of-sample validation periods according to the different data sets: data set A without the change in the horizontal resolution of the EPS, data set B with the EPS change in between the training and validation data sets, and data set C with the EPS change within training data (Fig. 2). Compared are the different time-adaptive training schemes specified in Sect. 2.2 with the classical sliding-window approach as a reference; note that “sliding-window” is abbreviated as SW in the figure. Each box-and-whisker contains aggregated skill scores over the forecast steps from +12 to +72 h at a 12-hourly temporal resolution and over five respective weather stations (Fig. 1). Skill scores are in percent and positive values indicate improvements over the reference.

In comparison to the other time-adaptive training schemes, the classical sliding-window approach (Fig. 3a, d, g, j) shows very strong outliers and an unstable temporal evolution for all coefficients with distinct differences during the 2 subsequent validation years; this is more pronounced for the scale parameter σ where the estimates seem to be more volatile than for the location parameter μ. All strategies extending the classical sliding-window approach smooth the temporal evolution of the coefficients to a certain extent while maintaining the overall seasonal cyclic pattern. For the regularized sliding-window approach (Fig. 3b, e, h, k), the stabilization strongly differs for the individual coefficients, and some of the estimated coefficients seem to need rather long to adapt during the transition periods; the latter could indicate that a single iteration step might not be sufficient in this study. The coefficient paths for the sliding-window plus approach (Fig. 3c, f, i, l) and for the smooth model (Fig. 3a–l; solid line) look very similar with minor distortions during the cold season. Due to the definition of the smooth model, its coefficient paths show the most stable evolution but with the lowest ability to react to abrupt changes in the error characteristics.

For Hamburg (Fig. 4) by contrast to Innsbruck, the information content of the mean EPS temperature forecast is quite high throughout the year. This yields a lower bias correction and an almost one-to-one mapping of the ensemble mean to the location parameter μ indicated by a coefficient β₁ close to 1. Despite the different post-processing characteristics, the temporal evolution of the coefficient paths is similar to the one for Innsbruck, which confirms our previous findings: for the extended sliding-window approaches the coefficients have indeed very little seasonal variability, while for the classical sliding-window approach the coefficients show unrealistically strong fluctuations over time without a clear seasonal pattern (Fig. 4a, d, g, j). As for Innsbruck, the regularized sliding-window approach has a rather unrealistic stepwise evolution for some coefficients (Fig. 4b, e, h, k). The coefficient paths for the sliding-window plus approach (Fig. 4c, f, i, l) and the smooth model (Fig. 4; solid line) look comparable. These results support the bias-variance trade-off where regularizing or smoothing stabilizes the coefficient paths while losing the ability to rapidly react to temporal changes in the data.

3.2 Predictive performance

After the illustrative evaluation of the coefficients' temporal evolution for the different time-adaptive training schemes, Fig. 5 shows aggregated CRPS skill scores for groups of five respective stations classified as topographically plain, mountain foreland, and alpine sites (Fig. 1) regarding data sets A, B, and C (Fig. 2). In all panels the regularized sliding-window approach, the sliding-window plus approach, and the smooth model are compared to the classical sliding-window approach as a reference.

• For data set A, the regularized sliding-window approach shows only little improvements for the plain and foreland and an overall performance loss for alpine stations. By contrast, the sliding-window plus and smooth model approaches show distinct improvements over the classical sliding-window approach, with the largest values for alpine sites.

• For data set B at stations in the plains and foreland, the mean predictive skill behaves similarly to data set A, except that the smooth model shows a slightly larger variance. For alpine stations, the regularized sliding-window approach performs slightly worse than in data set A, while the two approaches using training data over multiple years no longer outperform the reference.

• For data set C at stations in the plains and foreland, the predictive skill is again similar to data set A with slight performance losses. For alpine stations, the regularized sliding-window approach shows even less skill than in data set B, while the two other approaches again outperform the sliding-window approach and are on a similar level to that in data set A.

The validation of the different time-adaptive training schemes shows that the sliding-window plus approach and the smooth model perform overall similarly and are clearly superior for all station types compared to the classical sliding-window approach. However, the smooth model shows the highest variance in the predictive performance in the case of a change in the EPS, especially in mountainous terrain (data sets B and C); this is likely due to its reduced ability to adapt to temporal changes in the data. Furthermore, the validation shows that the regularized sliding-window approach seems to have difficulties in mountainous terrain and yields only minor improvements for plain and foreland sites.

4 Summary and conclusion

Non-homogeneous regression (NR) is a widely used method to statistically post-process ensemble weather forecasts. In its original version it was used for temperature forecasts employing a Gaussian response distribution, but over the last decade various statistical model extensions have been proposed for other quantities employing different response distributions or to enhance its predictive performance. When estimating NR models there is always a trade-off between large enough training data sets to get stable estimates and still allowing the statistical model to adjust to temporal changes in the statistical error characteristics of the data. Therefore, different training schemes with specific advantages and drawbacks have been developed as presented in this paper. To show a wide spectrum of possible approaches in a unified setup, we consider typical basic applications of the training schemes and refrain from more elaborate tuning or combinations.

The classical sliding-window approach has the advantage that no extensive training data set is required, which allows the statistical model to adjust itself rapidly to changing forecast biases, for example, in the case of changes in the EPS. On the other hand, statistical models trained on a small training data set have typically large variance in the estimation of the regression coefficients, which can yield unstable wiggly coefficient paths. Additional regularization allows one to stabilize the evolution of the regression coefficients without losing the simplicity of the classical sliding-window approach. However, inappropriate settings of the optimizer, e.g., unrealistic starting values or insufficient update steps, can quickly lead to incorrect coefficients. The alternative sliding-window plus strategy foregoes regularization but stabilizes the coefficients by using an extended training data set which includes data from the same season over several years. Compared to the classical approach the method requires historical data and partially loses its ability to rapidly adjust to changes in the error characteristics. The last approach presented in this paper can be seen as a generalization of the sliding-window plus approach. Rather than using a training data set centered around the date of interest, the smooth model makes use of all historical data in combination with cyclic regression splines, which allows the coefficients to smoothly evolve over the year.

The differences between the methods presented can be seen in the coefficient paths shown in Figs. 3 and 4. The coefficients of the classical sliding-window approach show strong fluctuations and pronounced peaks throughout the year. Regularization allows one to stabilize the evolution; however, strong step-wise changes in the coefficient paths still occur. The two methods using data from multiple years perform comparably similarly and show stable coefficient paths over the year. Figure 5 confirms that more stable estimates have a positive impact on the predictive performance. The sliding-window plus approach and the smooth model show an overall improvement of about 3 %–5 % (in median) over the classical sliding-window approach, while the regularized sliding-window only partially outperforms the sliding-window training scheme. Even in the case of the model change chosen to demonstrate the effect of non-seasonal long-term changes on the coefficient estimates, the training schemes using multiple years of data are still superior to the ones using the most recent days only, even if they technically allow adjustment to the EPS change more rapidly.

To conclude, all four training schemes shown in this paper have their advantages in particular applications. If only short periods of training data are available (<1 year), the classical sliding-window approach may already provide sufficiently good estimates. However, as soon as one has access to longer historical data sets, the approaches using data from multiple years become superior due to a more stable coefficient evolution over time, which yields an overall improved performance. This even holds in the case of the EPS change considered in this study, but may be different for other changes or EPSs. While the sliding-window plus approach is a natural extension of the classical sliding-window approach and, therefore, can be estimated by the same software, the smooth model approach can be seen as a generalization, and only a single model has to be estimated for all seasons using all available data. The smooth model yields, by definition, the smoothest and most stable coefficient paths but with the lowest ability to adjust itself to a new error characteristic.