Dynamically optimal models of atmospheric motion

A derivation of discrete dynamical equations for the dry atmosphere in the absence of dissipative processes based on the least action (i.e. Hamilton's) principle is presented. This approach can be considered the finite-element method applied to the calculation and minimization of the action. The algorithm possesses the following characteristic features:

1. For a given set of grid points and a given forward operator (i.e. the mode of interpolation), through the minimization of action, the algorithm ensures maximal closeness (in a broad sense) of the evolution of the discrete system to the motion of the continuous atmosphere (a dynamically optimal algorithm).

2. The grid points can be irregularly spaced, allowing for variable spatial resolution.

3. The spatial resolution can be adjusted locally while executing calculations.

4. By using a set of tetrahedra as finite elements the algorithm ensures a better representation of the topography (piecewise linear rather than staircase).

The algorithm automatically calculates the evolution of passive tracers by following the trajectories of the fluid particles, which ensures that all tracer properties required a priori are satisfied. For testing purposes, the algorithm is realized in 2D, and a numerical example representing a convection event is presented.

1 Introduction

The models simulating atmospheric dynamics are often built by replacing spatial and temporal derivatives in the continuous equations of motion (like conservation of momentum or mass) by corresponding finite-difference approximations. In finite-volume versions, the discrete approximations of spatial derivatives are also used for calculation of fluxes. There are numerous ways to proceed based on experience accumulated amongst different disciplines. The approaches that start from the continuous equations of motion and are pursued along these lines essentially ignore, however, the fact that the governing equations representing atmospheric dynamics themselves follow from the least action, or Hamilton's, principle (Eckart, 1960; Salmon, 1983) (LAP for brevity), and it is reasonable to take advantage of this fact. LAP states that the action, which is a time integral of the difference between the total kinetic and potential energy (i.e. the Lagrangian) of the system, is minimal for the actual evolution of a mechanical system. Application of LAP leads to the Euler–Lagrange equations of motion, which include the second-order derivatives of the state variables in time. By using the Liouville transformation, these equations can be cast into the Hamiltonian equations, which, being resolved with respect to the first-order time derivatives, are thus better amenable to both analytical and numerical solutions (Salmon, 1988).

To build a computer model of atmospheric motion, one has to pass from a continuous to a discrete system. There are at least two ways to achieve this within the Lagrangian/Hamiltonian approach. The first one is to replace a continuous Hamiltonian or Lagrangian by a discrete analogue (Salmon, 1983). If the Hamiltonian equations are formulated in non-canonical coordinates (e.g. Rolstone and Bruce, 1995), one also has to approximate the Poisson bracket (Eldred et al., 2019; Salmon, 2004). By maintaining corresponding symmetries, one also tries to ensure that the conservation laws of the original equations are inherited by the discretized ones as well (Salmon, 2004). An important advantage of the Hamiltonian and Lagrangian descriptions is that different approximations (like quasi-hydrostatic) can be done within this approach by modifying the corresponding Hamiltonian or Lagrangian (Shutts, 1989; Salmon and Smith, 1994; Rolstone and Bruce, 1995).

The second way is after selection of a discrete set of parameters (i.e. the finite number of degrees of freedom) to approximate an action of the continuous atmosphere. To do this, one has also to choose an observation (or forward) operator, i.e. a mode of interpolation allowing the state of the atmosphere to be unambiguously calculated at any spatial point based on the set of discrete parameters. Using this operator, one calculates approximately the action density of the continuous atmosphere in terms of the discrete parameters; integrates it over the space; and, by minimizing the result, obtains ordinary differential equations (ODEs) governing their evolution. Such an approach seems to be more consistent than approximating a Hamiltonian or Lagrangian. From this standpoint replacement of the continuous Hamiltonian/Lagrangian by a discrete analogue can be considered to be a piecewise-constant spatial approximation of the corresponding density. One can, however, use more accurate approximations; in this work, in particular, a piecewise-linear approximation is applied instead. In this case, the fields of atmospheric variables become piecewise continuous. One can refer to such atmospheric models as “dynamically optimal”, since for a given set of discrete parameters and a given mode of interpolation, the governing ODEs follow unambiguously, ensuring minimal action and thus the best approximation (from the standpoint of action minimization) of the dynamics of a continuous atmosphere. Such an approach is essentially a combination of the finite-element method and LAP.

The approach based on approximation of continuous action was considered recently in Gawlik and Gay-Balmaz (2021). In this work, however, an action of the compressible atmosphere was calculated in non-canonical coordinates, which leads to a minimization of action under certain constraints on variations. This interesting technique differs significantly from the approach pursued in this paper where the action is calculated in the canonical coordinates and there are no restrictions on the coordinates/momenta variations.

We are considering in this work the approximation of the action in a spatial domain by assuming only continuous dependence on time. However, one can discretize the calculation of action, not only in the spatial domain but in the time domain as well. Corresponding discrete time-evolution schemes are called variational integrators (Mardsen and West, 2001; Lew et al., 2003). Such an approach allows us to also use different time steps in different areas (asynchronous variational integrators), an option which should be of interest to the development of dynamical cores for weather and climate prediction models.

2 The action for a continuous atmosphere

This section describes mostly standard transformations (see, for example, Eckart,1960; Salmon,1988; Shutts,1989; Salmon and Smith, 1994) that precede the transition from continuous to discrete forms for the governing equations. Here, we will consider the case of a dry, rotating atmosphere, which is a base of a dynamical core. We begin with the following Eulerian equations that represent the adiabatic motion of dry air in the absence of losses:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& {\partial }_t\mathit{v}+(\mathit{v}\cdot \mathrm{\nabla })\mathit{v}+\mathrm{\nabla }\mathit{\varphi }+\mathrm{2}\mathbf{\Omega }\times \mathit{v}+{\displaystyle \frac{\mathrm{\nabla }P}{\mathit{\rho }}}=\mathrm{0},\\ & {\partial }_t\mathit{\rho }+\mathrm{\nabla }\cdot \left(\mathit{\rho }\mathit{v}\right)=\mathrm{0},\\ & {\partial }_{t}s+(\mathit{v}\cdot \mathrm{\nabla })s=\mathrm{0}.\end{array}\end{array}$$

Here, the usual notation is used, with s being entropy per unit mass, ϕ the geopotential and Ω an angular velocity vector. The pressure $P=P(\mathit{\alpha },s)$ is considered to be a function of the specific volume $\mathit{\alpha }=\mathrm{1}/\mathit{\rho }$ and entropy (to distinguish pressure from a conjugated momentum p to be introduced later, we denote pressure with a capital letter). In the Lagrangian coordinates, these equations reduce to a single equation

$$\begin{array}{}\text{(2)}& {\partial }_t^{\mathrm{2}}\mathit{\xi }+\mathrm{\nabla }\mathit{\varphi }+\mathrm{2}\mathbf{\Omega }\times {\partial }_t\mathit{\xi }+{\displaystyle \frac{\mathrm{\nabla }P}{\mathit{\rho }}}=\mathrm{0},\end{array}$$

where $\mathit{\xi }=\mathit{\xi }(t,\mathit{a}$) is the displacement of a fluid particle from its original location at a. The entropy, which for a given fluid particle is conserved, is determined by its initial spatial distribution s₀:

$$s=s_{\mathrm{0}}\left(\mathit{a}\right).$$

The density ρ in Eq. (2) follows from mass conservation and is given by the equation

$$\begin{array}{}\text{(3)}& \begin{array}{rl}\mathit{\rho }(t,\mathit{a})& ={\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right){\left|{\displaystyle \frac{\partial \left(\mathit{r}\right)}{\partial \left(\mathit{a}\right)}}\right|}^{-\mathrm{1}}={\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right){\left|{\displaystyle \frac{\partial (\mathit{a}+\mathit{\xi })}{\partial \left(\mathit{a}\right)}}\right|}^{-\mathrm{1}}\\ & ={\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right){\left|\mathrm{1}+{\displaystyle \frac{\partial \left(\mathit{\xi }\right)}{\partial \left(\mathit{a}\right)}}\right|}^{-\mathrm{1}},\end{array}\end{array}$$

where $\mathit{r}=\mathit{a}+\mathit{\xi }$ is the Cartesian coordinate of a fluid particle, | | denotes the determinant of the corresponding matrix and ρ₀(a) is the spatial distribution of density at t=0. Equation (2) represents Newton's second law. Note that the gradients in this equation are taken with respect to the Cartesian r rather than a coordinates.

The action A in the general case is defined as follows:

$$\begin{array}{}\text{(4)}& A=\underset{t_{\mathrm{0}}}{\overset{t_{\mathrm{1}}}{\int }}{L}_{\ast }(q_i,{\dot{q}}_i)\mathrm{d}t,\end{array}$$

where q_i is a set of arbitrary parameters characterizing the system state, and ${\dot{q}}_i$ denotes their time derivatives. The index i can be either discrete or continuous. The “star” index in L_∗ is introduced to distinguish the total Lagrangian L_∗ from its (spatial) density $L=\mathrm{d}{L}_{\ast }/\mathrm{d}\mathit{a}$, where da means an element of volume with respect to a coordinates. The least action principle

$$\begin{array}{}\text{(5)}& \mathit{\delta }A=\mathrm{0}\end{array}$$

results in the following (Euler–Lagrange) evolution equations:

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\displaystyle \frac{\partial L_{\ast }}{\partial {\dot{q}}_i}}-{\displaystyle \frac{\partial L_{\ast }}{\partial q_i}}=\mathrm{0}.\end{array}$$

We now demonstrate that Eq. (2) follows from LAP (Eq. 5) for

$$L_{\ast }(\mathit{\xi },{\partial }_t\mathit{\xi })=\int L(\mathit{\xi },{\partial }_t\mathit{\xi },\mathit{a})\mathrm{d}\mathit{a},$$

with the Lagrangian density L defined as follows:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}L(\mathit{\xi },{\partial }_t\mathit{\xi },\mathit{a})=& {\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)\mathit{\left\{}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\right({\partial }_t\mathit{\xi }{)}^{\mathrm{2}}-E(\mathit{\alpha },s_{\mathrm{0}}(\mathit{a}\left)\right)\\ & -g(\mathit{n}\cdot \mathit{\xi })-\mathbf{\Omega }\cdot ({\partial }_t\mathit{\xi }\times \mathit{\xi })\mathit{\}}.\end{array}\end{array}$$

In Eq. (7), E(α,s) is the internal energy of the dry air per unit mass, n is a unit vector directed upwards along the gradient of geopotential and g is its magnitude.

Let us calculate variation of the total energy with respect to ξ, taking into account that according to the basic thermodynamic identity $T\mathrm{d}s=\mathrm{d}E+P\mathrm{d}\mathit{\alpha }$, one has $P=-(\partial E/\partial \mathit{\alpha }{)}_{\mathrm{s}}$:

$$\begin{array}{rl}\mathit{\delta }\int {\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)E(\mathit{\alpha },s_{\mathrm{0}}(\mathit{a}\left)\right)\mathrm{d}\mathit{a}=& \int {\mathit{\rho }}_{\mathrm{0}}{\displaystyle \frac{\partial E}{\partial \mathit{\alpha }}}\mathit{\delta }\mathit{\alpha }\mathrm{d}\mathit{a}\\ & =-\int {\mathit{\rho }}_{\mathrm{0}}P\mathit{\delta }\left({\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)}}\left|{\displaystyle \frac{\partial \mathit{r}}{\partial \mathit{a}}}\right|\right)\mathrm{d}\mathit{a}\\ =& -\int P\sum _{i,j=\mathrm{1}}^{\mathrm{3}}{C}_{ij}{\displaystyle \frac{\partial }{\partial a_j}}\mathit{\delta }{\mathit{\xi }}_i\mathrm{d}\mathit{a}\\ =& -\int (\mathit{N}\cdot \mathit{\delta }\mathit{\xi })P\mathrm{d}\mathrm{\Sigma }\\ & +\int \sum _{i,j=\mathrm{1}}^{\mathrm{3}}{\displaystyle \frac{\partial P}{\partial a_j}}{C}_{ij}\mathit{\delta }{\mathit{\xi }}_i\mathrm{d}\mathit{a}.\end{array}$$

Here, C_ij is the cofactor of the (i,j)th entry of matrix $\partial \mathit{r}/\partial \mathit{a}$ (i.e. the determinant of this matrix with the ith row and jth column deleted multiplied by $(-\mathrm{1}{)}^{i+j}$). Integration by parts (i.e. use of the Gauss theorem) leads to appearance of the first (surface) term, with N being a unit outward normal to the boundary of the medium Σ. It is easy to make sure that $\sum _j\partial C_{ij}/\partial a_j=\mathrm{0}$; for this reason, the derivatives of C_ij in the equation above are absent. Considering that the matrix of cofactors transposed is proportional to the inverse matrix, one has

$$C_{ij}=\left|{\displaystyle \frac{\partial \mathit{r}}{\partial \mathit{a}}}\right|{\left({\left({\displaystyle \frac{\partial \mathit{r}}{\partial \mathit{a}}}\right)}^{-\mathrm{1}}\right)}_{ji}=\left|{\displaystyle \frac{\partial \mathit{r}}{\partial \mathit{a}}}\right|{\displaystyle \frac{\partial a_j}{\partial r_i}}.$$

Taking into account that according to Eq. (3), $\mathrm{|}\partial \mathit{r}/\partial \mathit{a}\mathrm{|}={\mathit{\rho }}_{\mathrm{0}}/\mathit{\rho }$, one finds

$$\sum _{j=\mathrm{1}}^{\mathrm{3}}{\displaystyle \frac{\partial P}{\partial a_j}}{C}_{ij}={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}}{\mathit{\rho }}}\sum _{j=\mathrm{1}}^{\mathrm{3}}{\displaystyle \frac{\partial P}{\partial a_j}}{\displaystyle \frac{\partial a_j}{\partial r_i}}={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}}{\mathit{\rho }}}{\displaystyle \frac{\partial P}{\partial r_i}},$$

where now P in the last equation above is considered to be a function of r rather than a. As a result, we obtain

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\mathit{\delta }\int {\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)E(\mathit{\alpha },s_{\mathrm{0}}(\mathit{a}\left)\right)\mathrm{d}\mathit{a}=& -\int (\mathit{N}\cdot \mathit{\delta }\mathit{\xi })P\mathrm{d}\mathrm{\Sigma }\\ & +\int {\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}}{\mathit{\rho }}}{\displaystyle \frac{\partial P}{\partial \mathit{r}}}\cdot \mathit{\delta }\mathit{\xi }\mathrm{d}\mathit{a}.\end{array}\end{array}$$

Now, calculating the variation of the action Eqs. (4) and (7) and integrating terms proportional to ∂_tδξ by parts with respect to time yields

$$\begin{array}{}\text{(9)}& \begin{array}{rl}\mathit{\delta }A=& -\int \mathrm{d}t\mathrm{d}\mathit{a}{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)({\partial }_t^{\mathrm{2}}\mathit{\xi }+g\mathit{n}+\mathrm{2}\mathbf{\Omega }\times {\partial }_t\mathit{\xi }\\ & +{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}{\displaystyle \frac{\partial P}{\partial \mathit{r}}})\cdot \mathit{\delta }\mathit{\xi }+\int (\mathit{N}\cdot \mathit{\delta }\mathit{\xi })P\mathrm{d}\mathrm{\Sigma }\mathrm{d}t.\end{array}\end{array}$$

We can see that the requirement δA=0 in Eq. (9) for internal points in fact coincides with Eq. (2). The internal energy of dry air E=C_VT in terms of the variables (α,s) is given by

$$\begin{array}{}\text{(10)}& E(\mathit{\alpha },s)={\displaystyle \frac{p_{\mathrm{00}}{\mathit{\alpha }}_{\mathrm{00}}^{\mathit{\gamma }}}{\mathit{\gamma }-\mathrm{1}}}{\mathit{\alpha }}^{\mathrm{1}-\mathit{\gamma }}{e}^{s/C_{\mathrm{V}}},\end{array}$$

where p₀₀ and α₀₀ are reference values of pressure and specific volume, and $\mathit{\gamma }=C_{\mathrm{P}}/C_{\mathrm{V}}$ is, as usual, the ratio of specific heats.

To derive a set of numerically accessible dynamical equations that adequately describe the evolution of the continuous atmosphere requires one additional standard step. One difficulty is that the left-hand side (LHS) of Eq. (6) in the discrete case will generally contain a mix of second derivatives of the discrete coordinates ${\ddot{q}}_i$ with different indices, and as they are not being resolved with respect to ${\ddot{q}}_i$, the resulting equations are ill-suited for numerical solution. This issue can be resolved by representing Eq. (6) in the Hamiltonian form. Namely, we introduce the momenta p_i according to the relation

$$\begin{array}{}\text{(11)}& p_i={\displaystyle \frac{\partial L_{\ast }}{\partial {\dot{q}}_i}}\end{array}$$

and express ${\dot{q}}_i$ from these equations as functions of q and p. From this point forward, the variable p will stand for conjugated momentum. We introduce the Hamiltonian $H_{\ast }(q,p)$ instead of the Lagrangian $L_{\ast }(q,\dot{q})$ according to the equation

$$\begin{array}{}\text{(12)}& H_{\ast }(q,p)=\sum _i{\dot{q}}_i{p}_i-L_{\ast }(q,\dot{q}),\end{array}$$

where all ${\dot{q}}_i$ values have been expressed as functions of q and p, as noted above. It is not difficult to show using Eqs. (11) and (12) that the following (Hamiltonian) equations hold:

$$\begin{array}{}\text{(13)}& {\dot{q}}_i={\displaystyle \frac{\partial H_{\ast }}{\partial p_i}},{\dot{p}}_i=-{\displaystyle \frac{\partial H_{\ast }}{\partial q_i}}.\end{array}$$

These expressions follow by applying LAP (Eq. 5) to

$$\begin{array}{}\text{(14)}& A=\underset{t_{\mathrm{0}}}{\overset{t_{\mathrm{1}}}{\int }}\left\{\sum _i{\dot{q}}_i{p}_i-H_{\ast }(q,p)\right\}\mathrm{d}t\end{array}$$

and varying the variables q_i and p_i independently. In what follows, we will only be using LAP in this form.

Substituting Eq. (7) into Eq. (11), we obtain

$$\begin{array}{}\text{(15)}& \mathit{p}(t,\mathit{a})={\displaystyle \frac{\partial L(\mathit{\xi },{\partial }_t\mathit{\xi },\mathit{a})}{\partial \left({\partial }_t\mathit{\xi }\right)}}={\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)({\partial }_t\mathit{\xi }+\mathbf{\Omega }\times \mathit{\xi }).\end{array}$$

Expressing ∂_tξ in terms of p and ξ and substituting the result into Eq. (12) after simple transformations for the density of the Hamiltonian yields

$$\begin{array}{}\text{(16)}& \begin{array}{rl}H(\mathit{\xi },\mathit{p};\mathit{a})=& {\displaystyle \frac{(\mathit{p}-{\mathit{\rho }}_{\mathrm{0}}(\mathit{a})\mathbf{\Omega }\times \mathit{\xi }{)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)}}\\ & +{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)E(\mathit{\alpha },s_{\mathrm{0}}(\mathit{a}\left)\right)+g{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)(\mathit{n}\cdot \mathit{\xi }).\end{array}\end{array}$$

The Hamiltonian equations (Eq. 13) read

$$\begin{array}{rl}{\partial }_t\mathit{\xi }=& {\displaystyle \frac{\mathit{\delta }H}{\mathit{\delta }\mathit{p}}}={\displaystyle \frac{\mathit{p}-{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)\mathbf{\Omega }\times \mathit{\xi }}{{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)}}\\ {\partial }_t\mathit{p}=& -{\displaystyle \frac{\mathit{\delta }H}{\mathit{\delta }\mathit{\xi }}}=(\mathit{p}-{\mathit{\rho }}_{\mathrm{0}}(\mathit{a})\mathbf{\Omega }\times \mathit{\xi })\times \mathbf{\Omega }-g{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)\mathit{n}\\ & -{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)}{\mathit{\rho }}}{\displaystyle \frac{\partial P}{\partial \mathit{r}}}.\end{array}$$

By differentiating the first of these equations with respect to time and inserting ∂_tp from the result using the second equation, we make sure that the result coincides in fact with Eq. (2).

Finally, the expression in Eq. (14) for the action for the continuous atmosphere reduces to

$$\begin{array}{}\text{(17)}& \begin{array}{rl}A=& \underset{t_{\mathrm{0}}}{\overset{t_{\mathrm{1}}}{\int }}\mathrm{d}t\int \mathrm{d}\mathit{a}\mathit{\{}\mathit{p}\cdot {\partial }_t\mathit{\xi }-{\displaystyle \frac{(\mathit{p}-{\mathit{\rho }}_{\mathrm{0}}[\mathbf{\Omega },\mathit{\xi }]{)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)}}\\ & -{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)E(\mathit{\alpha },s_{\mathrm{0}}(\mathit{a}\left)\right)-g{\mathit{\rho }}_{\mathrm{0}}\left(\mathit{a}\right)(\mathit{n}\cdot \mathit{\xi })\mathit{\}}.\end{array}\end{array}$$

3 The action for a discrete atmospheric model

We now need to select a set of discrete parameters that represent a continuous atmosphere and a way of interpolating these parameters to an arbitrary spatial point. The model that will be used here is as follows. We split the region of interest into a set of unstructured connected tetrahedra that share vertices, edges and faces. We select values for the displacements ξ and momenta p, as well as the density ρ₀ and specific entropy s₀, at the vertices, which define a set of discrete parameters that represent the continuous atmosphere. To calculate corresponding parameters at an arbitrary point within each tetrahedron, we will be using linear interpolation. We note that four values of a parameter at the four vertices of a tetrahedron completely determine its linear interpolation within the tetrahedron. The piecewise-linear interpolation ensures a globally continuous representation of the corresponding fields throughout the region. Derivatives along the faces of tetrahedra are also continuous; however, derivatives across the faces experience jumps, which for a sufficiently dense set of tetrahedra are negligible. Let us also note that such interpolation ensures calculation of the action to the accuracy of the square of the ratio of a linear size of the tetrahedra to a spatial scale of variations of atmospheric parameters.

We can now approximate the action A by $\stackrel{\mathrm{̃}}{A}$, where

$$\begin{array}{}\text{(18)}& A\approx \stackrel{\mathrm{̃}}{A}=\sum _T{A}_T,\end{array}$$

where the index T stands for an individual tetrahedron, and the summation aggregates the contribution from all tetrahedra. The action A_T is calculated according to Eq. (17), where the integral is over the volume occupied by the Tth tetrahedron.

Let us consider the first term $\mathit{p}\cdot {\partial }_t\mathit{\xi }$ in Eq. (17). The following relation can be shown to hold true for two linear functions of coordinates u(a) and v(a) defined within a tetrahedron by linear approximations based on their values u_i, v_i and $i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}$ at the vertices of the tetrahedron:

$$\begin{array}{}\text{(19)}& \begin{array}{rl}\underset{T}{\int }u\left(\mathit{a}\right)v\left(\mathit{a}\right)\mathrm{d}\mathit{a}=& {\displaystyle \frac{\mathrm{|}{V}_T\mathrm{|}}{\mathrm{4}}}(\sum _{i=\mathrm{1}}^{\mathrm{4}}{u}_i{v}_i\\ & -{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{i,j=\mathrm{1}}^{\mathrm{4}}(u_i-u_j)(v_i-v_j)).\end{array}\end{array}$$

Here |V_T| is the tetrahedron's volume. The same equation also holds in the 2D case, with the $\mathrm{1}/\mathrm{4}$ factor replaced by $\mathrm{1}/\mathrm{3}$ and summations proceeding from 1 to 3. For smooth fields, the differences in the second term in the right-hand side (RHS) of Eq. (19) will be proportional to the ratio of the linear size of the tetrahedron to the characteristic scale of the parameter's variation, and the magnitude of the entire second term will be proportional to the square of this ratio and can generally be neglected when compared to the first term in Eq. (19). We then find

$$\begin{array}{}\text{(20)}& \underset{T}{\int }\mathit{p}\cdot {\partial }_t\mathit{\xi }\mathrm{d}\mathit{a}\approx {\displaystyle \frac{\mathrm{|}{V}_T\mathrm{|}}{\mathrm{4}}}\sum _{i=\mathrm{1}}^{\mathrm{4}}{\mathit{p}}_i\cdot {\partial }_t{\mathit{\xi }}_i.\end{array}$$

Here and below, vector symbols (bold italic) indicate 3D vectors, and indices correspond to vertices. Dots between vectors denote scalar products with respect to 3D vector coordinates, correspondingly. We note, however, that the neglected term in Eq. (19) can be retained by replacing (to a first approximation) the differences ${\partial }_t{\mathit{\xi }}_i-{\partial }_t{\mathit{\xi }}_j$ in Eq. (19) by $\partial H/\partial {\mathit{p}}_i-\partial H/\partial {\mathit{p}}_j$. This will result in the following modification to the Hamiltonian density in Eq. (16) within the corresponding tetrahedron:

$$H(\mathit{\xi },\mathit{p};\mathit{a})\to H(\mathit{\xi },\mathit{p};\mathit{a})-{\displaystyle \frac{\mathrm{1}}{\mathrm{8}}}\sum _{i,j=\mathrm{1}}^{\mathrm{4}}({\mathit{p}}_i-{\mathit{p}}_j)\cdot \left({\displaystyle \frac{\partial H}{\partial {\mathit{p}}_i}}-{\displaystyle \frac{\partial H}{\partial {\mathit{p}}_i}}\right).$$

The transition from a continuous to discrete description of the mechanical system based on the approximation of action, which is pursued here, differs from the more customary approximation of a continuous Hamiltonian by a discrete analogue (Salmon, 1983).

Using Eq. (20) we can represent the action as

$$\begin{array}{}\text{(21)}& \begin{array}{rl}\stackrel{\mathrm{̃}}{A}=& \underset{t_{\mathrm{0}}}{\overset{t_{\mathrm{1}}}{\int }}\mathrm{d}t\sum _T\mathrm{|}{V}_T\mathrm{|}({\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\sum _{n\left(T\right)}{\mathit{p}}_{n\left(T\right)}\cdot {\partial }_t{\mathit{\xi }}_{n\left(T\right)}\\ & -{\stackrel{\mathrm{̃}}{H}}_T({\mathit{\xi }}_{n\left(T\right)},{\mathit{p}}_{n\left(T\right)})),\end{array}\end{array}$$

where

$$\begin{array}{}\text{(22)}& {\stackrel{\mathrm{̃}}{H}}_T({\mathit{\xi }}_{n\left(T\right)},{\mathit{p}}_{n\left(T\right)})={\displaystyle \frac{\mathrm{1}}{\mathrm{|}{V}_T\mathrm{|}}}\underset{T}{\int }H(\mathit{\xi },\mathit{p};\mathit{a})d\mathit{a}\end{array}$$

is the Hamiltonian in Eq. (16) integrated over the Tth tetrahedron and normalized by its volume. ${\stackrel{\mathrm{̃}}{H}}_T$ is a function of shifts and momenta at the vertices of the tetrahedron ξ_n(T) and p_n(T), where n(T) stands for indices of the set of four vertices of the Tth tetrahedron. In Eq. (21), we now replace the summation over tetrahedra with a summation over vertices and represent it in the following form:

$$\begin{array}{}\text{(23)}& \begin{array}{rl}\stackrel{\mathrm{̃}}{A}=& \underset{t_{\mathrm{0}}}{\overset{t_{\mathrm{1}}}{\int }}\mathrm{d}t\sum _k(v_k{\mathit{p}}_k\cdot {\partial }_t{\mathit{\xi }}_k\\ & -\sum _{\mathit{\tau }\subset T\left(k\right)}\mathrm{|}{V}_{\mathit{\tau }}\mathrm{|}{\stackrel{\mathrm{̃}}{H}}_{\mathit{\tau }}({\mathit{\xi }}_{n\left(\mathit{\tau }\right)},{\mathit{p}}_{n\left(\mathit{\tau }\right)})).\end{array}\end{array}$$

Here, T(k) represents indices of the tetrahedra that contain the vertex with index k, and the summation within the outward parentheses in Eq. (23) aggregates the contribution over all such tetrahedra. The parameter v_k is a quarter of the sum of their volumes:

$$\begin{array}{}\text{(24)}& v_k={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\sum _{\mathit{\tau }\subset T\left(k\right)}\mathrm{|}{V}_{\mathit{\tau }}\mathrm{|}.\end{array}$$

Equation (23) describes an approximation of the action for a continuous atmosphere in terms of a finite set of discrete parameters. We can now write the equation for the evolution of these parameters by minimizing $\stackrel{\mathrm{̃}}{A}$ in Eq. (23) as

$$\begin{array}{}\text{(25)}& \begin{array}{rl}{\partial }_t{\mathit{\xi }}_k& ={\displaystyle \frac{\mathrm{1}}{v_k}}\sum _{\mathit{\tau }\subset T\left(k\right)}\mathrm{|}{V}_{\mathit{\tau }}\mathrm{|}{\displaystyle \frac{\partial }{\partial {\mathit{p}}_k}}{\stackrel{\mathrm{̃}}{H}}_{\mathit{\tau }}({\mathit{\xi }}_{n\left(\mathit{\tau }\right)},{\mathit{p}}_{n\left(\mathit{\tau }\right)}),\\ {\partial }_t{\mathit{p}}_k& =-{\displaystyle \frac{\mathrm{1}}{v_k}}\sum _{\mathit{\tau }\subset T\left(k\right)}\mathrm{|}{V}_{\mathit{\tau }}\mathrm{|}{\displaystyle \frac{\partial }{\partial {\mathit{\xi }}_k}}{\stackrel{\mathrm{̃}}{H}}_{\mathit{\tau }}({\mathit{\xi }}_{n\left(\mathit{\tau }\right)},{\mathit{p}}_{n\left(\mathit{\tau }\right)}).\end{array}\end{array}$$

Note that the action in Eq. (23) can be cast precisely into the form in Eq. (14) by rescaling coordinates and momenta, thus making the corresponding system explicitly Hamiltonian, although this step is not needed here. Since the approximate action is invariant with respect to shifts in time, the approximate energy is conserved. Similarly, if the exact action is invariant with respect to geometrical transformations like shifts in space or rotations, the approximate action will inherit this property along with corresponding conservation laws. In this case conservation will be exact; however, the conserved values will be calculated approximately.

Equation (25) can be solved numerically using a suitable integration scheme (e.g. Runge–Kutta). There are also time-integration schemes that conserve energy exactly (namely symplectic (Eldred et al., 2019) and variational (Mardsen and West, 2001; Lew et al., 2003)).

3.1 Lagrangian reassignment

To be able to repeat the time step, we have to reassign values of momenta p_k at corresponding vertices, whose locations a_k are fixed in space. The familiar procedure of the Lagrangian reassignment (a.k.a. semi-Lagrangian advection, Lagrangian remapping, etc.) is detailed in this subsection in conjunction with the linear interpolation employed in this work. We emphasize that ξ_k and p_k in Eq. (25) are Lagrangian coordinates, and p_k(Δt) is the momentum of a fluid particle which at t=Δt is located at a point ${\mathit{r}}_k={\mathit{a}}_k+{\mathit{\xi }}_k\left(\mathrm{\Delta }t\right)$ and not at a_k. For this reason, we have to first determine which particle moved to a_k at t=Δt and then calculate its momentum using the forward operator (i.e. linear interpolation). This value will be an initial condition for p_k in Eq. (25) for the next time step. The initial values of entropy and passive tracers will also correspond to the fluid particle that moved to a_k. These should be reassigned as well. The initial values of shifts are always ξ_k=0. By making these reassignments, we are essentially returning to the Eulerian description of fluid motion.

To determine the initial location of a fluid particle that arrived at a point R at a time t=Δt, we proceed as follows. The position of an arbitrary point within a tetrahedron can be expressed as follows:

$$\begin{array}{}\text{(26)}& \mathit{r}={\mathit{a}}_{\mathrm{4}}+({\mathit{a}}_{\mathrm{1}}-{\mathit{a}}_{\mathrm{4}}){\mathit{\tau }}_{\mathrm{1}}+({\mathit{a}}_{\mathrm{2}}-{\mathit{a}}_{\mathrm{1}}){\mathit{\tau }}_{\mathrm{2}}+({\mathit{a}}_{\mathrm{3}}-{\mathit{a}}_{\mathrm{2}}){\mathit{\tau }}_{\mathrm{3}},\end{array}$$

where a_i denotes the Cartesian coordinates of the ith vertex of the tetrahedron, and the fourth vertex was arbitrarily selected in Eq. (26) as a base point. For the point r to be within the tetrahedron, the scalar dimensionless parameters τ_i (which have nothing to do with τ in Eqs. (24) and (25)) should satisfy

$$\begin{array}{}\text{(27)}& \mathrm{1}>{\mathit{\tau }}_{\mathrm{1}}>{\mathit{\tau }}_{\mathrm{2}}>{\mathit{\tau }}_{\mathrm{3}}>\mathrm{0}.\end{array}$$

Due to the assumption of a linear dependence of the shifts ξ on the Cartesian coordinates within a tetrahedron, the fluid particle located at r at t=0 at the end of a time step at t=Δt will experience a shift given by an expression similar to Eq. (26), that is

$$\begin{array}{}\text{(28)}& \mathit{\xi }={\mathit{\xi }}_{\mathrm{4}}+({\mathit{\xi }}_{\mathrm{1}}-{\mathit{\xi }}_{\mathrm{4}}){\mathit{\tau }}_{\mathrm{1}}+({\mathit{\xi }}_{\mathrm{2}}-{\mathit{\xi }}_{\mathrm{1}}){\mathit{\tau }}_{\mathrm{2}}+({\mathit{\xi }}_{\mathrm{3}}-{\mathit{\xi }}_{\mathrm{2}}){\mathit{\tau }}_{\mathrm{3}},\end{array}$$

where ξ_i, $i=\mathrm{1},\mathrm{\dots },\mathrm{4}$ are shifts of fluid particles located at corresponding vertices at t=0; these shifts are known as a result of numerical integration of Eq. (25). The requirement of the fluid particle to translate from a point r to a point R is given by

$$\mathit{r}+\mathit{\xi }=\mathit{R}.$$

Substituting into this equation Eqs. (26) and (28), we obtain the following vector linear equation with respect to the parameters τ_i :

$$\begin{array}{}\text{(29)}& \sum _{i=\mathrm{1}}^{\mathrm{3}}({\mathit{a}}_i-{\mathit{a}}_{\mathrm{4}}+{\mathit{\xi }}_i-{\mathit{\xi }}_{\mathrm{4}}){\mathit{\tau }}_i=\mathit{R}-{\mathit{a}}_{\mathrm{4}}-{\mathit{\xi }}_{\mathrm{4}}.\end{array}$$

The fluid particle can in principle arrive at the kth vertex from any tetrahedron from the set T(k); however, the condition in Eq. (27) selects the appropriate tetrahedron.

The existence and uniqueness (non-degeneracy) of solutions to Eq. (29) may be explained as follows. Let us consider the trajectories of fluid particles. The fluid particle that at t=0 was located at the vertex with coordinates a_i at a later moment of time t will be located at a point ${\mathit{r}}_i\left(t\right)={\mathit{a}}_i+{\mathit{\xi }}_i\left(t\right)$. Points r_i form vertices of a shifted tetrahedron onto which the initial tetrahedron is mapped. Note that shifts ξ of the fluid particles inside a tetrahedron are assumed to be linear functions of the shifts of the fluid particles located at the vertices of the tetrahedron: this is our basic (linear) approximation of the forward operator (see the first paragraph of Sect. 3). Thus, the initial tetrahedron with the vertices at the points a_i linearly (more precisely, affinely) mapped onto a shifted tetrahedron with vertices at r_i; the transformation is linear regardless of the trajectories of the fluid particles, which started from the vertices a_i being linear or curved. In particular, faces and edges of the initial tetrahedron are mapped onto corresponding faces and edges of the shifted tetrahedron. Since shifts of the internal points of the tetrahedron are linear functions of coordinates, the Jacobian of the linear transformation of the initial tetrahedron within it is constant (the constants for different tetrahedrons are, of course, also different, and they depend on time t). Thus, piecewise linearity of the forward operator ensures that the mapping of the whole initial volume onto the shifted volume is also piecewise linear, and the mapping is one to one provided that neither tetrahedron in the course of evolution degenerates (i.e. tetrahedra volumes never become zero). The latter is achieved by adopting a Courant-limited time step based on the fastest wave mode that the equations admit (here, the sound speed), which also ensures that time integration errors remain small. Non-degeneracy of the initial tetrahedrons can be checked easily, since trajectories of the fluid particles at the vertices are calculated in the course of numerical integration.

The value of any parameter within a tetrahedron at the end of a time step is given by an expression quite similar to Eq. (28). For example, the momentum at a time t=Δt at a vertex with Cartesian coordinate R is given by

$$\begin{array}{}\text{(30)}& \mathit{p}={\mathit{p}}_{\mathrm{4}}+({\mathit{p}}_{\mathrm{1}}-{\mathit{p}}_{\mathrm{4}}){\mathit{\tau }}_{\mathrm{1}}+({\mathit{p}}_{\mathrm{2}}-{\mathit{p}}_{\mathrm{1}}){\mathit{\tau }}_{\mathrm{2}}+({\mathit{p}}_{\mathrm{3}}-{\mathit{p}}_{\mathrm{2}}){\mathit{\tau }}_{\mathrm{3}},\end{array}$$

where p_i=p_i(Δt) denotes the momenta which are also known as a result of numerical integration of Eq. (25). The parameters τ_i in Eq. (30) follow from the solution of Eq. (29). The resulting p in Eq. (30) is the momentum, which has to be reassigned to corresponding vertex as an initial condition for the next time step. The specific entropy at the vertices should also be redefined according to Eq. (30), where now the values of s₀ at t=0 should be substituted for p_i (since the entropy of the fluid particle is conserved). All other passive tracers should be similarly redefined. The value of the density ρ₀ at the kth vertex should be redefined using Eq. (3) with respect to the same tetrahedron and the same fluid particles that were used for recalculating the momentum and entropy (i.e. with the same τ_i following from Eq. 29).

3.2 Local Hamiltonian calculation

We consider now the calculation of the Hamiltonian $\stackrel{\mathrm{̃}}{H}$, which forms the basis of the numerical model. We note that Eq. (25) describes the evolution of the model parameters and includes the derivatives of $\stackrel{\mathrm{̃}}{H}$. For simplicity, here, we assign the indices $n=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}$ to the vertices of a tetrahedron. We now recast the integration over a in Eq. (2) into an integration over the dimensionless parameters ${\mathit{\tau }}_{\mathrm{1},\mathrm{2},\mathrm{3}}$ according to Eq. (26). The functions ξ(a), p(a), ρ₀(a) and s₀(a) are calculated according to the selected forward operator, i.e. by linear approximation, quite similar to Eqs. (28) and (30):

$$\begin{array}{}\text{(31)}& f\left({\mathit{\tau }}_i\right)=f_{\mathrm{4}}+(f_{\mathrm{1}}-f_{\mathrm{4}}){\mathit{\tau }}_{\mathrm{1}}+(f_{\mathrm{2}}-f_{\mathrm{4}}){\mathit{\tau }}_{\mathrm{2}}+(f_{\mathrm{3}}-f_{\mathrm{4}}){\mathit{\tau }}_{\mathrm{3}},\end{array}$$

where f is any parameter (vector or scalar), and f_n is a value of f at the nth vertex.

According to Eq. (25) we have

$$\begin{array}{}\text{(32)}& {\stackrel{\mathrm{̃}}{H}}_T({\mathit{\xi }}_n,{\mathit{p}}_n)=\mathrm{6}\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}\mathrm{d}{\mathit{\tau }}_{\mathrm{1}}\underset{\mathrm{0}}{\overset{{\mathit{\tau }}_{\mathrm{1}}}{\int }}\mathrm{d}{\mathit{\tau }}_{\mathrm{2}}\underset{\mathrm{0}}{\overset{{\mathit{\tau }}_{\mathrm{2}}}{\int }}\mathrm{d}{\mathit{\tau }}_{\mathrm{3}}H\left(\mathit{\xi }\right({\mathit{\tau }}_n),\mathit{p}({\mathit{\tau }}_n);{\mathit{\tau }}_n),\end{array}$$

where H is given by Eq. (16) and ξ(τ_n) and p(τ_n) by Eq. (31). Afterwards, the LHS of Eq. (32) becomes a function of the values of the displacements ξ and momenta p at the vertices of the tetrahedron. Note that since ξ is a linear function of coordinates a, the Jacobian in Eq. (3) is a constant independent of a, and we can write

$$\mathit{\alpha }\left({\mathit{\tau }}_n\right)={\displaystyle \frac{{\mathrm{\Delta }}_{\mathrm{0}}\left({\mathit{\xi }}_n\right)}{{\mathit{\rho }}_{\mathrm{0}}\left({\mathit{\tau }}_n\right)}},$$

where Δ₀(ξ_n) is the value of the Jacobian. The internal energy in Eq. (16) can then be expressed as

$$\begin{array}{}\text{(33)}& \begin{array}{rl}{\mathit{\rho }}_{\mathrm{0}}E(\mathit{\alpha },s_{\mathrm{0}})=& {\displaystyle \frac{p_{\mathrm{00}}{\mathit{\alpha }}_{\mathrm{00}}^{\mathit{\gamma }}}{\mathit{\gamma }-\mathrm{1}}}\left({\mathrm{\Delta }}_{\mathrm{0}}\right(\mathit{\xi }\left){)}^{\mathrm{1}-\mathit{\gamma }}\right({\mathit{\rho }}_{\mathrm{0}}\left({\mathit{\tau }}_n\right){)}^{\mathit{\gamma }}\\ & \times \exp \left({\displaystyle \frac{s_{\mathrm{0}}\left({\mathit{\tau }}_n\right)}{C_{\mathrm{V}}}}\right).\end{array}\end{array}$$

To calculate the integral in Eq. (32) related to the internal energy term, we note that variations of density within a tetrahedron are generally small and set

$$\begin{array}{}\text{(34)}& \begin{array}{rl}\left({\mathit{\rho }}_{\mathrm{0}}\right({\mathit{\tau }}_n){)}^{\mathit{\gamma }}=& {\mathit{\rho }}_{\mathrm{4}}^{\mathit{\gamma }}{\left(\mathrm{1}+\left(\sum _{n=\mathrm{1}}^{\mathrm{3}}{\mathit{\beta }}_n{\mathit{\tau }}_n\right)\right)}^{\mathit{\gamma }}\\ =& {\mathit{\rho }}_{\mathrm{4}}^{\mathit{\gamma }}\left(\mathrm{1}+\mathit{\gamma }\left(\sum _{n=\mathrm{1}}^{\mathrm{3}}{\mathit{\beta }}_n{\mathit{\tau }}_n\right)\right.\\ & \left.+{\displaystyle \frac{\mathit{\gamma }(\mathit{\gamma }-\mathrm{1})}{\mathrm{2}}}{\left(\sum _{n=\mathrm{1}}^{\mathrm{3}}{\mathit{\beta }}_n{\mathit{\tau }}_n\right)}^{\mathrm{2}}+\mathrm{\dots }\right),\end{array}\end{array}$$

where the factors

$$\begin{array}{}\text{(35)}& {\mathit{\beta }}_n={\displaystyle \frac{{\mathit{\rho }}_n-{\mathit{\rho }}_{\mathrm{4}}}{{\mathit{\rho }}_{\mathrm{4}}}}\end{array}$$

are also small, so that one only needs to retain the first few expansion terms in Eq. (34). One can similarly expand the exponential term in Eq. (33) into a power series. In this case calculation of the integral in Eq. (32) with respect to the internal energy term also reduces to an integration of polynomials of ${\mathit{\tau }}_{\mathrm{1},\mathrm{2},\mathrm{3}}$. Alternatively, one can leave the exponential term in Eq. (33) as is since the exponent is a linear function of ${\mathit{\tau }}_{\mathrm{1},\mathrm{2},\mathrm{3}}$, and integrals of products of polynomials and exponentials can be calculated analytically nearly as easily as integrals of polynomials. In the first term in the RHS of Eq. (16) (the kinetic energy), we also expand $\mathrm{1}/{\mathit{\rho }}_{\mathrm{0}}\left({\mathit{\tau }}_i\right)$ according to Eq. (34), where now in place of γ we substitute −1. Then, the integrations over ${\mathit{\tau }}_{\mathrm{1},\mathrm{2},\mathrm{3}}$ in this term also reduce to an integration of polynomials, and this is done analytically.

Now, we consider boundary conditions that follow from LAP. They are due to the last (surface) term in Eq. (9) and require that at the boundaries either the pressure or (N,δξ) is zero. Thus, without restrictions on the variations of shifts of the boundary points, the pressure at the boundary should be zero. Such a boundary condition can be applied reasonably to the top of the atmosphere (the issue of an absorbing layer is beyond the scope of this paper) but is unacceptable elsewhere. For such boundary points, we will assume that both the shifts ξ_k and momenta p_k are prescribed functions of time so that δξ_k=0. Equations for the corresponding k are excluded from the set in Eq. (25). Note that p and ξ are related through Eq. (15), and it is sufficient to prescribe a time dependence to only one or the other. In particular, at the bottom of the atmosphere, one can use the no-slip boundary condition ξ=0. To introduce different boundary conditions, one would need to add corresponding terms to the expression for the action.

Our numerical approach proceeds as follows. We introduce an array of tendencies (i.e. the time derivatives ∂_tξ_k, ∂_tp_k) with the total number of columns equal to the total number of vertices – one column per vertex. To calculate the RHS of the evolution equations in Eq. (25), we initiate a loop not over vertices but over tetrahedra. After calculating the derivatives $\partial {\stackrel{\mathrm{̃}}{H}}_{\mathit{\tau }}/\partial {\mathit{p}}_k$ and $\partial {\stackrel{\mathrm{̃}}{H}}_{\mathit{\tau }}/\partial {\mathit{\xi }}_k$ for all four vertices of a particular tetrahedron (which results in eight vectors with a total of 24 scalar parameters), we add/subtract the result to/from the tendencies being accumulated in the corresponding columns of the tendencies array. After all the tetrahedra are accounted for, the RHS of Eq. (25) will appear automatically. To execute this procedure, we also introduce an integer array with the same number of columns, with each column containing four indices of vertices belonging to a corresponding tetrahedron.

The algorithm under consideration easily allows us to modify the set of tetrahedra during simulations. If after a time step one finds that in a particular region spatial resolution should be increased, the corresponding tetrahedra are split into two. Each split tetrahedron is flagged, and two new tetrahedra are added. This operation can be repeated as many times as necessary. Similarly, previously split tetrahedra can be recombined into larger ones by reversing the process. The evolution is then calculated with respect to the modified set of tetrahedra.

4 A numerical example

The algorithm under consideration was tested for a 2D case for simplicity. The Hamiltonian structure can be introduced into the hydrodynamics in many different ways (Salmon, 1988), and the formulation used in this section is significantly different from the one used in Sects. 2 and 3. It is important, however, that the essence of the approach that is advocated in this paper is still the same: approximation of the action using linear interpolation of canonical variables within corresponding simplexes. In the 2D case tetrahedra are replaced by triangles and volumes by corresponding areas.

The following formulation was used in this section:

$$\begin{array}{}\text{(36)}& H=\int \mathrm{d}V\mathit{\rho }\left[{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{v}}^{\mathrm{2}}+gz+E(\mathit{\rho },s)+\mathrm{\Psi }\left(s\right)\right],\end{array}$$

where

$$\begin{array}{}\text{(37)}& \mathit{v}=\mathrm{\nabla }\mathit{\phi }-{\displaystyle \frac{\mathit{\lambda }}{\mathit{\rho }}}\mathrm{\nabla }s\end{array}$$

is velocity; ρ and s are the density and specific entropy, respectively, which play the role of coordinates; and φ and λ are conjugated momenta, which do not have a direct physical interpretation. A gauge function Ψ(s) is chosen to ensure hydrostatic equilibrium for the corresponding model of the atmosphere. The Hamiltonian (Eq. 36) was suggested in Goncharov et al. (1976), where the function Ψ(s) corresponded to the isothermal atmosphere. Here, this function was chosen for the more realistic case of an atmosphere with a constant temperature gradient:

$$\begin{array}{}\text{(38)}& T\left(z\right)=T_{\mathrm{00}}\left(\mathrm{1}-{\displaystyle \frac{z}{H}}\right).\end{array}$$

In this case, one sets

$$\begin{array}{}\text{(39)}& \mathrm{\Psi }\left(s\right)=-gH+(gH-C_{\mathrm{P}}{T}_{\mathrm{00}})\exp \left(-{\displaystyle \frac{s}{{\mathit{\beta }}_{\mathrm{0}}{C}_{\mathrm{V}}}}\right),\end{array}$$

where

$${\mathit{\beta }}_{\mathrm{0}}={\displaystyle \frac{gH}{C_v{T}_{\mathrm{00}}}}-\mathit{\gamma }.$$

The governing equations for the continuous case are as follows:

$$\begin{array}{}\text{(40)}& \begin{array}{rl}& {\partial }_t\mathit{\rho }={\displaystyle \frac{\mathit{\delta }H}{\mathit{\delta }\mathit{\phi }}}=-\mathrm{\nabla }\left(\mathit{\rho }\mathit{v}\right),\\ & {\partial }_t\mathit{\phi }=-{\displaystyle \frac{\mathit{\delta }H}{\mathit{\delta }\mathit{\rho }}}=-\mathit{v}\mathrm{\nabla }\mathit{\phi }+{\displaystyle \frac{{\mathit{v}}^{\mathrm{2}}}{\mathrm{2}}}-gz-{\left({\displaystyle \frac{\partial \mathit{\rho }E}{\partial \mathit{\rho }}}\right)}_{\mathrm{s}}-\mathrm{\Psi }\left(s\right),\\ & {\partial }_{t}s={\displaystyle \frac{\mathit{\delta }H}{\mathit{\delta }\mathit{\lambda }}}=-\mathit{v}\mathrm{\nabla }s,\\ & {\partial }_t\mathit{\lambda }=-{\displaystyle \frac{\mathit{\delta }H}{\mathit{\delta }s}}=-\mathrm{\nabla }\left(\mathit{\lambda }\mathit{v}\right)-\mathit{\rho }T-\mathit{\rho }{\mathrm{\Psi }}^{\prime }\left(s\right).\end{array}\end{array}$$

Similar to the approach presented in the previous sections, we split the atmosphere into a set of triangles and linearly interpolate all four prognostic variables $(\mathit{\rho },s,\mathit{\phi },\mathit{\lambda })$ within the triangles. The approximation in Eq. (20) was used for the action, where the factor of $\mathrm{1}/\mathrm{4}$ was replaced by $\mathrm{1}/\mathrm{3}$ and the volume by the area. The resulting discrete evolution equations are quite similar to Eq. (25) and are as follows:

$$\begin{array}{}\text{(41)}& \begin{array}{rl}& {\partial }_t{\mathit{\rho }}_k={\displaystyle \frac{\mathrm{1}}{{\mathit{\sigma }}_k}}\sum _{\mathit{\chi }\subset T\left(k\right)}\mathrm{|}{\mathrm{\Sigma }}_{\mathit{\chi }}\mathrm{|}{\displaystyle \frac{\partial {\stackrel{\mathrm{̃}}{H}}_{\mathit{\chi }}}{\partial {\mathit{\phi }}_k}},\\ & {\partial }_t{\mathit{\phi }}_k=-{\displaystyle \frac{\mathrm{1}}{{\mathit{\sigma }}_k}}\sum _{\mathit{\chi }\subset T\left(k\right)}\mathrm{|}{\mathrm{\Sigma }}_{\mathit{\chi }}\mathrm{|}{\displaystyle \frac{\partial {\stackrel{\mathrm{̃}}{H}}_{\mathit{\chi }}}{\partial {\mathit{\rho }}_k}},\\ & {\partial }_t{s}_k={\displaystyle \frac{\mathrm{1}}{{\mathit{\sigma }}_k}}\sum _{\mathit{\chi }\subset T\left(k\right)}\mathrm{|}{\mathrm{\Sigma }}_{\mathit{\chi }}\mathrm{|}{\displaystyle \frac{\partial {\stackrel{\mathrm{̃}}{H}}_{\mathit{\chi }}}{\partial {\mathit{\lambda }}_k}},\\ & {\partial }_t{\mathit{\lambda }}_k=-{\displaystyle \frac{\mathrm{1}}{{\mathit{\sigma }}_k}}\sum _{\mathit{\chi }\subset T\left(k\right)}\mathrm{|}{\mathrm{\Sigma }}_{\mathit{\chi }}\mathrm{|}{\displaystyle \frac{\partial {\stackrel{\mathrm{̃}}{H}}_{\mathit{\chi }}}{\partial s_k}},\end{array}\end{array}$$

where now

$$\begin{array}{}\text{(42)}& \begin{array}{rl}{\stackrel{\mathrm{̃}}{H}}_{\mathit{\chi }}({\mathit{\rho }}_n,s_n,{\mathit{\phi }}_n,{\mathit{\lambda }}_n)=& \mathrm{2}\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}\mathrm{d}{\mathit{\tau }}_{\mathrm{1}}\underset{\mathrm{0}}{\overset{{\mathit{\tau }}_{\mathrm{1}}}{\int }}\mathrm{d}{\mathit{\tau }}_{\mathrm{2}}\\ & \times H\left(\mathit{\rho }\right({\mathit{\tau }}_n),s({\mathit{\tau }}_n),\mathit{\phi }({\mathit{\tau }}_n),\mathit{\lambda }({\mathit{\tau }}_n);{\mathit{\tau }}_n).\end{array}\end{array}$$

Here, H is given by Eq. (36), and χ,T(k) corresponds to triangles instead of tetrahedra with

$${\mathit{\sigma }}_k={\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}\sum _{\mathit{\chi }\subset T\left(k\right)}\mathrm{|}{\mathrm{\Sigma }}_{\mathit{\chi }}\mathrm{|},$$

where |Σ_χ| represents the area of the χth triangle.

We note that the Hamiltonian in Eq. (36) can be applied to the 3D case as well. For this case, however, we only have two free parameters φ and λ to represent the velocity field in Eq. (37), and this is generally insufficient. This problem can be resolved by introducing two additional parameters into the representation for the velocity in Eq. (37):

$$\begin{array}{}\text{(43)}& \mathit{v}=\mathrm{\nabla }\mathit{\phi }-{\displaystyle \frac{\mathit{\lambda }}{\mathit{\rho }}}\mathrm{\nabla }s+\mathit{\zeta }\mathrm{\nabla }\mathit{\mu }.\end{array}$$

The form of the Hamiltonian in Eq. (36) and the procedure for calculating the action do not change, and another pair of equations needs to be added to Eq. (40) that correspond to the conservation of ζ and μ along the trajectories of fluid particles. Still, the Hamiltonian in Eq. (16) seems to be a better option.

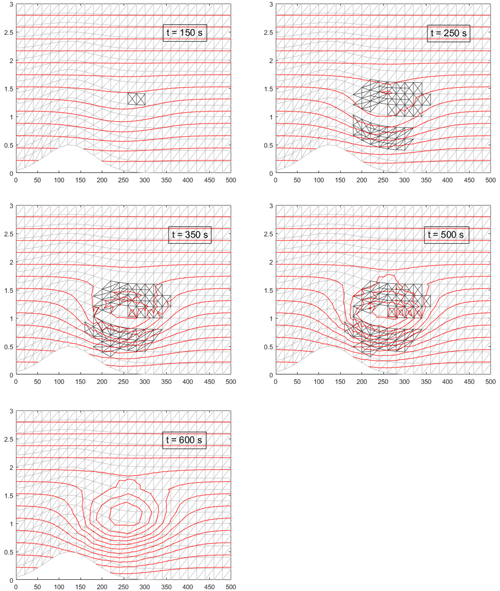
Figure 1 Snapshots of the isolines of the entropy (potential temperature) field at selected times for the numerical example described in Sect. 4 (distances along the axes are in km).

For our simulation, a standard atmosphere was chosen with an effective height H = 4.5 × 10⁴ m and surface temperature T₀₀ = 288 K (see Eq. 38; in this case β₀≈0.75). A section of the atmosphere with a total length of 500 km and height of 3 km was split initially into 25 layers in the horizontal and 15 layers in the vertical, which resulted in 750 triangles. To simulate a convective event, we added a term qλ to the Hamiltonian density in Eq. (36), so that the equation for entropy in Eq. (40) (the first equation in the second line) included an additional term equal to q in the RHS (a local heat source). We assumed that the heat source had a Gaussian shape, in both space and time, with characteristic scales of 100 km in the horizontal, 500 m in the vertical and 200 s in time. The source was centred at a height of 1 km. The maximal intensity of the heat source was chosen to be 0.6 W kg⁻¹, which corresponds to a rain rate of 1 mm h⁻¹. To simulate the effects of topography, a hill of 500 m height, stretching for 80 km in the horizontal (also of Gaussian shape) centred at 125 km, was included. Boundary conditions correspond to zero mass fluxes at the top and the bottom of the atmosphere, and the motion was assumed periodic in the horizontal direction. Our simulation lasted for 600 s, and a fourth-order Runge–Kutta method was used for integration. To check the functionality of the algorithm with respect to the splitting/recombination of the triangles, the code was forced to split them if the difference in the intensity of the heat source at the vertices exceeded a certain threshold and recombine them if the difference was less than another threshold. The time step used Δt = 0.25 s was rather small due to the fact that fast-propagating sound waves are fully accounted for (see also the comment on uniqueness of mapping after Eq. 29). It was found that mass was conserved to machine precision; conservation of energy was not checked because the numerical example included heating of the atmosphere.

The isolines of entropy (i.e. potential temperature) are plotted in a series of images as solid lines in Fig. 1 for five snapshots in time. The triangles (a bit skewed due to presence of the hill) are shown by thin lines. The split triangles are emphasized. One can see the development of convection and appearance of the irregular structure within the convective cell that is due most likely to convective instability.

5 Conclusions

The dynamical core for simulation of atmospheric motion presented in this paper can be considered to be a finite-element method combined with the least action principle. It includes features of both a Eulerian and Lagrangian description of fluid motion. The discrete set of parameters representing the atmosphere at the beginning and at the end of each time step correspond to the same set of spatial points with the associated fluid particles located at these points (i.e. a Eulerian description). The evolution within a time step, however, makes use of the Lagrangian description of fluid motion. The advantages of this approach include the following:

1. For a given set of grid points and a given forward operator (i.e. the mode of interpolation), through a minimization of action, the algorithm ensures a maximal closeness (in a broad sense) of the evolution of the discrete system to the motion of the continuum atmosphere (i.e. a dynamically optimal algorithm).

2. The grid of selected discrete points can be irregular, allowing for a variable resolution in space.

3. The spatial resolution can be adjusted locally while executing calculations.

4. The use of a set of tetrahedra as finite elements in the algorithm ensures a better (piecewise linear rather than staircase) representation of topography.

5. The algorithm automatically calculates the evolution of passive tracers by following the trajectories of the fluid particles, which ensures that all passive tracer properties required a priori are satisfied.

For demonstration purposes, the algorithm presented here considers only the very simple case of a dry atmosphere and the evolution of an arbitrary number of passive tracers. To consider a real atmosphere, one has to add heat sources and turbulent stresses to the RHS of Eq. (25). To include heating/cooling of the atmosphere, passive tracers such as water vapour and hydrometeors need to be added to the development. Their influence can be accounted for by considering the variation of entropy of the fluid particles at each time step by including heat exchange processes at the grid vertices, or, more accurately if needed, with account of the motion of the fluid particles. At this stage, one would need information regarding brightness temperatures from corresponding radiative transfer calculations. The effects of turbulence can also be included by adding Reynolds stresses τ_ij to the development through an additional term

$$\sum _{i,j}{\mathit{\tau }}_{ij}\partial {\mathit{\xi }}_i/\partial a_j$$

in action (Eq. 21) and integration over the tetrahedra, which would provide the corresponding contributions to the evolution of momenta in Eq. (25).

Future work should consider standard tests for a dynamical core and possibilities for code optimization.