the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Improvements to the use of the Trajectory-Adaptive Multilevel Sampling algorithm for the study of rare events
Daniele Castellana
Henk A. Dijkstra
The Trajectory-Adaptive Multilevel Sampling (TAMS) is a promising method to determine probabilities of noise-induced transition in multi-stable high-dimensional dynamical systems. In this paper, we focus on two improvements of the current algorithm related to (i) the choice of the target set and (ii) the formulation of the score function. In particular, we use confidence ellipsoids determined from linearised dynamics in the choice of the target set. Furthermore, we define a score function based on empirical transition paths computed at relatively high noise levels. The suggested new TAMS method is applied to two typical problems illustrating the benefits of the modifications.
- Article
(4937 KB) - Full-text XML
- BibTeX
- EndNote
Systems from various areas of physics exhibit multiple stable states. In such multi-stable systems, transitions between states can occur as a result of small-scale processes, usually referred to as noise-induced transitions (Ashwin et al., 2012). Typical elements in the Earth's system which show multistability include the Greenland Ice Sheet (Ridley et al., 2010; Robinson et al., 2012), the Amazon rainforest (Higgins and Scheiter, 2012; Lasslop et al., 2016) and the Atlantic Meridional Overturning Circulation (AMOC). In particular, the latter can undergo transitions to a collapsed state due to fluctuations in the surface freshwater forcing (Castellana et al., 2019).
A central issue in models of these multi-stable systems is the computation of transition probabilities between different states. If we exclude very special classes of systems, analytical results are generally not available. The Eyring–Kramers formula (Eyring, 1935; Kramers, 1940), which allows the computation of transition rates for reversible processes in the zero noise limit, has been recently generalised to non-gradient systems (Bouchet and Reygner, 2016). However, this method involves the calculation of quasi-potentials, which are generally hard to compute from their variational characterisation. From the numerical point of view, the naive method would be to follow a Monte Carlo approach by performing simulations of large ensembles of trajectories and calculate transition probabilities by counting the number of trajectories which actually undergo a transition. However, if the occurrence of a transition is a rare event, such computations are not feasible. For instance, to sample an event of probability , one would need to compute at least trajectories (), which is currently impossible to achieve for large-dimensional dynamical systems, where time integrations are expensive.
In order to sample tails of distributions more effectively, various methods have been developed, generally referred to as rare-event algorithms. One of the promising methods to compute transition probabilities is the Trajectory-Adaptive Multilevel Sampling (TAMS) method (Lestang et al., 2018). Its underlying idea is to perform a selection/mutation process that discards trajectories going away from a certain target set and splits/branches from those that get closer to this set. A very similar algorithm (Adaptive Multilevel Splitting or AMS), based on the same approach, has been used in the study of transitions in Jupiter's turbulent dynamics (Bouchet et al., 2019) and in molecular dynamics to compute the expected dissociation time between a protein and its ligand (Teo et al., 2016). In these studies, AMS proved to be a powerful tool that reduced computational costs by several orders of magnitude. Indeed, the required minimum number of computed trajectories scales like (Cérou et al., 2016), which is exponentially better than that for the Monte Carlo estimation. The aforementioned selection and mutation process of discarding and branching trajectories is carried out according to a score function, which allows us to rank trajectories. Rolland and Simonnet (2015) have shown that the choice of the score function plays an important role in the performance of the algorithm, even for systems with only 2 degrees of freedom. When using non-optimal score functions, especially near phase transitions, the variance of the estimated probability can peak and the convergence of the algorithm can be slow.
The aim of this work is to propose improvements to the use of the TAMS algorithm to be able to compute transitions in multi-stable systems more efficiently. The first type of improvement is the choice of the target set, which is often determined from rather arbitrary thresholds. This choice also raises more broadly the question of a precise definition of what we consider a noise-induced transition between two (stable) states. In the second type of improvement, we propose a more systematic method of defining a score function, i.e. based on empirical transition paths. The modified TAMS method is first applied to an idealised gradient system and then to a system representing a box model of the AMOC (Castellana et al., 2019).
In Sect. 2, we describe the methods developed to improve the TAMS algorithm. In Sect. 3 we show how to incorporate these techniques into the definition of the score function and present the results for idealised dynamical systems and the AMOC model. A discussion follows in Sect. 4, assessing the strengths and the limitations of the new TAMS method.
2.1 Transition probabilities using TAMS
We consider finite-dimensional dynamical systems described by stochastic differential equations (SDEs) of the following form:
where Xt∈ℝn and is the drift field. The noise term Wt∈ℝm consists of m independent Wiener processes, with the matrix being the noise matrix.
A prominent example of such a system is a model of a free particle moving in a two-dimensional double-well potential (with ). The drift term in the time-evolution equation for the variables x and y is in this case
where V(x,y) represents the potential (Fig. 1a). In the deterministic case (i.e. G=0), the stable steady states of the system are and , while the unstable steady state is . Without fluctuations, a particle starting in XA stays in XA. However, because of the presence of unresolved processes (such as thermal fluctuations), modelled by the noise term in the SDE, the particle can move away from XA and in some cases make the transition to the state XB. An example of such a transition is shown in Fig. 1b.
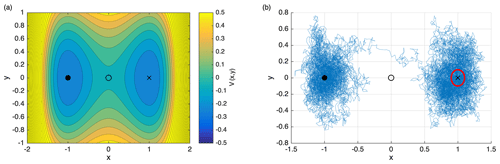
Figure 1(a) Iso-potential contours corresponding to the double-well potential (Eq. 2). The two stable steady states and are marked with a filled circle and a cross, respectively. The saddle is indicated by a circle. (b) Example of a noise-induced transition from XA to XB for a particle moving in the double-well potential in (a). The noise matrix in the general SDE (1) is chosen as G=σI, with σ=0.32. The red circle denotes an arbitrarily defined target set B.
The transition probability that a trajectory starting in XA reaches a neighbourhood B around XB before time T is indicated by . Here, τB denotes the stopping time associated with reaching B. The TAMS algorithm is based on a selection and mutation process of discarding and branching trajectories, which are ranked according to a score function . For a given state , ϕ(X,t) is supposed to measure how likely it is to start in (X,t) and reach B before time T. As a consequence, if the choice of score function is successful, the probability that a trajectory reaches the target set B keeps increasing at each iteration of the algorithm, which is why this method is more efficient than brute-force techniques. A visual representation of the algorithm is given in Fig. 2 and a step-by-step description is provided in Appendix A (more details can be found in Lestang et al., 2018).
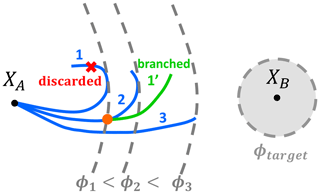
Figure 2Illustration of the TAMS algorithm. First, simulate N trajectories starting in XA (N=3 blue trajectories in the figure). The trajectories are ranked according to their score ϕi, which is the maximum value of the score function ϕ along the trajectory. Then, at each iteration, the trajectory with the lowest score (1 in the figure, with score ϕ1) is discarded. It is replaced by picking a trajectory uniformly at random from the other ones (2 in the figure), then computing the earliest position at which it reaches a higher score than the discarded trajectory (orange dot) and finally using this position as the branching point for the new trajectory (1′). This is repeated until all the trajectories reach B or the number of iterations reaches a predefined limit.
2.2 Score functions
Consider a general SDE (1) and two stable states XA and XB of the corresponding deterministic system. The TAMS algorithm (see Appendix A) needs a score function to be defined, which allows us to rank trajectories and select the ones to discard. The optimal score function ϕcom(X,t), i.e. the score function that minimises the variance of the probability estimator, is called the static committor. Its generic expression is given by the following conditional probability (Lestang et al., 2018):
where T is again the fixed duration of the trajectories and τB is the stopping time associated with reaching the target set B. In other words, ϕcom(X,t) is the probability that a trajectory starting in X at time t reaches B before time T. This expression is quite natural because ideally, the score of (Y,s) should be higher than the score of (X,t), i.e. , if and only if . This condition is clearly satisfied by ϕcom (and in fact any increasing function of ϕcom). However, the expression given in Eq. (3) is generally unusable because it is the very quantity that we want to compute. For instance, ϕcom(XA,0) is precisely the transition probability that TAMS estimates. As a conditional probability of the form , the committor ϕcom(X,t) satisfies the backward Fokker–Planck equation (Lestang et al., 2018):
However, solving the backward Fokker–Planck equation in systems with many degrees of freedom is computationally unfeasible. Moreover, even if the committor is available on a grid used for the discretisation of Eq. (4), using interpolation to evaluate it during a TAMS loop can also have a prohibitive computational cost.
Bouchet et al. (2019) made use of a score function based on the distances of the state X from the starting state XA and the destination equilibrium XB, respectively. It is defined as
Alternatively, a Gaussian-shaped score function ϕgauss was proposed in Baars (2019). It is defined as
with . Here β∈ℝ is a parameter controlling the decay and XC is the saddle state of the system. Due to the general expressions of ϕgauss and ϕdist, these score functions can be used in systems of any dimension.
2.3 Definition of the target set
Once the score function has been chosen, a threshold needs to be defined for the TAMS algorithm to converge, so that the occurrence of a transition can be detected. In other words, we do not expect each trajectory that undergoes a transition to reach exactly the destination equilibrium XB, but rather a neighbourhood of it (B). The target set B can then be defined according to a level set ϕtarget of the score function ϕ:
However, different score functions ϕ and different level sets ϕtarget correspond to different target sets B, which can differ in volume and in shape. Moreover, often the level set ϕtarget is defined somewhat arbitrarily. For example, by using ϕgauss with target score or 0.95, we found that the average of the transition probability estimator for a two-dimensional double-well potential system (Eq. 2) can vary by up to 30 %. This may not be a concern if one only cares about the order of magnitude of the transition probability, but it will be problematic if quantitative comparisons are needed. Moreover, a poor choice of target set can lead to inaccuracies when a trajectory has a score greater than ϕtarget without actually making the transition in all the degrees of freedom. Thus, there is a need to define a canonical choice of a target set B, which needs to fundamentally address what is considered to be a noise-induced transition.
For this purpose, we use the concept of a confidence ellipsoid. This is an ellipsoidal neighbourhood around a stable equilibrium state, inside which a trajectory subject to the locally linearised dynamics stays, within a certain confidence level (Cowan, 1998).
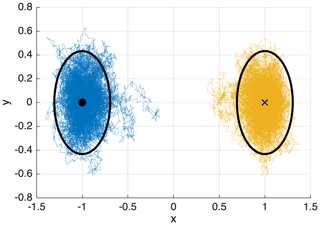
Figure 3Confidence ellipsoids for the two-dimensional double-well potential system (Eq. 2), with confidence level and noise matrix G=0.25I, where I is the identity matrix in ℝ2. Two trajectories of duration T=200 are shown: one (blue) is initialised at the initial state and one (orange) at the target state. 93 % of the points composing a trajectory are inside their corresponding ellipsoid. This is lower than the prescribed confidence level because away from the equilibrium, the first-order dynamics from which the confidence ellipsoids are derived does not hold.
Consider a general SDE system given by Eq. (1). Because the drift vanishes at an equilibrium state F(XB)=0, its first-order approximation around the equilibrium state XB via Taylor expansion is
where is the Jacobian matrix of F at XB. Using a translation , the first-order approximation of the SDE is then
Because the drift term has been linearised, this is the equation for an n-dimensional Ornstein–Uhlenbeck process. The stationary probability density function (PDF) f of the approximating process is Gaussian (Cowan, 1998) and given by
where is the covariance matrix of the system calculated in XB and the norm induced by its inverse , defined by . The covariance matrix CB can be thought of heuristically as the matrix containing the correlations 𝔼(xixj) (with ), which generalises the notion of variance in n dimensions. CB is obtained by solving the Lyapunov equation (see Kuehn, 2012, for the full derivation):
We then define the confidence ellipsoid, which has as a shape matrix, as follows:
where Qα is the quantile of confidence level 1−α of the n-dimensional χ2 distribution (Cowan, 1998), usually . The directions of symmetry of the ellipsoids are given by the eigenvectors of the covariance matrix CB and the radii are given by the corresponding eigenvalues and the confidence level 1−α. Intuitively, the greater the eigenvalue, the more a trajectory fluctuates in the given direction.
The (1−α)-covariance ellipsoid represents the n-dimensional volume where a trajectory is confined with confidence level 1−α, provided its dynamics is well approximated by the first-order expansion at the equilibrium point. An illustration of the 0.95-confidence ellipsoid for the double-well potential is shown in Fig. 3. The confidence ellipsoid ℰ constitutes a way to meaningfully define the target set B with minimal arbitrary parameters. As shown in Fig. 3, when initialising a trajectory at XA or XB in the two-dimensional double-well system, it stays inside the correspondent ellipsoid with a certain confidence . In the next section, we show how to incorporate this choice of target set into the score function ϕ.
2.4 Estimating the typical transition path using histograms
The second line of improvement of the score function concerns the estimation of typical transition paths of the dynamical system. In the zero noise limit, the Freidlin–Wentzell theory of large deviations predicts that transition paths will cluster around the most probable transition path, called the instanton (Freidlin and Wentzell, 1984). On the other hand, in the finite noise regime, transition paths may deviate from the instanton. Moreover, instantons may be computationally inaccessible for systems with many degrees of freedom. Therefore, it can prove more relevant to estimate empirically the typical transition path that the system follows at a given finite noise level, which is the approach we follow here.
The idea is to first accumulate transition paths at a noise level where transitions are frequent enough (typically ) so that any sampling method (direct Monte Carlo or TAMS with naive score functions) can be used. Then, we compute the spatial histogram of the transition paths over a discretised phase space using n-dimensional boxes. This provides the spatial distribution of the transition paths, which is concentrated around a typical transition path, reminiscent of an instanton phenomenology, which was also observed in more complex systems (Bouchet et al., 2019). From the spatial histogram, we extract a typical transition path.
The main steps of the path-finding algorithm are listed below:
- i.
the trajectory of the typical transition path starts in the box of the histogram containing the initial state XA;
- ii.
the next box in this trajectory corresponds to the neighbour which has the highest nonzero histogram value but which has not already been visited by the typical transition path;
- iii.
the algorithm stops if it reaches the box containing the target state XB.
In addition, the full typical path estimation algorithm uses a self-correcting method to avoid dead ends when there are no valid neighbours to be the next point in the trajectory. The spirit of the path-finding algorithm is similar to the depth-first search algorithm (Cormen et al., 2009). We found that, as long as the histogram is not fragmented, i.e. there is a sufficient number of accumulated trajectories or large enough histogram bins, the algorithm converges. Possible artefacts created by this estimation include spiralling near the initial equilibrium (because of the concentric shell structure of the local probability density function, Eq. 10) and zigzagging at the histogram box size. They can both be addressed by a clean-up algorithm: starting from the first box, at each box Xj, if the trajectory goes back to one of its neighbours at a later time, with Xj+k being the latest neighbour visit, we erase the points from the trajectory.
In a general system, transitions induced at high noise do not necessarily follow similar transition paths at lower noise levels. However, high-noise estimates are robust as long as there is no drastic change in the behaviour of the system at an intermediate noise level, which would signal a physical phase transition in the system (Rolland and Simonnet, 2015). Moreover, we can check a posteriori if such a transition occurs by starting at high noise, gradually decrease the noise level and apply the empirical estimation of the typical path or simply compare histograms each time the noise level is decreased.
In this section, we apply both modifications to TAMS (ellipsoids in the score function and typical path estimation) to different problems.
3.1 Incorporating ellipsoids in the score function
First, we apply the modified TAMS method to the two-dimensional double-well system defined by Fig. 1. As outlined in Sect. 2.3, given any score function ϕ, we want the target set to coincide with the 0.95-confidence ellipsoid ℰ associated with the equilibrium state XB. However, because the contour levels of ϕ, in general, do not have the shape of an ellipsoid, there is no suitable choice of ϕtarget such that B coincides with ℰ. Here, we propose a general method to modify any score function ϕ so that we are able to choose the target set B to be exactly the 0.95-confidence ellipsoid ℰ of XB.
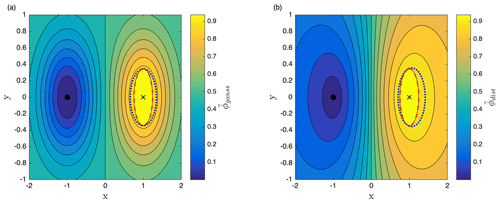
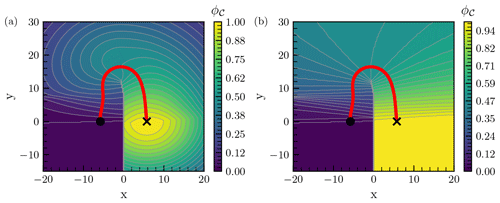
Figure 4(a) Contour levels of the modified score function , for the two-dimensional double-well system represented in Fig. 1, according to the procedure described in Eq. (14). The level set ϕtarget (dotted blue line) of the former score function ϕgauss is tangent to the ellipsoid. The level set (dotted red) of the modified score function coincides with the ellipsoid. (b) Same plot for the score function .
We first compute the level , defined as the minimum of the score function ϕ on the confidence ellipsoid ℰ:
such that the set contains the ellipsoid ℰ and is tangent to ℰ. This can be done numerically by generating a mesh of points around XB, then selecting the points inside ℰ by comparing their norm with the quantile Qα and finally computing the minimum of ϕ on these points. Then, define the modified score function in the following way:
The target set for the modified score function turns out to coincide with ℰ. We apply this procedure on both the score functions ϕgauss and ϕdist, and the results for the improved score functions and are shown in Fig. 4.
3.2 Designing a score function based on a typical transition path
In order to show how to design a score function based on a typical transition path, we consider a two-dimensional system slightly less trivial than the double-well system, i.e. a two-dimensional system with the following potential,
depicted in Fig. 5a. It consists of two energy minima at and and a potential barrier spanning y<15 and at x=0. The dynamics is then given by the SDE (1), with drift .
The dynamics of the system is quite interesting, as it exhibits two distinct regimes for transition paths, depending on the noise level σ (assuming G=σI). At high noise (σ2≫ΔV, where the potential barrier height is ), trajectories are likely to cross the potential barrier. At low noise (σ2≪ΔV), trajectories are not likely to cross the barrier, and the trajectories which undergo the transition instead go through the upper channel at y≈15. Typical examples of such trajectories are shown in Fig. 5b. Rolland and Simonnet (2015) investigated the convergence properties of AMS using a triple-well potential system, which also exhibits two regimes of preferred transition paths depending on the noise. They found a strong dependency of the statistics of the rare-event algorithm (e.g. the number of iterations) and the duration of reactive trajectories on the choice of score function. We expect the same behaviour when applying TAMS to the system with potential (Eq. 15) and that this system will reveal differences in performance between various score functions.
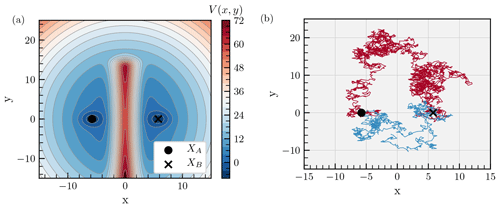
Figure 5(a) Potential landscape of the two-dimensional gradient system defined by Eq. (15). Two energy minima are located at and . They are separated by a potential barrier spanning y<15 and at x=0. (b) Typical transition paths from XA to XB for two noise levels σ. At high noise, trajectories can cross the potential barrier (σ=10, blue). At low noise, trajectories go through the upper channel (σ=3, red).
Figure 6a shows a histogram computed with 300 transition paths for the system with the potential given by Eq. (15), with noise level set at σ=3. We need enough trajectories so that the histogram gives an accurate representation of all possible transition paths and that fluctuations along the typical path can be effectively averaged out by the path estimation algorithm. One way to verify that there are enough trajectories is to check that the histogram near the equilibria is similar to the Gaussian stationary distribution that arises from locally linearised Ornstein–Uhlenbeck dynamics. For example, starting from an equilibrium point and picking any direction, then if for the first few histogram cells the histogram value is not decreasing (as would be the case for a Gaussian distribution), this would mean that too few trajectories were used. The typical transition path was estimated using the algorithm sketched in Sect. 2.4. As already mentioned, some artefacts created by the estimation (such as spiraling or zigzagging) can be corrected using a clean-up algorithm. The result is shown in Fig. 6b: the empirical estimation of the typical path resembles the instanton around which the transition paths are clustered at lower noise (Fig. 6b, blue path). The instanton was calculated by implementing the geometric minimum action method (Heymann and Vanden-Eijnden, 2008). Note that if, instead, we accumulated trajectories at high noise σ>10, we would obtain trajectories going from XA to XB in a straight line, which is the typical path at high noise similar to Rolland and Simonnet (2015). This typical transition path is then substantially different from the instanton, which goes through the upper channel. Thus, our method can be advantageous in multistable systems where the typical transition path depends on the noise level. We can start at high noise and reapply the empirical estimation of the typical path each time the noise level is decreased.
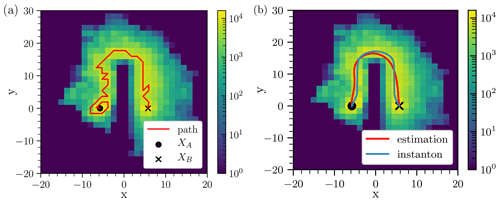
Figure 6(a) Histogram of N=300 transition paths at noise level σ=3, using the modified score function with β=1.5, defined by Eq. (6) and implemented with Eq. (14). The corresponding transition probability () is high enough so that direct Monte Carlo sampling could have been used to produce a similar histogram. The bin resolution (Δx=1.4, Δy=1.75) is coarse for illustration purposes. The histogram is used as input in the path-finding algorithm which produces the transition path in red. Grid-scale spiralling occurs near the initial state XA because of the concentric shell structure of the local probability density function given by Eq. (10). (b) Same histogram as panel (a). The estimated typical transition path (red) has been cleaned up from its grid-scale spiraling and zigzags with the clean-up algorithm and has then been smoothed. It strongly resembles the instanton (blue) which was computed by implementing the geometric action minimum method (Heymann and Vanden-Eijnden, 2008).
Given a typical transition path 𝒞, we present the design of a score function ϕ𝒞 which encourages trajectories to follow the transition path 𝒞 such that it gives a reasonable approximation of the static committor. Let us consider a trajectory 𝒞(s) in ℝn parameterised by arclength . Then we define the score function ϕ𝒞, called the path-based score function, such that it grows from 0 to 1 along the trajectory from XA to XB and decays exponentially along the direction transverse to the trajectory:
where is the distance between X and the trajectory 𝒞(s), s(X,𝒞) is the curvilinear coordinate of the position on the trajectory that satisfies the infimum in the definition of d(X,𝒞) and d0 is the characteristic decay length (free parameter). The score function ϕ𝒞 is shown in Fig. 7 for the estimated transition path 𝒞 shown in Fig. 6 and two values of decay length d0=20 and d0=200.
The score function increases from 0 to 1 along the trajectory. Thus, it encodes the preferred direction that the system has to follow. This contrasts with the generic score functions ϕgauss and ϕdist, which are symmetrical in y: they do not contain the information that the system has to increase in y in order to make the transition to XB. Note that the method we developed here can be applied, in principle, to systems of any dimension. As shown in Fig. 7b, the score function ϕ𝒞 is discontinuous because the trajectory has positive curvature. The discontinuity is located near the axis x=0. Indeed, when crossing the axis x=0, the closest point on 𝒞 changes and s(X,𝒞) is discontinuous.
Next, we applied TAMS with the path-based score function ϕ𝒞 to the two-dimensional system in Eq. (15). We compare its performance with the previously defined score functions ϕdist and ϕgauss. In fact, we use the associated modified score functions, such that the target set B matches the 0.95-confidence ellipsoid (we drop the tildes for readability). We use the following parameters: duration of a trajectory T=20, time step dt=0.01, and N=100 trajectories in the ensemble, which we found was enough to ensure that the interquartile range of the independent realisations spans less than 1 order of magnitude around the mean for most noise levels.
We show in Fig. 8a the transition probability estimates using the score functions ϕdist, ϕgauss (with β=1.5) and ϕ𝒞 (with decay parameters ) averaged over 10 instances of the algorithm. The probability estimates are in good agreement with each other and with a Monte Carlo estimation for σ>2.5. The score function ϕ𝒞 is robust with respect to the choice of the decay length d0.
The performances of the numerical methods are next measured using the work-normalised relative error ϵ, which combines the variance of the algorithm and its computational cost (Glynn et al., 2009):
where and are the mean and standard deviation of the probability estimate over the different instances, and ω is the average number of time steps calculated in one realisation. In short, ϵ measures how precise the numerical method is at equal computational cost. The smaller the ϵ, the better the algorithm performs.
The results are shown in Fig. 8b. For the system in Eq. (15), the score functions ϕdist, ϕgauss and ϕ𝒞 have little difference in performance. For the lowest noise values, the path-based score function has at most a 30 % smaller error ϵ than the score function ϕgauss. Changing the decay length d0 hardly changes the error ϵ. When adjusting the parameters of the potential V or applying the same method to the triple-well system used in Rolland and Simonnet (2015), the performance gain, while often present, never systematically exceeded 30 %. All in all, in this category of two-dimensional systems, using the path-based score function approach yields little improvement.
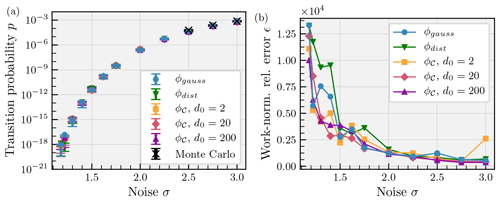
Figure 8(a) Transition probability p as a function of noise parameter σ. Mean estimates and interquartile range (error bars) over Nsamples=10 independent realisations of the TAMS algorithm using the score functions ϕdist (green down triangle), ϕgauss (with β=1.5, blue circle) and ϕ𝒞 with decay parameters (yellow square, pink diamond, purple up triangle) are shown. The Monte Carlo estimate (black cross) has been run with trajectories with the target sets coinciding with the confidence ellipsoids around XB, with associated standard deviation (error bars). There is an overall good agreement between the numerical estimations. The path-based score function is robust to the choice of decay parameter. (b) Performance of the score functions measured by the work-normalised error ϵ as a function of noise σ (same markers as panel a). At most, there is a 30 % decrease in error when using the path-based score function ϕ𝒞 at low noise. Note that at high noise σ=3, using a short decay length d0=2 with ϕ𝒞 leads to poor performance because the greater values of ϕ𝒞 are tightly concentrated around the estimated instanton, whereas typical transition paths are not necessarily clustered around it. Otherwise, the performances of the score functions are roughly similar.
3.3 Transition probabilities in a box model of the AMOC
Finally, as a main application of the modification of the target set B into a confidence ellipsoid ℰ, we consider the dynamical system in Castellana et al. (2019), which represents a box model of the AMOC. The system consists of a set of stochastic differential equations, plus one algebraic constraint, the latter representing the salt conservation in the model (as shown in Appendix B). This model can be formulated as
In the equations above, we split the state of the system Xt into two parts: Yt, which includes salinities of four of the boxes plus the depth of the pycnocline D, and Zt, which represents the salinity of the deep box (Sd). As the noise is applied only to the asymmetric component of the atmospheric freshwater flux (Ea), it directly affects only two of the variables: Sn and Ss. Moreover, the stochastic increments associated with the two variables are identical to make sure that each decrease in freshwater forcing in the southern box results in the same increase in it in the northern box in the model. Therefore, the noise is not spatially independent, and the noise matrix G is no longer diagonal: it consists of a (5×1) row vector, with only two elements different from zero. For a reasonable choice of the parameters, the deterministic system is in a bistable regime (Castellana et al., 2019), which means that there are two possible equilibrium states under the same forcing conditions. In general, we are interested in studying transitions between the present-day AMOC (XA) and the collapsed state (XB).
For a differential-algebraic system of equations (DAEs), such as the system in Eq. (18), we need to be particularly careful while computing the covariance ellipsoids. First of all, we make use of the Schur complement of the Jacobian of the system, which allows us to calculate the covariance matrix when an algebraic constraint is present (Baars et al., 2017). Nevertheless, the resulting matrix CB is singular, with two eigenvalues being equal to zero. One of the corresponding eigenvectors is a vector pointing in the direction of the variable D (depth of the pycnocline). The reason behind it is that the differential equation governing the evolution of D does not contain any of the other variables (see Castellana et al., 2019) when the system is in the collapsed state (XB). This results in D not being affected by the noise, as this is imposed only on two of the salinities. Hence, we compute the covariance matrix relative to the salinities, removing 1 degree of freedom from the original matrix. Unfortunately, such a matrix still has one zero eigenvalue, which is due to the salinity conservation (the algebraic equation in the system Eq. 18). To overcome this problem, we compute the Moore–Penrose inverse (or pseudo-inverse) of the covariance matrix, , by performing a singular value decomposition of and removing the zero eigenvalue, together with the corresponding eigenvector (Ben-Israel and Greville, 2003). A two-dimensional projection of the ellipsoid constructed for the box model is shown in Fig. 9.
For the system in Eq. (18), the modified score function is more complicated, as the covariance matrix used to construct the ellipsoid contains only the degrees of freedom related to the salinities of the model, leaving the variable D (depth of the pycnocline) out. From a geometric point of view, that means that the covariance ellipsoid around XB is degenerated along the D direction. Figure 9 shows a projection of the ellipsoid – once the noise amplitude is fixed – onto the plane identified by the variables Sn and Ss (respectively, the salinity of the northern box and the one of the southern box in the model). The projection was obtained by calculating the conditional covariance matrix of the two variables under consideration, given that the other variables are set on their mean value (Wasserman, 2013). The two-dimensional ellipse contains the large majority of the projected time points (on the same plane) of a trajectory that wanders around the equilibrium. By construction, the confidence level of the confinement is higher than the one prescribed for the full-dimensional ellipsoid (in this case 0.95). Clearly the level sets of the score function ϕgauss do not coincide with the one of the ellipsoid. Hence, the importance of modifying the score function appears evident.
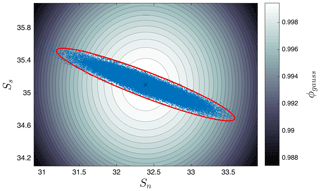
Figure 9Level sets of the score function ϕgauss in proximity to the collapsed equilibrium state XB of the system in Castellana et al. (2019), projected onto the plane identified by the variables Sn and Ss (respectively, the salinity of the northern box and the one of the southern box in the model). A trajectory of the system, initiated in the collapsed state, has been projected onto the same plane (blue circles). The red ellipse is the two-dimensional projection of the covariance ellipsoid constructed by using the matrix and a confidence level of 0.95; 98 % of the points comprising the trajectory are inside the ellipsoid.
When constructing an improved score function, in order to evaluate whether a state belongs to the neighbourhood of XB, we need to check two conditions: (i) whether the state of the system is inside the salinity covariance ellipsoid drawn around the destination equilibrium and (ii) whether the variable D of the state is the same as the one of XB. Hence, the improved score function for the box model reads as
where XS indicates the part of the state vector representing the set of the salinities, whereas XD represents the variable D. As already mentioned, to check whether a certain state belongs to the salinity ellipsoid, we made use of the pseudo-inverse of in the definition of Eq. (12).
To be able to assess the relevance of a proper definition of the target set in the TAMS algorithm and hence the importance of using the improved version of the score function, we computed transition probabilities of the AMOC from the present-climate state to the collapsed state for reasonable values of the atmospheric forcing and noise. In particular, we chose and fσ=0.16. This last value represents the ratio between the standard deviation of the noise in the atmospheric forcing and its mean value (Castellana et al., 2019). The number of trajectories used in the algorithm was set to 100, and the timescales at which the probabilities were evaluated were chosen to be 1000 and 10 000 years, respectively. For each transition probability, we used three different versions of the algorithm, based on three different settings for the score function. The first two versions were implemented by using ϕgauss in Eq. (6), with two different choices for the threshold ϕtarget. In the third version, we used as defined in Eq. (19), where the starting score function was ϕgauss. Each probability was calculated by running 15 instances of the algorithm and then computing the median and the interquartile range (IQR). The results are shown in Table 1 below.
When running TAMS to compute transition probabilities between two states of the Atlantic circulation in this model, with different versions of the score function, we found a considerable discrepancy between the obtained values. In particular, it appears that setting a very high threshold in the Gaussian score function makes the algorithm detect no transitions (we set up the algorithm so that it stops when the probabilities involved are smaller than 10−9): the reason behind this is that, because of the presence of the noise, we do not expect the state of the system to stay indefinitely close to the destination equilibrium but rather to wander around it. Therefore, the score function, which assigns the maximum score only to a very small neighbourhood of the equilibrium, is not able to properly recognise transitions. Moreover, it is not surprising that, when using ϕgauss with a smaller value of ϕtarget (0.99) or , we obtain different results: as the shape of the covariance ellipsoid is not spherical (see Fig. 9), we expect ϕgauss to detect transitions even though the state is actually still far from the destination equilibrium, at least in certain directions. As a general rule, we expect ϕgauss to give results different from ϕbox as long as the ellipsoid of the system is not spherical, regardless of the choice of the threshold ϕtarget.
We presented and applied several improvements to the TAMS rare-event algorithm, when used to compute transitions in multistable systems. The first improvement was based on a more rigorous criterion to define noise-induced transitions involving confidence ellipsoids ℰ to formalise this criterion. In turn, this led to the rigorous choice of the target set B=ℰB, which was traditionally set by rather arbitrary thresholds. We then showed how to incorporate this definition of B into the score function . For certain classes of systems, like the ones containing algebraic constraints in addition to differential equations or when the noise does not affect one or more directions in the variable space (i.e. the associated covariance matrix is singular), this method requires some precautions. In particular, for the box model in Castellana et al. (2019), we had to adapt the definition of the improved score function in Eq. (19) as well as calculate the pseudo-inverse matrix of the covariance matrix in order to compute the ellipsoid.
This method, while quite general, has several limitations. While the modified score function is continuous outside B, it is constant in the domain (see Fig. 4). This means that in the TAMS algorithm, branching will never occur inside M, but at the boundary ∂M. This can have an influence on the convergence of TAMS if the level sets of the initial score function ϕ have a pathological shape near XB and the spatial extension of D is not negligible. Nevertheless, we expect this to have little impact because this phenomenon is localised near the target state XB. Therefore, the trajectories will naturally converge towards XB as a result of the dynamics, even without the help of the branching process of TAMS. However, to ensure that the confidence ellipsoid ℰ defines a meaningful target set, one needs to be sure that ℰ is contained inside the basin of attraction of the target state XB. While this is the case in the limit of small noise σ→0, it might not be the case for finite noise. A solution to this issue would be to compute the basin of attraction 𝒱 of XB and define the target set B as the intersection . However, we expect that, in the generic case, this occurs when the noise level σ is high enough so that transitions are less rare and that a direct Monte Carlo estimation is sufficient to estimate transition probabilities.
Next, we proposed a systematic method of defining a score function, designed to approximate the static committor, based on empirical transition paths. We proposed an algorithm to estimate the typical transition path under a high noise level, which is then used to define a family of score functions with a single decay parameter d0. We applied our method to a two-dimensional well with a potential barrier. We found that our typical path estimation gave satisfactory results and that the associated score function ϕ𝒞, while discontinuous, remained unbiased and relatively insensitive to the change in the decay parameter d0. While we did not find significant performance improvements over existing non-trivial score functions, we think that differences will become apparent if applied to higher-dimensional systems, where there are more directions to fluctuate in. We did not show any results of the application of this method to the box model of the AMOC (Castellana et al., 2019), because for this rather complicated case, we were not able to efficiently compute typical transition paths from the trajectory histograms of the system.
One key limitation of our approach of constructing the path-based score function ϕ𝒞 is the computer memory needed to store the trajectory histogram, which becomes prohibitively huge for high-dimensional systems such as discretised partial differential equation (PDE) systems. As an example, a 50×50 two-dimensional grid storing four variables in each cell (e.g. two velocity components, pressure and a tracer) with 10 bins of resolution in each degree of freedom would require more than 10 PB of memory, which is unfeasible. However, this limitation can be easily bypassed by defining the objects needed to run the TAMS algorithm, namely the score function ϕ and the target set B, in a reduced space of much fewer dimensions. For instance, Bouchet et al. (2019) studied the dynamics of the barotropic beta-plane quasi-geostrophic equations describing Jupiter's turbulent atmosphere. While the PDE system was evolved in the full phase space, their rare-event algorithm was run in a reduced three-dimensional phase space defined by three Fourier coefficients. The target set B and the score function were defined on this reduced space. Moreover, they accumulated transition trajectories in a three-dimensional histogram and showed their concentration around instantons. By applying the path-finding algorithm, an empirical estimation of the instanton can be made. This offers a viable alternative to solving a minimisation problem in the full space to compute the instanton and then project it in the reduced space, which is next to intractable for this system.
Another way to define the reduced space 𝒱 in which to run TAMS is to consider the principal components, also called empirical orthogonal functions (EOFs), which are the eigenvectors of the covariance matrix. One idea, suggested by Baars (2019), is to retain the EOFs with the largest variance (i.e. the eigenvalue of the covariance matrix) at the initial state XA and target state XB. EOFs represent the directions in which the system fluctuates the most. They are then assumed to be the directions which capture best the noise-driven dynamics. When studying transitions in a PDE model of the Atlantic Meridional Overturning Circulation, den Toom et al. (2011) and Baars et al. (2021) projected the dynamics in a reduced space of a dimension (≈500) still too large to apply the histogram method directly. However, one idea is that the TAMS algorithm could be run in an even smaller space – (of dimension<10) – while still computing the dynamics in the space 𝒲. Then, the memory required to store a histogram becomes reasonable and our histogram method can be applied.
Another potential issue of our modified TAMS method is the fact that the score function ϕ𝒞 is discontinuous because the trajectory has positive curvature, as shown in Fig. 7b, blue path. The discontinuity is located near the axis x=0. Indeed, when crossing the axis x=0, the closest point on 𝒞 changes and s(X,𝒞) is discontinuous. In fact, in the mathematical proofs about the statistical and convergence properties of the probability estimator (Cérou et al., 2016), the score functions are assumed to be continuous. Nevertheless, in our applications, we did not detect any statistically significant bias in the probability estimator due to the discontinuity. Moreover, some meaning can be attributed to the discontinuity: it is located at the boundary between the attraction basins of XA and XB, and it thus reflects a qualitative change in behaviour in the system. Crossing this boundary means that the trajectory converges to XB instead of XA if σ=0. In addition, the remnant of a discontinuity is observed in the static committor of the similar triple-well system used in Rolland and Simonnet (2015). Indeed, their Fig. 4c shows the contour plots of the static committor in the low-noise regime. A steep gradient is present at the x=0 boundary, which gives further evidence that the discontinuity of ϕ𝒞 may not be problematic.
Further testing of the ideas presented in this work in high-dimensional systems such as discretised PDEs would give more insight as to the effectiveness of our approach compared to the more generic score functions used up to now. Moreover, incorporating some form of time dependence into the score function ϕ to specifically optimise TAMS would constitute an interesting project.

The equations determining the evolution of the AMOC in this model are the salinity budgets of the different boxes, together with the variation of the volume of the pycnocline, and the salt and volume conservation equations (Castellana et al., 2019):
where the function θ(x) is the Heaviside step function. The transports depend on the variables via the following relations:
where the density of the generic box i is defined as
The volumes depend, in turn, on the variable D:
The reference parameter values are shown in Table B1.
Table B1Reference parameters used in Eqs. (B1)–(B4) from Castellana et al. (2019).

The software is available at https://doi.org/10.6084/m9.figshare.13914353.v2 (Wang, 2021a) and https://doi.org/10.6084/m9.figshare.13919642.v1 (Wang, 2021b).
Datasets for Figs. 6 and 8 are available from Wang and Castellana (2021, https://doi.org/10.6084/m9.figshare.13918100.v1).
PW and DC designed the algorithms, ran the simulations and prepared the figures. All the authors discussed the results and contributed to the writing of the manuscript.
The authors declare that they have no conflict of interest.
The authors thank Sven Baars for insightful discussions. Pascal Wang acknowledges the hospitality of the Institute for Marine and Atmospheric research Utrecht where the scientific work was conducted.
This research has been supported by the European Commission, H2020 Research Infrastructures (CRITICS (grant no. 643073)).
This paper was edited by Balasubramanya Nadiga and reviewed by two anonymous referees.
Ashwin, P., Wieczorek, S., Vitolo, R., and Cox, P.: Tipping points in open systems: bifurcation, noise-induced and rate-dependent examples in the climate system, Philos. Trans. Royal Soc. A, 370, 1166–1184, https://doi.org/10.1098/rsta.2011.0306, 2012. a
Baars, S.: Numerical methods for studying transition probabilities in stochastic ocean-climate models, PhD thesis, Rijksuniversiteit Groningen, Groningen, 2019. a, b
Baars, S., Viebahn, J., Mulder, T., Kuehn, C., Wubs, F., and Dijkstra, H.: Continuation of Probability Density Functions Using a Generalized Lyapunov Approach, J. Comput. Phys., 336, 627–643, https://doi.org/10.1016/j.jcp.2017.02.021, 2017. a
Baars, S., Castellana, D., Wubs, F. W., and Dijkstra, H. A.: Application of adaptive multilevel splitting to high-dimensional dynamical systems, J. Comput. Phys., 424, 109876, https://doi.org/10.1016/j.jcp.2020.109876, 2021. a
Ben-Israel, A. and Greville, T. N.: Generalized inverses: theory and applications, vol. 15, Springer Science & Business Media, Springer-Verlag New York, 2003. a
Bouchet, F. and Reygner, J.: Generalisation of the Eyring–Kramers Transition Rate Formula to Irreversible Diffusion Processes, Ann. Henri Poincare, 17, 3499–3532, https://doi.org/10.1007/s00023-016-0507-4, 2016. a
Bouchet, F., Rolland, J., and Simonnet, E.: Rare Event Algorithm Links Transitions in Turbulent Flows with Activated Nucleations, Phys. Rev. Lett., 122, 074502, https://doi.org/10.1103/PhysRevLett.122.074502, 2019. a, b, c, d
Castellana, D., Baars, S., Wubs, F. W., and Dijkstra, H. A.: Transition probabilities of noise-induced transitions of the Atlantic ocean circulation, Sci. Rep., 9, 1–7, https://doi.org/10.1038/s41598-019-56435-6, 2019. a, b, c, d, e, f, g, h, i, j, k
Cérou, F. and Guyader, A.: Fluctuation analysis of adaptive multilevel splitting, Ann. Appl. Prob., 26, 3319–3380, https://doi.org/10.1214/16-AAP1177, 2016. a, b
Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C., eds.: Introduction to algorithms, MIT Press, Cambridge, Mass., 3rd edn., oCLC: 698955316, 2009. a
Cowan, G.: Statistical data analysis, Oxford university press, USA, 1998. a, b, c
den Toom, M., Dijkstra, H. A., and Wubs, F. W.: Spurious Multiple Equilibria Introduced By Convective Adjustment, Ocean Model., 38, 126–137, https://doi.org/10.1016/j.ocemod.2011.02.009, 2011. a
Eyring, H.: The Activated Complex in Chemical Reactions, J. Chem. Phys., 3, 107–115, https://doi.org/10.1063/1.1749604, 1935. a
Freidlin, M. I. and Wentzell, A. D.: Random Perturbations, Springer, New York, NY, 15–43, https://doi.org/10.1007/978-1-4684-0176-9_2, 1984. a
Glynn, P., Rubino, G., and Tuffin, B.: Robustness properties and confidence interval reliability issues, in: Rare Event Simulation using Monte Carlo Methods, John Wiley & Sons, New Jersey, USA, 63–84, https://doi.org/10.1002/9780470745403.ch4, 2009. a
Heymann, M. and Vanden-Eijnden, E.: The geometric minimum action method: A least action principle on the space of curves, Commun. Pure Appl. Math., 61, 1052–1117, https://doi.org/10.1002/cpa.20238, 2008. a, b
Higgins, S. I. and Scheiter, S.: Atmospheric CO2 forces abrupt vegetation shifts locally, but not globally, Nature, 488, 209–212, https://doi.org/10.1038/nature11238, 2012. a
Kramers, H.: Brownian Motion in a Field of Force and the Diffusion Model of Chemical Reactions, Physica, 7, 284–304, https://doi.org/10.1016/s0031-8914(40)90098-2, 1940. a
Kuehn, C.: Deterministic Continuation of Stochastic Metastable Equilibria via Lyapunov Equations and Ellipsoids, SIAM J. Sci. Comput., 34, A1635–A1658, https://doi.org/10.1137/110839874, 2012. a
Lasslop, G., Brovkin, V., Reick, C. H., Bathiany, S., and Kloster, S.: Multiple stable states of tree cover in a global land surface model due to a fire-vegetation feedback, Geophys. Res. Lett., 43, 6324–6331, https://doi.org/10.1002/2016GL069365, 2016. a
Lestang, T., Ragone, F., Bréhier, C. E., Herbert, C., and Bouchet, F.: Computing return times or return periods with rare event algorithms, J. Stat. Mech.-Theory E., 2018, https://doi.org/10.1088/1742-5468/aab856, 2018. a, b, c, d
Ridley, J., Gregory, J. M., Huybrechts, P., and Lowe, J.: Thresholds for irreversible decline of the Greenland ice sheet, Clim. Dynam., 35, 1065–1073, https://doi.org/10.1007/s00382-009-0646-0, 2010. a
Robinson, A., Calov, R., and Ganopolski, A.: Multistability and critical thresholds of the Greenland ice sheet, Nat. Clim. Change, 2, 429–432, https://doi.org/10.1038/nclimate1449, 2012. a
Rolland, J. and Simonnet, E.: Statistical Behaviour of Adaptive Multilevel Splitting Algorithms in Simple Models, J. Comput. Phys., 283, 541–558, https://doi.org/10.1016/j.jcp.2014.12.009, 2015. a, b, c, d, e, f
Teo, I., Mayne, C. G., Schulten, K., and Lelièvre, T.: Adaptive Multilevel Splitting Method for Molecular Dynamics Calculation of Benzamidine-Trypsin Dissociation Time, J. Chem. Theory Comput., 12, 2983–2989, https://doi.org/10.1021/acs.jctc.6b00277, 2016. a
Wang, P.: Python implementation of the Trajectory Adaptive Multilevel Sampling algorithm for rare events and improvements, Software, figshare, https://doi.org/10.6084/m9.figshare.13914353.v2, 2021a. a
Wang, P.: Python implementation of the geometric minimum action method (gMAM), Software, figshare, https://doi.org/10.6084/m9.figshare.13919642.v1, 2021b. a
Wang, P. and Castellana, D.: Dataset for “Improvements to the use of the Trajectory-Adaptive Multilevel Sampling algorithm for the study of rare events”, Dataset, figshare, https://doi.org/10.6084/m9.figshare.13918100.v1, 2021. a
Wasserman, L.: All of statistics: a concise course in statistical inference, Springer Science & Business Media, Springer-Verlag New York, 2013. a
- Abstract
- Introduction
- Methods
- Results
- Summary and discussion
- Appendix A: Trajectory-Adaptive Multilevel Sampling (TAMS) algorithm
- Appendix B: Box model for the Atlantic Meridional Ocean Circulation
- Code availability
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Methods
- Results
- Summary and discussion
- Appendix A: Trajectory-Adaptive Multilevel Sampling (TAMS) algorithm
- Appendix B: Box model for the Atlantic Meridional Ocean Circulation
- Code availability
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References






