Derivation of the entropic formula for the statistical mechanics of space plasmas

Kappa distributions describe velocities and energies of plasma populations in space plasmas. The statistical origin of these distributions is associated with the framework of nonextensive statistical mechanics. Indeed, the kappa distribution is derived by maximizing the q entropy of Tsallis, under the constraints of the canonical ensemble. However, the question remains as to what the physical origin of this entropic formulation is. This paper shows that the q entropy can be derived by adapting the additivity of energy and entropy.

1 Introduction

Space plasmas are collisionless and correlated particle systems characterized by a non-Maxwellian behavior, typically described by the formulations of kappa distributions. The origin of this vastly different statistical behavior between classical systems and space plasmas is the manifestation of correlations between the plasma particles. These systems are characterized by long-range interactions that induce correlations, resulting in a collective behavior among particles (e.g., see Jund et al., 1995; Salazar and Toral, 1999; Villain, 2008; Tsallis, 2009; Grassi, 2010; Tirnakli and Borges, 2016). The induction of any type of correlations among particles (more accurately, among particle energies or particle phase space) departs the system from thermal equilibrium to be restabilized into other stationary states out of thermal equilibrium described by kappa distributions, or combinations/superposition thereof. (Note that as we will see in Sect. 3, single kappa distributions induce a certain type of correlation, which, however, can be further generalized when a combination or superposition of kappa distributions is taken into account; e.g., see Spectral Statistics, Tsallis, 2009, Linear/Nonlinear superposition, chap. 6.2.1; Livadiotis and McComas, 2013a, Appendix A; Livadiotis, 2017a, chap. 4.3.4.)

Kappa distributions describe numerous space plasma populations. Several examples are the following: (i) the inner heliosphere, including solar wind (e.g., Maksimovic et al., 1997; Pierrard et al., 1999; Mann et al., 2002; Marsch, 2006; Zouganelis, 2008; Štverák et al., 2009; Livadiotis and McComas, 2013a; Yoon, 2014; Pierrard and Pieters, 2015; Pavlos et al., 2016), solar spectra (e.g., Dzifčáková and Dudík, 2013; Dzifčáková, et al., 2015), solar corona (e.g., Owocki and Scudder, 1983; Vocks et al., 2008; Lee et al., 2013; Cranmer, 2014), solar energetic particles (e.g., Xiao et al., 2008; Laming et al., 2013), corotating interaction regions (e.g., Chotoo et al., 2000), and related solar flares (e.g., Mann et al., 2009; Livadiotis and McComas, 2013b; Bian et al., 2014; Jeffrey et al., 2016); (ii) planetary magnetospheres, including magnetosheath (e.g., Formisano et al., 1973; Ogasawara et al., 2013), magnetopause (e.g., Ogasawara et al., 2015), magnetotail (e.g., Grabbe, 2000), ring current (e.g., Pisarenko et al., 2002), plasma sheet (e.g., Christon, 1987; Wang et al., 2003; Kletzing et al., 2003), magnetospheric substorms (e.g., Hapgood et al., 2011), aurora (e.g., Ogasawara et al., 2017), magnetospheres of giant planets, such as Jovian (e.g., Collier and Hamilton, 1995; Mauk et al., 2004), Saturnian (e.g., Dialynas et al., 2009; Livi et al., 2014; Carbary et al., 2014), Uranian (e.g., Mauk et al., 1987), and Neptunian (Krimigis et al., 1989), magnetospheres of planetary moons, such as Io (e.g., Moncuquet et al., 2002) and Enceladus (e.g., Jurac et al., 2002), and cometary magnetospheres (e.g., Broiles et al.,, 2016a, b); (iii) the outer heliosphere and the inner heliosheath (e.g., Decker and Krimigis, 2003; Decker et al., 2005; Heerikhuisen et al., 2008, 2015; Zank et al., 2010; Livadiotis et al., 2011, 2012; 2013; Livadiotis and McComas, 2011a, 2012; 2013c; Livadiotis, 2014, 2016; Fuselier et al., 2014; Zirnstein and McComas, 2015; Zank, 2015); (iv) beyond the heliosphere, including HII regions (e.g., Nicholls et al., 2012), planetary nebula (e.g., Nicholls et al., 2013; Zhang et al., 2014), and supernova magnetospheres (e.g., Raymond et al., 2010), and on cosmological scales (e.g., Hou et al., 2017); and (v) other space-plasma-related analyses (e.g., Milovanov and Zelenyi, 2000; Saito et al., 2000; Du, 2004; Yoon et al., 2006, 2012; Raadu and Shafiq, 2007; Livadiotis, 2009, 2015a, b, c, 2018; Tribeche et al., 2009; Hellberg et al., 2009; Livadiotis and McComas, 2010b, 2014; Baluku et al., 2010; Le Roux et al., 2010; Eslami et al., 2011; Kourakis et al., 2012; Randol and Christian, 2014, 2016; Varotsos et al., 2014; Fisk and Gloeckler, 2014; Viñas et al., 2014, 2015; Ourabah et al., 2015; Dos Santos et al., 2016; Nicolaou and Livadiotis, 2016). (See also the book Livadiotis, 2017a, and references therein.) Finally, it has to be noted that the kappa distributions and its associated statistical mechanics have been applied in a variety of disciplines other than space and plasma physics. A few examples are the following: in sociometry, e.g., the internet (Abe and Suzuki, 2003) and in citation networks of scientific papers (Tsallis and De Albuquerque, 2000) and urban agglomeration (Malacarne et al., 2001); in linguistics (Montemurro, 2001); in economics (Borland, 2002); in biochemistry (Andricioaei and Straub, 1996); in applied statistics (Habeck et al., 2005); in nonlinear dynamics (Borges et al., 2002); in physical chemistry (Livadiotis, 2009); and in ecology (Livadiotis et al., 2015, 2016).

Empirical kappa distributions were introduced in mid-1960s by Binsack (1966), Olbert (1968), and Vasyliũnas (1968), while their connection with statistical mechanics was shown and studied in detail about half a century later (see Livadiotis and McComas, 2009, and references therein). In particular, the statistical origin of these distributions is now widely accepted to be determined within the framework of nonextensive statistical mechanics (Tsallis, 2009). This is a consistent generalization of the classical statistical mechanics, which is based on a monoparametric (q index) entropic formula (Tsallis, 1988). The theoretical q exponential distribution, which results from the maximization of entropy in the canonical ensemble, has the same formulation as the empirical kappa distribution; the two distributions are identical under the transformation of their characteristic indices ($q=\mathrm{1}+\mathrm{1}/\mathit{\kappa }$).

Though a consistent connection of the mathematical model of kappa distributions has been attained with the physical means of entropy maximization, this does not precisely answer the main question regarding the origin of these distributions. We have only shifted the modeling from the distributions to the entropic formulation. Therefore, we may understand now that the statistical origin of kappa distributions is given by the Tsallis entropy maximization in the canonical ensemble, but still, the origin of this specific entropic formulation remains unknown.

Certainly, there are various mechanisms responsible for generating kappa distributions in space and other plasmas, for example, the presence of pickup ions (Livadiotis and McComas, 2010a, 2011a) or weak turbulence (Yoon et al., 2012; Yoon, 2014). Moreover, kappa distributions belong to the framework of nonextensive statistical mechanics. Thus, once a kappa distribution is generated and stabilized into a plasma population, the whole “tool package” of nonextensive statistical mechanics is applicable for describing the statistical physics of this population; for instance, the entropy is given by the Tsallis formulation, while the temperature can be determined by the mean kinetic energy.

Here, we do not argue which mechanisms generate kappa distributions in space plasmas, rather the physical reasons that these distributions sustain themselves in space plasmas once generated. The typical answer is that this is an effect of the presence and preservation of correlations in the collisionless environment that governs space plasmas. (For particle systems such as space plasmas, collisions can destroy correlations, and thus, their collective behavior.) The collisionless environment conserves the energy. Moreover, weakly coupled plasmas (mutual electron and ion potential energy is small compared to the average kinetic energy) can be described as ideal gases. Interparticle energy terms can be ignored, leading to the additivity of energy: the energy of a multi-particle state is the sum of the energies of all the one-particle states involved. On the other hand, the preservation of local correlations among particles creates a conceptual separation of particles in correlation clusters. Debye spheres are correlation clusters that may include up to trillions of particles since space plasmas are weakly coupled (Bryant, 1996; Rubab and Murtaza, 2006; Gougam and Tribeche, 2011; Livadiotis and McComas, 2014). This structure can lead to the additivity of entropy: the entropy of a multi-particle state is the sum of the entropies of all the one-particle states involved. (Note that ideal gases are considered to have (i) zero interparticle interactions, and (ii) zero particle correlations. While ideal gases are characterized by short-range interactions that cannot induce correlations among particles, space plasmas have interactions weak enough to be negligible but with a long enough range that correlations can be induced.)

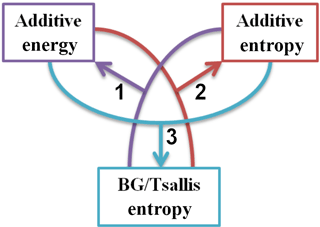
Figure 1 The infographic indicates the following triplet of concepts: (i) additive energy, (ii) additive entropy, and (iii) BG or Tsallis entropic formulation. Given any two out of the three features, the third can be derived. It is already known that BG or Tsallis entropic formulations can lead to additive entropy if the energy is also additive (red arrow 2). In the same way, it can be shown that these entropic formulations can lead to additive energy if the entropy is additive (purple arrow 1). The objective here is to show that the entropic formula can be derived from the additivity of energy and entropy (blue arrow 3).

The purpose of this paper is to show that there is a deeper connection of Tsallis q entropy and space plasmas: namely, we will show that two simple first principles, such as the additive energy and additive entropy, which apply to plasma particle populations, are sufficient for indicating the specific formula of q entropy (Fig. 1). Therefore, the main objective of this work is to demonstrate the theory which determines that the entropic form given by the q-entropy formula proposed originally by Tsallis (1988) follows from certain assumptions regarding the (microscopic) state of the system. The importance of this discussion for the (space) plasma physics community resides mostly in the fact that the kappa velocity/energy distribution functions, ubiquitously observed in space and astrophysical environments, can be derived from the maximization of the q entropy, under the constraints of a canonical ensemble.

In Sect. 2, we describe the physical motive of this paper in detail. In Sect. 3, we show in detail a similar property for both the entropic formalisms of Boltzmann–Gibbs (BG) and Tsallis: the entropy is non-additive in general for some arbitrary probability distribution, but it can become additive specifically for the canonical probability distribution (the one that maximizes the corresponding entropy). In Sect. 4, we show how we can determine the entropic formula appropriate for describing the plasma particle populations, simply by setting two first principles' properties, obvious for collisionless plasmas: energy and entropy are additive, at least macroscopically. Finally, Sect. 5 briefly summarizes the conclusions.

2 Physical motive

Classical BG statistical mechanics characterizes systems with no correlations among particle velocities or energies. Therefore, the joint two-particle probability distribution can be expressed as the product of the one-particle identical and independent discrete distributions, i.e., labeling the two particles with A and B, $p_{ij}^{\mathrm{A}+\mathrm{B}}=p_i^{\mathrm{A}}\cdot p_j^{\mathrm{B}}$. Hereafter, we consider a particle system described by a discrete energy spectrum $\mathit{\{}{\mathit{\epsilon }}_k{\mathit{\}}}_{k=\mathrm{1}}^W$, which is associated with a discrete probability distribution $\mathit{\{}{p}_k{\mathit{\}}}_{k=\mathrm{1}}^W$. The same semantics is used when the system is separated in two subsystems, A and B, where the two-particle distribution describes a two-particle state, with one particle at each subsystem. The logarithm of the probability is an additive function, $\ln p_{ij}^{\mathrm{A}+\mathrm{B}}=\ln p_i^{\mathrm{A}}+\ln p_j^{\mathrm{B}}$, from which we obtain the additivity of entropy (here the BG entropy), $S^{\mathrm{A}+\mathrm{B}}=S^{\mathrm{A}}+S^{\mathrm{B}}$. For special cases, however, where the independence relationship does not apply, $p_{ij}^{\mathrm{A}+\mathrm{B}}\ne p_i^{\mathrm{A}}\cdot p_j^{\mathrm{B}}$, the entropy is non-additive, $S^{\mathrm{A}+\mathrm{B}}\ne S^{\mathrm{A}}+S^{\mathrm{B}}$. The logical reciprocant to the statements above is provided by the uniqueness theorem of Shannon (1948) and Khinchin (1957) that showed that under the assumption of the additivity of entropy (and other basic properties of entropy), the sufficient and necessary entropic form is given by the BG formula.

Nonextensive statistical mechanics characterizes systems with correlations among particles, $p_{ij}^{\mathrm{A}+\mathrm{B}}\ne p_i^{\mathrm{A}}\cdot p_j^{\mathrm{B}}$. For special systems, however, where the independence relationship still applies, the entropy (here the q entropy) is non-additive, $S^{\mathrm{A}+\mathrm{B}}\ne S^{\mathrm{A}}+S^{\mathrm{B}}$; in particular, a square, nonlinear term is added to the summation, $S^{\mathrm{A}+\mathrm{B}}=S^{\mathrm{A}}+S^{\mathrm{B}}+(\mathrm{1}-q)S^{\mathrm{A}}{S}^{\mathrm{B}}$, for some value of the entropic parameter q (where we set the Boltzmann constant k_B to 1). Note that the logical reciprocant also exists for this case, as shown by Dos Santos (1997) and Abe (2000); namely, under the assumption of the non-additive property mentioned (and other basic properties of entropy), the sufficient and necessary entropic form is given by the q entropic formula of Tsallis (1988).

Another property that is related with the additivity but is even more subtle and difficult to ascertain is the extensivity of the entropy. A non-additive entropy may be assumed to be also nonextensive, but it is the inverse assumption that is always correct; i.e., nonextensivity implies non-additivity. Nevertheless, certain correlations, expressed by the probability relationship $p_{ij}^{\mathrm{A}+\mathrm{B}}=g^{-\mathrm{1}}\left[g\right(p_i^{\mathrm{A}})+g(p_j^{\mathrm{B}}\left)\right]$ for a function g, can make the Tsallis entropy additive, and thus, recover its extensivity (e.g., Tsallis et al., 2005; Ruseckas, 2015). (Note that in his book, Tsallis (2009) goes to large lengths to show that it is possible to find systems for which the BG entropy is not extensive. On the other hand, he argues that there are certain systems for which the entropic form can be extensive, for certain values of the entropic index q. In fact, he mentions in the preface that the term “nonextensive entropy” is somewhat incorrect in this sense, but that it stuck for historical reasons.)

The two statistical formalisms, classical BG and Tsallis nonextensive, have the common property that their entropy becomes additive for a specific function g in the relationship $p_{ij}^{\mathrm{A}+\mathrm{B}}=g^{-\mathrm{1}}\left[g\right(p_i^{\mathrm{A}})+g(p_j^{\mathrm{B}}\left)\right]$, that is, g(x)∝ln (x) and $g\left(x\right)\propto (x^{q-\mathrm{1}}-\mathrm{1})/(q-\mathrm{1})$, respectively (the latter is related to the q deformed logarithm; see Silva et al., 1998; Yamano, 2002).

It is important that the above probability relationship is a characteristic feature of the canonical probability distribution in both the formalisms. In other words, the probability distribution that maximizes the BG entropy under the constraints of the canonical ensemble conforms to the correlations expressed by g(x)∝ln (x) or $p_{ij}^{\mathrm{A}+\mathrm{B}}=p_i^{\mathrm{A}}\cdot p_j^{\mathrm{B}}$, which simply means zero correlation (due to the factorization of the exponentials; Livadiotis and McComas, 2011b) that makes the entropy additive. Also, the probability distribution that maximizes the Tsallis entropy under the same constraints (i.e., q exponential or kappa distribution) conforms to the specific correlations expressed by $g\left(x\right)\propto (x^{q-\mathrm{1}}-\mathrm{1})/(q-\mathrm{1})$ or $(p_{ij}^{\mathrm{A}+\mathrm{B}}{)}^{q-\mathrm{1}}=(p_i^{\mathrm{A}}{)}^{q-\mathrm{1}}+(p_j^{\mathrm{B}}{)}^{q-\mathrm{1}}-\mathrm{1}$, which again makes the entropy additive. In Sect. 3 we show this similar property of the two statistical formalisms in detail.

Then, we may ask the following question: is the property of BG and Tsallis entropies described above a general feature of any physically meaningful entropic function? Or can we reverse the question, and ask which specific entropic function follows the above properties? It will be really intriguing if we can determine the entropic formula appropriate for describing the plasma particle populations, simply by setting the following two first principles' properties: (1) additive energy, (2) additive entropy; i.e., the probability distribution derived by maximizing the entropy under the constraints of the canonical ensemble makes the entropy additive. This will be the main purpose of this paper and will be examined in Sect. 4.

3 Canonical ensemble distributions with additive energy lead to additive entropy

3.1 The Gibbs' path

The Gibbs' path (1902) for the maximization of the entropy $S(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)$ under the constraints of a canonical ensemble (i.e., (i) normalization $\mathrm{1}={\sum }_{k=\mathrm{1}}^W{p}_k$ and (ii) fixed internal energy $U={\sum }_{k=\mathrm{1}}^W{p}_k{\mathit{\epsilon }}_k$) involves maximizing the functional

$$\begin{array}{ll}{\displaystyle }G(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)& {\displaystyle }=S(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)+{\mathit{\lambda }}_{\mathrm{1}}{\sum }_{k=\mathrm{1}}^W{p}_k\\ \text{(1)}& {\displaystyle }& {\displaystyle }+{\mathit{\lambda }}_{\mathrm{2}}{\sum }_{k=\mathrm{1}}^W{p}_k{\mathit{\epsilon }}_k.\end{array}$$

Next, we examine the BG and Tsallis entropic formulations.

3.2 BG entropy

First, we start from the classical case of BG entropy

$$\begin{array}{}\text{(2)}& S(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)=-\sum _{k=\mathrm{1}}^W{p}_k\ln \left(p_k\right),\end{array}$$

where we ignored the Boltzmann constant k_B for simplicity. Then, setting $(\partial /\partial p_j)G(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)=\mathrm{0}$ to

$$\begin{array}{ll}{\displaystyle }G(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)=& {\displaystyle }-\sum _{k=\mathrm{1}}^W{p}_k\ln \left(p_k\right)+{\mathit{\lambda }}_{\mathrm{1}}{\sum }_{k=\mathrm{1}}^W{p}_k\\ \text{(3)}& {\displaystyle }& {\displaystyle }+{\mathit{\lambda }}_{\mathrm{2}}{\sum }_{k=\mathrm{1}}^W{p}_k{\mathit{\epsilon }}_k,\end{array}$$

we find

$$\begin{array}{}\text{(4)}& p_j\left({\mathit{\epsilon }}_j\right)=\exp ({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})\cdot \exp \left({\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_j\right).\end{array}$$

We may write Eq. (2) in a logarithmic form, $\ln p_j={\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_j+{\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}$. Then, we separate the particle system into two parts, A and B, so that each part is a new subsystem for which Eq. (2) holds:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }\ln p_i^{\mathrm{A}}={\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_i^{\mathrm{A}}+{\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}\text{and}\ln p_j^{\mathrm{B}}={\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_j^{\mathrm{B}}+{\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}.\end{array}$$

The whole system is characterized by the joint probability, $p_{ij}^{\mathrm{A}+\mathrm{B}}$, meaning the probability of a particle in the subsystem A of residing in the state i and a particle in the subsystem B of residing in the state j. This is related with the energy ${\mathit{\epsilon }}_{ij}^{\mathrm{A}+\mathrm{B}}$ of the two-particle state,

$$\begin{array}{}\text{(6)}& \ln p_{ij}^{\mathrm{A}+\mathrm{B}}={\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_{ij}^{\mathrm{A}+\mathrm{B}}+{\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}.\end{array}$$

Trivially, the energy of the two-particle state energy ${\mathit{\epsilon }}_{ij}^{\mathrm{A}+\mathrm{B}}$ equals the summation of the energy of each particle (since no interparticle force is considered); i.e., the system's energy is additive:

$$\begin{array}{}\text{(7)}& {\mathit{\epsilon }}_{ij}^{\mathrm{A}+\mathrm{B}}={\mathit{\epsilon }}_i^{\mathrm{A}}+{\mathit{\epsilon }}_j^{\mathrm{B}}.\end{array}$$

Hence, by eliminating energies from Eqs. (5) and (6), we find

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\ln p_{ij}^{\mathrm{A}+\mathrm{B}}+({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})={\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_i^{\mathrm{A}}+({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})+{\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_j^{\mathrm{B}}+({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})\\ \text{(8)}& {\displaystyle }& {\displaystyle }=\ln p_i^{\mathrm{A}}+\ln p_j^{\mathrm{B}}\text{or}\text{(9)}& {\displaystyle }& {\displaystyle }{p}_{ij}^{\mathrm{A}+\mathrm{B}}=p_i^{\mathrm{A}}\cdot p_j^{\mathrm{B}}\cdot e^{-({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})}.\end{array}$$

At this point we recall that the Lagrange multipliers, λ₁ and λ₂, are related with the partition function $Z=e^{-({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})}$ and the inverse temperature $\mathit{\beta }=-{\mathit{\lambda }}_{\mathrm{2}}$, respectively, and they are not necessarily equal for the two subsystems A and B, or the whole system A + B. Nevertheless, the logarithm of the partition function or (λ₁−1) is an extensive parameter, i.e., $({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}{)}^{\mathrm{A}+\mathrm{B}}=({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}{)}^{\mathrm{A}}+({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}{)}^{\mathrm{B}}$, while the temperature is not an extensive parameter and can be considered the same: ${\mathit{\lambda }}_{\mathrm{2}}^{\mathrm{A}+\mathrm{B}}={\mathit{\lambda }}_{\mathrm{2}}^{\mathrm{A}}={\mathit{\lambda }}_{\mathrm{2}}^{\mathrm{B}}$. Then, instead of Eqs. (8) and (9), we obtain

$$\begin{array}{ll}{\displaystyle }\ln p_{ij}^{\mathrm{A}+\mathrm{B}}& {\displaystyle }={\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_{ij}^{\mathrm{A}+\mathrm{B}}+({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}{)}^{\mathrm{A}+\mathrm{B}}\\ {\displaystyle }& {\displaystyle }={\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_i^{\mathrm{A}}+({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}{)}^{\mathrm{A}}+{\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_j^{\mathrm{B}}+({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}{)}^{\mathrm{B}}\\ \text{(10)}& {\displaystyle }& {\displaystyle }=\ln p_i^{\mathrm{A}}+\ln p_j^{\mathrm{B}},\end{array}$$

which clearly shows that the canonical probabilities are independent:

$$\begin{array}{}\text{(11)}& \ln \left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)=\ln \left(p_i^{\mathrm{A}}\right)+\ln \left(p_j^{\mathrm{B}}\right)\Rightarrow p_{ij}^{\mathrm{A}+\mathrm{B}}=p_i^{\mathrm{A}}\cdot p_j^{\mathrm{B}}.\end{array}$$

Equation (6) indicates that the result in Eq. (6) can be obtained simply by setting λ₁=1. Certainly, this restricts the generality, but it can be used as a trick to simplify the calculations. Furthermore, we can easily obtain the additivity of entropy. Indeed, applying the operator ${\sum }_{i=\mathrm{1}}^W{\sum }_{j=\mathrm{1}}^W{p}_{ij}^{\mathrm{A}+\mathrm{B}}\times$ to both sides of Eq. (6), we obtain

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{p}_{ij}^{\mathrm{A}+\mathrm{B}}\ln p_{ij}^{\mathrm{A}+\mathrm{B}}=p_{ij}^{\mathrm{A}+\mathrm{B}}\ln p_i^{\mathrm{A}}+p_{ij}^{\mathrm{A}+\mathrm{B}}\ln p_j^{\mathrm{B}}\\ {\displaystyle }& {\displaystyle }\Rightarrow -\sum _{i=\mathrm{1}}^W\sum _{j=\mathrm{1}}^W{p}_{ij}^{\mathrm{A}+\mathrm{B}}\ln p_{ij}^{\mathrm{A}+\mathrm{B}}=-\sum _{i=\mathrm{1}}^W{p}_i^{\mathrm{A}}\ln \left(p_i^{\mathrm{A}}\right)\\ \text{(12)}& {\displaystyle }& {\displaystyle }-\sum _{j=\mathrm{1}}^W{p}_j^{\mathrm{B}}\ln \left(p_j^{\mathrm{B}}\right)\end{array}$$

because ${\sum }_{j=\mathrm{1}}^W{p}_{ij}^{\mathrm{A}+\mathrm{B}}=p_i^{\mathrm{A}}$ and ${\sum }_{i=\mathrm{1}}^W{p}_{ij}^{\mathrm{A}+\mathrm{B}}=p_j^{\mathrm{B}}$. Hence, we arrive at the additivity of the entropy of the system to the entropies of the subsystems,

$$\begin{array}{}\text{(13)}& S^{\mathrm{A}+\mathrm{B}}=S^{\mathrm{A}}+S^{\mathrm{B}}.\end{array}$$

3.3 Tsallis entropy

Next, we continue with the Tsallis q entropy,

$$\begin{array}{ll}{\displaystyle }S(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)& {\displaystyle }={\displaystyle \frac{\mathrm{1}-\mathit{\phi }(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)}{q-\mathrm{1}}}\\ \text{(14)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{q-\mathrm{1}}}\cdot \sum _{k=\mathrm{1}}^W\left(p_k-p_k^q\right),\end{array}$$

(e.g., Havrda and Charvát, 1967; Tsallis, 1988) where the argument φ is defined by

$$\begin{array}{}\text{(15)}& \mathit{\phi }(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)=\sum _{k=\mathrm{1}}^W{p}_k^q.\end{array}$$

Again, the maximization of the entropy under the constraints of the canonical ensemble involves maximizing the functional

$$\begin{array}{ll}\text{(16)}& {\displaystyle }G(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{q-\mathrm{1}}}\cdot \sum _{k=\mathrm{1}}^W\left(p_k-p_k^q\right)+{\mathit{\lambda }}_{\mathrm{1}}{\sum }_{k=\mathrm{1}}^W{p}_k{\displaystyle }& {\displaystyle }+{\mathit{\lambda }}_{\mathrm{2}}{\sum }_{k=\mathrm{1}}^W{p}_k{\mathit{\epsilon }}_k.\end{array}$$

Note that for simplicity we do not use the formulation of escort distributions (Beck and Schlogl, 1993). The dyadic formalism of ordinary/escort distributions is of fundamental importance in modern nonextensive statistical mechanics (Livadiotis, 2017a; chap. 1). It has been shown that this dyadic formalism of distributions can be avoided in order to simplify the theory, but it leads to a dyadic formulation of entropy (Livadiotis, 2017b).

Hence, $(\partial /\partial p_j)G(p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\dots },p_W)=\mathrm{0}$ gives

$$\begin{array}{ll}\text{(17a)}& {\displaystyle }{p}_j\left({\mathit{\epsilon }}_j\right)=& {\displaystyle }{\left[\mathrm{1}+(\mathrm{1}-q^{-\mathrm{1}})\cdot ({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})\right]}^{\frac{q^{-\mathrm{1}}}{\mathrm{1}-q^{-\mathrm{1}}}}{\displaystyle }& {\displaystyle }\times {\left[\mathrm{1}+(\mathrm{1}-q^{-\mathrm{1}})\cdot {\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_j}{\mathrm{1}+(\mathrm{1}-q^{-\mathrm{1}})\cdot ({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})}}\right]}^{\frac{q^{-\mathrm{1}}}{\mathrm{1}-q^{-\mathrm{1}}}}\end{array}$$

or

$$\begin{array}{}\text{(17b)}& {\displaystyle }{\displaystyle }{p}_j\left({\mathit{\epsilon }}_j\right)={\exp }_{q^{-\mathrm{1}}}^{q^{-\mathrm{1}}}({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})\cdot {\exp }_{q^{-\mathrm{1}}}^{q^{-\mathrm{1}}}\left[{\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_j}{{\mathrm{1}}_{q^{-\mathrm{1}}}({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})}}\right],\end{array}$$

which reflects a generalization of Eq. (2). We used the Q-deformed exponential function, and its inverse, the Q-logarithm function (Silva et al., 1998; Yamano, 2002), defined by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\exp }_Q\left(x\right)={\left[\mathrm{1}+(\mathrm{1}-Q)\cdot x\right]}_{+}^{-\frac{\mathrm{1}}{Q-\mathrm{1}}},\\ \text{(18a)}& {\displaystyle }& {\displaystyle }{\ln }_Q\left(x\right)={\displaystyle \frac{\mathrm{1}-x^{\mathrm{1}-Q}}{Q-\mathrm{1}}}.\end{array}$$

We also used the Q-deformed “unity function” (Livadiotis and McComas, 2009), defined by

$$\begin{array}{}\text{(18b)}& {\displaystyle }{\displaystyle }{\mathrm{1}}_Q\left(x\right)={\left[\mathrm{1}+(\mathrm{1}-Q)\cdot x\right]}_{+}.\end{array}$$

The subscript “+” in […]₊ denotes the cut-off condition, where exp _Q(x) becomes zero if its base […] is non-positive. Therefore, Eq. (9b) leads to

$$\begin{array}{ll}\text{(19)}& {\displaystyle }& {\displaystyle }{p}_j^{q-\mathrm{1}}=\mathrm{1}+(\mathrm{1}-q^{-\mathrm{1}})\cdot ({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1})+(\mathrm{1}-q^{-\mathrm{1}})\cdot {\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_j,{\displaystyle }& {\displaystyle \frac{\mathrm{1}-p_j^{q-\mathrm{1}}}{q^{-\mathrm{1}}-\mathrm{1}}}={\ln }_{q^{-\mathrm{1}}}\left(p_j^q\right)=-q\cdot {\ln }_q\left(p_j^{-\mathrm{1}}\right)\\ \text{(20)}& {\displaystyle }& {\displaystyle }={\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_j+({\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}).\end{array}$$

Dividing again the whole system into two subsystems, A and B, using the additivity of energy, and setting λ₁=1, the independence relation (Eq. 6) is generalized to

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\ln }_q\left[{\left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)}^{-\mathrm{1}}\right]={\ln }_q\left[{\left(p_i^{\mathrm{A}}\right)}^{-\mathrm{1}}\right]+{\ln }_q\left[{\left(p_j^{\mathrm{B}}\right)}^{-\mathrm{1}}\right]\\ \text{(21)}& {\displaystyle }& {\displaystyle }\Rightarrow {\left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)}^{q-\mathrm{1}}={\left(p_i^{\mathrm{A}}\right)}^{q-\mathrm{1}}+{\left(p_j^{\mathrm{B}}\right)}^{q-\mathrm{1}}-\mathrm{1},\end{array}$$

which is sometimes called the q independence relationship (Umarov et al., 2008). Then, we apply the operator ${\sum }_{i=\mathrm{1}}^W{\sum }_{j=\mathrm{1}}^W{p}_{ij}^{\mathrm{A}+\mathrm{B}}\times$,

$$\begin{array}{ll}{\displaystyle }{\sum }_{i=\mathrm{1}}^W{\sum }_{j=\mathrm{1}}^W{\left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)}^q& {\displaystyle }={\sum }_{i=\mathrm{1}}^W{\left(p_i^{\mathrm{A}}\right)}^q+{\sum }_{j=\mathrm{1}}^W{\left(p_j^{\mathrm{B}}\right)}^q\\ \text{(22)}& {\displaystyle }& {\displaystyle }-\mathrm{1}\Rightarrow {\mathit{\phi }}^{\mathrm{A}+\mathrm{B}}={\mathit{\phi }}^{\mathrm{A}}+{\mathit{\phi }}^{\mathrm{B}}-\mathrm{1},\end{array}$$

and using the entropic formula (Eq. 8), we end up with the additivity of entropy, as shown in Eq. (7).

Note that the additivity leads to the extensivity: the additivity for a function f is expressed by $f(\mathrm{A}+\mathrm{B})=f\left(\mathrm{A}\right)+f\left(\mathrm{B}\right)$, or considering N different subsystems,

$$\begin{array}{}\text{(23a)}& {\displaystyle }{\displaystyle }f\left({\bigcup }_{n=\mathrm{1}}^N{\mathrm{A}}_n\right)={\sum }_{n=\mathrm{1}}^{N}f\left({\mathrm{A}}_n\right),\end{array}$$

while the extensivity is expressed by

$$\begin{array}{}\text{(23b)}& {\displaystyle }{\displaystyle }f\left({\bigcup }_{n=\mathrm{1}}^N{\mathrm{A}}_{\mathrm{0}}\right)=N\cdot f\left({\mathrm{A}}_{\mathrm{0}}\right).\end{array}$$

Therefore, the canonical probability distribution, the one that maximizes the entropy under the constraints of a canonical ensemble, makes the entropy additive (and therefore extensive) if the energy is additive. Several special conditions can simplify this result, e.g., constant Lagrange constraints with λ₁=1 (i.e., independent of the probability distribution). This is, however, the case for both the entropic formulation of classical BG and Tsallis nonextensive statistical mechanics.

Next, we reverse the problem and seek to find the specific entropic formula for which both the energy and entropy are additive.

4 Additive energy and entropy leads to Tsallis entropic formalism

The general entropic form is still function of the probabilities: $S=S\left(\mathit{\right\{}{p}_k{\mathit{\}}}_{k=\mathrm{1}}^W)$. Then, its derivative with respect to any of the probability components, for example the ith, is also a function of all of these components, i.e., $\partial S/\partial p_i=F_i\left(\mathit{\right\{}{p}_k{\mathit{\}}}_{k=\mathrm{1}}^W)$, for any i: $\mathrm{1},\mathrm{\dots },W$. However, the second constraint (i.e., fixed internal energy) of the canonical ensemble connects the ith entropic derivative to a function h_i of the ith energy, ε_i, namely, $\partial S/\partial p_i=h_i\left({\mathit{\epsilon }}_i\right)$. On the other hand, the canonical probability distribution derived from the entropy maximization constitutes an expression of the ith probability component with some invertible function g of the ith energy, p_i=g(ε_i). Therefore, we conclude that $\partial S/\partial p_i=F_i\left(p_i\right)$, where $F_i=h_i\circ g^{-\mathrm{1}}$; in other words, the entropy can be factorized as a summation of functions of each probability component, $S={\sum }_{k=\mathrm{1}}^W{f}_k\left(p_k\right)$, where we set $f_i\left(p_i\right)=\int F_i\left(p_i\right)d{p}_i$. Finally, we consider that none of the states ($k=\mathrm{1},\mathrm{\dots },W$) should have a special effect on the entropy; i.e., each state “weights” the same, so the entropic functional $S=S\left(\mathit{\right\{}{p}_k{\mathit{\}}}_{k=\mathrm{1}}^W)$ should be symmetric to any permutation of each components, e.g., $S=S(\mathrm{\dots },p_k,\mathrm{\dots },p_{\mathrm{\ell }},\mathrm{\dots })=S(\mathrm{\dots },p_{\mathrm{\ell }},\mathrm{\dots },p_k,\mathrm{\dots })$ (i.e., the entropy is invariant under any relabeling of the states). This leads to f_k=f; hence, considering (1) entropy maximization and (2) no weighting, we obtain

$$\begin{array}{}\text{(24a)}& {\displaystyle }{\displaystyle }S={\sum }_{k=\mathrm{1}}^{W}f\left(p_k\right).\end{array}$$

For example, in the cases of Boltzmann (Eq. 1) and Tsallis (Eq. 8) entropies, the function f is respectively given by

$$\begin{array}{}\text{(24b)}& {\displaystyle }{\displaystyle }f\left(x\right)=-x\ln \left(x\right)\text{and}f\left(x\right)=(x-x^q)/(q-\mathrm{1}).\end{array}$$

The maximization of entropy under the constraints of a canonical ensemble, i.e., $\mathrm{1}={\sum }_{k=\mathrm{1}}^W{p}_k$ and $U={\sum }_{k=\mathrm{1}}^W{p}_k{\mathit{\epsilon }}_k$, involves maximizing the functional $G\left(\mathit{\right\{}{p}_k{\mathit{\}}}_{k=\mathrm{1}}^W)={\sum }_{k=\mathrm{1}}^{W}f(p_k)+{\mathit{\lambda }}_{\mathrm{1}}{\sum }_{k=\mathrm{1}}^W{p}_k+{\mathit{\lambda }}_{\mathrm{2}}{\sum }_{k=\mathrm{1}}^W{p}_k{\mathit{\epsilon }}_k$. Hence, setting $\partial G\left(\mathit{\right\{}{p}_k{\mathit{\}}}_{k=\mathrm{1}}^W)/\partial p_i=\mathrm{0}$, we obtain

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }F\left(p_i\right)+{\mathit{\lambda }}_{\mathrm{1}}+{\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_i=\mathrm{0},\text{or}{p}_i\left({\mathit{\epsilon }}_i\right)=F^{-\mathrm{1}}(-{\mathit{\lambda }}_{\mathrm{1}}-{\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_i),\\ \text{(25)}& {\displaystyle }& {\displaystyle }\text{with}F\left(x\right)\equiv f^{\prime }\left(x\right).\end{array}$$

We now consider two systems A and B, with respective energy spectra $\mathit{\{}{\mathit{\epsilon }}_i^{\mathrm{A}}{\mathit{\}}}_{i=\mathrm{1}}^W$ and $\mathit{\{}{\mathit{\epsilon }}_j^{\mathrm{B}}{\mathit{\}}}_{j=\mathrm{1}}^W$, associated with the discrete probability distributions $\mathit{\{}{p}_i^{\mathrm{A}}{\mathit{\}}}_{i=\mathrm{1}}^W$ and $\mathit{\{}{p}_j^{\mathrm{B}}{\mathit{\}}}_{j=\mathrm{1}}^W$. The total system A + B has an energy spectrum $\mathit{\{}{\mathit{\epsilon }}_{ij}^{\mathrm{A}+\mathrm{B}}{\mathit{\}}}_{i,j=\mathrm{1}}^W$, associated with the joint probability distribution $\mathit{\{}{p}_{ij}^{\mathrm{A}+\mathrm{B}}{\mathit{\}}}_{i,j=\mathrm{1}}^W$. The probability distributions $\mathit{\{}{p}_i^{\mathrm{A}}{\mathit{\}}}_{i=\mathrm{1}}^W$ and $\mathit{\{}{p}_j^{\mathrm{B}}{\mathit{\}}}_{j=\mathrm{1}}^W$ are marginal of the joint distribution, i.e., ${\sum }_{j=\mathrm{1}}^W{p}_{ij}^{\mathrm{A}+\mathrm{B}}=p_i^{\mathrm{A}}$ and ${\sum }_{i=\mathrm{1}}^W{p}_{ij}^{\mathrm{A}+\mathrm{B}}=p_j^{\mathrm{B}}$. As we will find further below, the joint probability can be expressed as a function of the marginal probabilities, $p_{ij}^{\mathrm{A}+\mathrm{B}}=H(p_i^{\mathrm{A}},p_j^{\mathrm{B}})$. On the other hand, the relation between the joint energies ${\mathit{\epsilon }}_{ij}^{\mathrm{A}+\mathrm{B}}$ is rather trivial to be derived: particles in A with energy ${\mathit{\epsilon }}_i^{\mathrm{A}}$ and particles in B with energy ${\mathit{\epsilon }}_j^{\mathrm{B}}$ ensemble the particles in A + B with energy ${\mathit{\epsilon }}_{ij}^{\mathrm{A}+\mathrm{B}}={\mathit{\epsilon }}_i^{\mathrm{A}}+{\mathit{\epsilon }}_j^{\mathrm{B}}$. Trivially, the same additivity holds for their mean values – the internal energies:

$$\begin{array}{ll}{\displaystyle }{U}^{\mathrm{A}+\mathrm{B}}& {\displaystyle }=\sum _{i,j}{p}_{ij}^{\mathrm{A}+\mathrm{B}}{\mathit{\epsilon }}_{ij}^{\mathrm{A}+\mathrm{B}}=\sum _{i,j}{p}_{ij}^{\mathrm{A}+\mathrm{B}}{\mathit{\epsilon }}_i^{\mathrm{A}}+\sum _{i,j}{p}_{ij}^{\mathrm{A}+\mathrm{B}}{\mathit{\epsilon }}_j^{\mathrm{B}}\\ \text{(26)}& {\displaystyle }& {\displaystyle }=\sum _i{p}_i^{\mathrm{A}}{\mathit{\epsilon }}_i^{\mathrm{A}}+\sum _j{p}_j^{\mathrm{B}}{\mathit{\epsilon }}_j^{\mathrm{B}}=U^{\mathrm{A}}+U^{\mathrm{B}}.\end{array}$$

Now, the probability distributions are related to their energies, according to Eq. (5). According to Eq. (25), we have

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }F\left(p_i^{\mathrm{A}}\right)+{\mathit{\lambda }}_{\mathrm{1}}+{\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_i^{\mathrm{A}}=\mathrm{0},F\left(p_j^{\mathrm{B}}\right)+{\mathit{\lambda }}_{\mathrm{1}}+{\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_j^{\mathrm{B}}=\mathrm{0},\\ \text{(27)}& {\displaystyle }& {\displaystyle }F\left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)+{\mathit{\lambda }}_{\mathrm{1}}+{\mathit{\lambda }}_{\mathrm{2}}{\mathit{\epsilon }}_{ij}^{\mathrm{A}+\mathrm{B}}=\mathrm{0},\end{array}$$

and due to the additivity of energies, we obtain

$$\begin{array}{}\text{(28)}& F\left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)-{\mathit{\lambda }}_{\mathrm{1}}=F\left(p_i^{\mathrm{A}}\right)+F\left(p_j^{\mathrm{B}}\right).\end{array}$$

Again, the Lagrange constants, λ₁ and λ₂, are considered to be independent of the probability distribution. Setting $\stackrel{\mathrm{̃}}{F}\equiv \frac{\mathrm{1}}{-{\mathit{\lambda }}_{\mathrm{1}}}F$, Eq. (11) becomes

$$\begin{array}{ll}\text{(29)}& {\displaystyle }& {\displaystyle }\left[\stackrel{\mathrm{̃}}{F}\left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)-\mathrm{1}\right]=\left[\stackrel{\mathrm{̃}}{F}\left(p_i^{\mathrm{A}}\right)-\mathrm{1}\right]+\left[\stackrel{\mathrm{̃}}{F}\left(p_j^{\mathrm{B}}\right)-\mathrm{1}\right],\text{or},{\displaystyle }& {\displaystyle }{p}_{ij}^{\mathrm{A}+\mathrm{B}}=H(p_i^{\mathrm{A}},p_j^{\mathrm{B}}),\\ \text{(30)}& {\displaystyle }& {\displaystyle }\mathrm{\text{with}}H(x,y)\equiv {\stackrel{\mathrm{̃}}{F}}^{-\mathrm{1}}\left[\stackrel{\mathrm{̃}}{F}\left(x\right)+\stackrel{\mathrm{̃}}{F}\left(y\right)-\mathrm{1}\right].\end{array}$$

Then, we apply ${\sum }_{i=\mathrm{1}}^W{\sum }_{j=\mathrm{1}}^W{p}_{ij}^{\mathrm{A}+\mathrm{B}}\times$ to both sides of Eq. (29):

$$\begin{array}{ll}{\displaystyle }\sum _{i,j=\mathrm{1}}^W\left[\stackrel{\mathrm{̃}}{F}\left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)-\mathrm{1}\right]& {\displaystyle }{p}_{ij}^{\mathrm{A}+\mathrm{B}}=\sum _{i=\mathrm{1}}^W\left[\stackrel{\mathrm{̃}}{F}\left(p_i^{\mathrm{A}}\right)-\mathrm{1}\right]\sum _{j=\mathrm{1}}^W{p}_{ij}^{\mathrm{A}+\mathrm{B}}\\ {\displaystyle }& {\displaystyle }+\sum _{j=\mathrm{1}}^W\left[\stackrel{\mathrm{̃}}{F}\left(p_j^{\mathrm{B}}\right)-\mathrm{1}\right]\sum _{i=\mathrm{1}}^W{p}_{ij}^{\mathrm{A}+\mathrm{B}},\text{or}\\ {\displaystyle }\sum _{i,j}^W\left[\stackrel{\mathrm{̃}}{F}\left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)-\mathrm{1}\right]& {\displaystyle }{p}_{ij}^{\mathrm{A}+\mathrm{B}}=\sum _i^W\left[\stackrel{\mathrm{̃}}{F}\left(p_i^{\mathrm{A}}\right)-\mathrm{1}\right]p_i^{\mathrm{A}}\\ \text{(31)}& {\displaystyle }& {\displaystyle }+\sum _j^W\left[\stackrel{\mathrm{̃}}{F}\left(p_j^{\mathrm{B}}\right)-\mathrm{1}\right]p_j^{\mathrm{B}}.\end{array}$$

(Note that the number of states allowed may be different for the two subsystems, W_A≠W_B, but here it does not make any difference to consider $W_A=W_B=W$.)

We recall that $\stackrel{\mathrm{̃}}{F}\left(x\right)\equiv \frac{\mathrm{1}}{-{\mathit{\lambda }}_{\mathrm{1}}}{f}^{\prime }\left(x\right)$; thus, we find

$$\begin{array}{ll}\text{(32)}& {\displaystyle }& {\displaystyle }\sum _{i,j}^W\left[{\displaystyle \frac{\mathrm{1}}{-{\mathit{\lambda }}_{\mathrm{1}}}}{f}^{\prime }\left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)-\mathrm{1}\right]p_{ij}^{\mathrm{A}+\mathrm{B}}={\displaystyle }& {\displaystyle }\sum _i^W\left[{\displaystyle \frac{\mathrm{1}}{-{\mathit{\lambda }}_{\mathrm{1}}}}{f}^{\prime }\left(p_i^{\mathrm{A}}\right)-\mathrm{1}\right]p_i^{\mathrm{A}}+\sum _j^W\left[{\displaystyle \frac{\mathrm{1}}{-{\mathit{\lambda }}_{\mathrm{1}}}}{f}^{\prime }\left(p_j^{\mathrm{B}}\right)-\mathrm{1}\right]p_j^{\mathrm{B}}.\end{array}$$

We compare this relationship with the additivity of entropy:

$$\begin{array}{ll}{\displaystyle }{S}^{\mathrm{A}+\mathrm{B}}& {\displaystyle }=\sum _{i,j}^{W}f\left(p_{ij}^{\mathrm{A}+\mathrm{B}}\right)=\sum _i^{W}f\left(p_i^{\mathrm{A}}\right)+\sum _j^{W}f\left(p_j^{\mathrm{B}}\right)\\ \text{(33)}& {\displaystyle }& {\displaystyle }=S^{\mathrm{A}}+S^{\mathrm{B}}.\end{array}$$

The two functions f(x) and $\left[\frac{\mathrm{1}}{-{\mathit{\lambda }}_{\mathrm{1}}}{f}^{\prime }\right(x)-\mathrm{1}]\cdot x$ have the same additivity property. Therefore, one function f that can ensure the additivity of entropy is the one that obeys conforms to the proportionality, $f\left(x\right)\propto \left[\frac{\mathrm{1}}{-{\mathit{\lambda }}_{\mathrm{1}}}{f}^{\prime }\right(x)-\mathrm{1}]\cdot x$, or the differential equation

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }f\left(x\right)=c\cdot \left[{\displaystyle \frac{\mathrm{1}}{-{\mathit{\lambda }}_{\mathrm{1}}}}{f}^{\prime }\left(x\right)-\mathrm{1}\right]\cdot x,\\ \text{(34)}& {\displaystyle }& {\displaystyle }\text{or}{f}^{\prime }\left(x\right)+{\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{1}}}{c}}{\displaystyle \frac{\mathrm{1}}{x}}f\left(x\right)=-{\mathit{\lambda }}_{\mathrm{1}},\end{array}$$

with solution

$$\begin{array}{}\text{(35)}& f\left(x\right)={\mathit{\lambda }}_{\mathrm{1}}\cdot {\displaystyle \frac{x-x^{\frac{-{\mathit{\lambda }}_{\mathrm{1}}}{c}}}{\frac{{-\mathit{\lambda }}_{\mathrm{1}}}{c}-\mathrm{1}}}+f\left(\mathrm{1}\right)\cdot x^{\frac{{-\mathit{\lambda }}_{\mathrm{1}}}{c}}.\end{array}$$

(Note that the selection of proportionality between the two functions f(x) and $\left[\frac{\mathrm{1}}{-{\mathit{\lambda }}_{\mathrm{1}}}{f}^{\prime }\right(x)-\mathrm{1}]\cdot x$ makes the derivation of Eq. (34) a sufficient but not necessary condition. Other functional forms may also exist, for example, a linear combination of the two functions mentioned.)

A fully organized system has zero entropy, so that $S(p_i=\mathrm{1},p_j=\mathrm{0}\forall j:\mathrm{1},\mathrm{\dots },W,\mathrm{with}j\ne i)=\mathrm{0}$. Then, from Eq. (10a) we find $S=\mathrm{0}=f\left(\mathrm{1}\right)+(W-\mathrm{1})f\left(\mathrm{0}\right)$. Equation (12) gives f(0)=0; hence, we find f(1)=0, too. Then, we set $q\equiv \frac{{-\mathit{\lambda }}_{\mathrm{1}}}{c}$, where we find

$$\begin{array}{}\text{(36)}& f\left(x\right)={\mathit{\lambda }}_{\mathrm{1}}\cdot {\displaystyle \frac{x-x^q}{q-\mathrm{1}}},\end{array}$$

or, setting also λ₁=1 (that is, setting the entropic unit k_B equal to 1), we end up with

$$\begin{array}{}\text{(37)}& f\left(x\right)={\displaystyle \frac{x-x^q}{q-\mathrm{1}}}.\end{array}$$

Therefore, the entropic function $S={\sum }_{k=\mathrm{1}}^{W}f\left(p_k\right)$ becomes

$$\begin{array}{}\text{(38)}& S={\displaystyle \frac{\mathrm{1}}{q-\mathrm{1}}}\cdot \sum _{k=\mathrm{1}}^W\left(p_k-p_k^q\right),\end{array}$$

that is, the Tsallis entropic formulation that builds the nonextensive statistical mechanics.

We note that Eq. (12) is invariant under linear transformations:

$$\begin{array}{ll}{\displaystyle }f\left(x\right)\to f\left(x\right)+a(x+b)\text{with}& {\displaystyle }a={\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{1}}-\mathrm{1}}{\mathrm{1}+(q-\mathrm{1})\frac{W-\mathrm{1}}{W-\mathrm{2}}}},\\ \text{(39)}& {\displaystyle }& {\displaystyle }b={\displaystyle \frac{\mathrm{1}}{W(W-\mathrm{2})}},\end{array}$$

which leads again to Eq. (15).

5 Conclusions

The paper resolved a basic problem about the origin of the distributions and statistical mechanics applied in space plasmas. Kappa distributions, or combinations/superposition thereof, can describe the velocities and energies of the plasma populations in space plasmas. While these empirical distributions have been used since the mid-1960s for modeling space plasma datasets, their statistical origin remained unknown. It was just about a decade ago that the connection of these distributions with the statistical framework of nonextensive statistical mechanics was completed and understood (Livadiotis, 2017a; chap. 1). Indeed, the kappa distribution is the outcome of the maximization of the q entropy of Tsallis under the constraints of a canonical ensemble (identifying the q exponential distributions, first used in a statistical framework context in Tsallis, 1988, as kappa distributions). Once this concept was understood by the science community, the next question was about the physical origin and reasoning of this entropic formula. This paper showed that the q entropy, which is the entropic formula that when maximized leads to the kappa distribution, can be derived under simple first principles and conditions, namely, by considering that energy and entropy are both additive physical quantities.