Fractal analysis of geomagnetic data to decipher pre-earthquake processes in the Andaman–Nicobar region, India

Seismo-electromagnetic (SEM) signatures recorded in geomagnetic data prior to an earthquake have the potential to reveal pre-earthquake processes in focal zones. The present study analyses the vertical component of geomagnetic field data from March 2019 to April 2020 using fractal and multifractal approaches to identify the EM signatures in Campbell Bay (CBY), a seismically active region of Andaman and Nicobar. The significant enhancements in monofractal dimension and spectrum width components of multifractal analysis arise due to superpositioned high- and low-frequency SEM field emitted by the pre-earthquake processes. It is observed that the higher-frequency components associated with microfracturing dominating signatures of earthquakes occurring around the West Andaman Fault (WAF) and Andaman Trench (AT), while the lower frequencies, which result from slower electrokinetic mechanisms, have some correlation with the earthquakes around the Seulimeum strand (SS). Thus, the monofractal, spectrum width, and Hölder exponent parameters reveal a different nature of pre-earthquake processes that can be identified, on average, 10, 12, and 20 d prior to the moderate earthquakes, which holds promise for short-term earthquake prediction.

1 Introduction

The existence of precursory signatures prior to an earthquake is a hotly debated topic among researchers across the globe. Convincing evidence of gas exhalations, variations in groundwater level, temperature variations, fluctuations in the electric and magnetic fields, etc. (Scholz et al., 1973; Rikitake, 1975; Crampin et al., 1980; Bella et al., 1995; Virk et al., 2001; Chadha et al., 2008; Koizumi et al., 2004; Liu et al., 2006; Ouzounov et al., 2007; Panda et al., 1996, 2007; Sethumadhav et al., 2010; Hayakawa and Molchanov, 2004) tilts the scale in favor of detectable signatures of pre-earthquake phenomena. Heterogeneous lithospheric material under strain undergoes microfracturing, which causes the polarization of charges that, in turn, leads to the generation of electromagnetic emission and acoustic–gravity waves (Molchanov and Hayakawa, 1995). It has been postulated that most crustal rocks contain dormant electronic charge carriers in the form of peroxy defects that are released under critical stress levels and flow out of the stressed sub-volume as an electric current, which generates magnetic field variations and low-frequency electromagnetic (EM) emissions (Freund and Sornette, 2007). When they reach the Earth's surface, they lead to the ionization of air at the ground–air interface (Hayakawa et al., 1996), leading to small disturbances in the local geomagnetic field. Observations of electromagnetic emissions prior to an earthquake in frequency ranges from direct current (DC) frequency, ultra low frequency (ULF), very low frequency, electromagnetic pulses, and very high frequency (Bulusu et al., 2023; Conti et al., 2021; Han et al., 2016; Hattori et al., 2013a; Hayakawa et al., 1999, 1996; Johnston et al., 1984) have been reported by many researchers. The presence of precursory signatures in the ULF range has been extensively studied for earthquakes of M≥7, such as Biak, Spitak, Loma Prieta, Guam, Chi-Chi, and Chiapas (Fraser-Smith et al., 1990; Hattori et al., 2004b; Hayakawa et al., 2000, 1999; Ida et al., 2008; Kopytenko et al., 1993; Molchanov et al., 1992; Smirnova et al., 2013; Stanica and Stănică, 2019; Yen et al., 2004); the earthquakes in the ULF range has received more attention as they experience less attenuation and are more likely to reach the Earth's surface and geomagnetic recording stations. Hayakawa et al. (2005) have examined the three-component data from the same station to identify the anomalous signatures in the polarization ratio of the ULF geomagnetic signal and the diurnal ratio of the Z component for these moderate earthquakes and found a correlatable pattern of these signatures with an earthquake occurrence in 75 % of the events. This encouraged a deeper investigation into the possible causes of these patterns.

Identification of the geomagnetic anomalies, which are associated with lithospheric processes, is a contentious issue. These variations, which are distinct from the expressions of magnetospheric–ionospheric processes due to interaction with the solar wind, must be uniquely identified. The preferred signal processing techniques in previous studies are polarization ratio analysis, diurnal ratio, principal component analysis, singular value decomposition, and monofractal and multifractal analyses (Bulusu et al., 2023; Gotoh et al., 2002; Hattori et al., 2004b; Hayakawa et al., 2007, 2005, 1999; Rawat et al., 2016). These signal processing techniques have shown promising results in different cases, such as central frequency of 0.01 Hz of non-overlapping window of nighttime data studied by Han et al. (2015), Hattori et al. (2013b), and Xu et al. (2013) using a filtered diurnal signal (using a Daubechies wavelet function, db5) of the target station and reference station; Han et al. (2015) studied the diurnal ratio of electric as well as magnetic fields along with the polarization ratio of the magnetic field of nighttime data in the ULF range, and Heavlin et al. (2022) studied the signal from a dense network of stations using linear discrimination analysis (LDA) in the frequency range of 0.001–25 Hz.

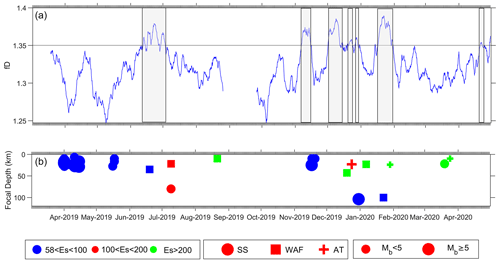
The Andaman–Nicobar region lies in the northern part of the Sumatra subduction zone, where the Indian plate is thrusting under the Burma microplate (Gahalaut et al., 2013; Meng et al., 2012; Yang et al., 2017). Persistent tectonic activity is observed here along three major faults, i.e., West Andaman Fault (WAF), Aceh strand (AS), and Seulimeum strand (SS). Some of the major earthquakes along these faults have led to huge losses of life and property and continue to be a worrisome source of mega-scale hazards. During March 2019 to April 2020, 63 moderate earthquakes of M≥4.5 occurred in the vicinity of the geomagnetic station installed by Council of Scientific and Industrial Research National Geophysical Research Institute (CSIR-NGRI) at Campbell Bay (CBY) in Great Nicobar (Fig. 1). The self-organized critically (SOC) property of earthquakes provides the motivation to study the fractal characteristics of the geomagnetic time series to decipher the nature of anomalous signatures in the data (Bak et al., 1988; Hayakawa et al., 1999).

The behavior of natural biological, physical, and geophysical parameters exhibits fractal and multifractal geometries. Mandelbrot (1980) introduced fractals to characterize the highly complex geometry such as shape of cloud, coastlines, and rough surfaces of mountains and landscapes, where traditional Euclidean geometry fails to characterize the nature of such complex geometries, whereas fractals facilitate description of complex geometries (Barnsley et al., 1989). In 1977, after the publication of Mandelbrot's book Fractals: From, Chance and Dimension, the concept of fractal geometries was considered a popular tool among researchers of remote sensing for the extraction of land surface features from high-resolution remote sensing data (Haralick et al., 1973; Weszka et al., 1976). Several applications of fractals are observed in image processing for decomposition and extraction of image texture (Pentland, 1984; Myint, 2003). Moreover, the urban system (population size and areas) also shows scaling and SOC nature, and the nature of its growth, economics, morphology, genesis, and planning is well characterized by the fractal approach (Keersmaecker et al., 2003; Chen and Zhou, 2008; Chen, 2010). Fractals have diverse applications in different fields of science, such as medical science (Lopes and Betrouni, 2009), material science (Schaefer, 1988), telecommunication (Werner et al., 1999), environmental science (Xu et al., 1993), and computer graphics (Jacquin, 1993). After gaining popularity in the space domain, applications of fractal methods to time domain data started in the 1980s in the fields of finance and economics to characterize rapidly evolving systems. The application of fractals is also observed in geophysical time series data in the characterization of a natural phenomenon such as the solar corona and space plasmas (El-Nabulsi and Anukool, 2024; Borovsky, 2021); frequency size distribution of earthquakes or temporal patterns of earthquake parameters such as the magnitude, energy, depth, and hypocenter (Hayat et al., 2019; Telesca et al., 2003; Rahimi-Majd et al., 2022); and modeling of geological features from geophysical data such as seismology, earthquake dynamics, and well logs (El-Nabulsi and Anukool, 2022; Leary, 1991; Dolan et al., 1988). In recent years, it has been noted that the natural lithospheric processes due to tectonic activity, such as heat flow on oceanic ridges (Cheng, 2016), mineralization due to hydrothermal processes (Wang et al., 2017), and earthquakes with different magnitudes (Turcotte, 1997), exhibit a fractal nature. From fractal theory, the changes in fractal dimension represent the dynamic evolution of the state of the system; the non-linear dynamics of an active tectonic plate can be modeled with fractal geometry (Dimri, 2005). The fractal method has become a popular tool in the characterization of the complexity of the dynamic evolution of several types of natural processes, including the complex behavior of seismicity. The fractal nature of the distribution of the hypocenter and seismicity pattern was first demonstrated by Kagan and Knopoff (1980) and Hirata and Imoto (1991). The spatial distribution of earthquakes shows fractal behavior, wherein the fractal dimension can give an idea of heterogeneities of geological compositions and the degree of the fracturing of rocks (Pastén and Pavez-Orrego, 2023). Fractal methods such as Hausdorff dimension, box counting, and correlation dimension are commonly used to study the complex nature of the Earth system and obtain deeper insights into seismicity and its relation to tectonic forces (Potirakis et al., 2017; Molchan and Kronrod, 2009; Chen et al., 2006; Mandal et al., 2005). The efficacy of applying fractal methods to study geomagnetic field patterns prior to earthquake occurrence was a later development (Hattori, 2004; Potirakis et al., 2017; Ida et al., 2012; Hayakawa et al., 2000). For example, in the case of the Guam earthquake 1993, a significant change in the scaling exponent prior to the event was found (Hayakawa et al., 1999). A similar behavior of the scaling exponent was also observed prior to the Biak earthquake in 1996 (Hayakawa et al., 2000).

After the several application of fractals in earthquake research, the researcher found that the earthquake processes and seismicity in time and space are comprised of more than one fractal property, i.e., multifractal instead of fractal. Multifractal methods have diverse applications in extracting the dynamic nature of earthquakes in both spatial and time domains. In the spatial domain, multifractal analysis is used to characterize the pattern of seismicity, stress distribution, clustering, or intermittency of spatial earthquake distribution (Godano et al., 1996; Roy and Mondal, 2012; López-Casado et al., 2014; Rossi, 1994). Multifractal analysis of the dynamic properties of earthquakes in the time domain reveals the temporal complexity of seismic activity. This insight into earthquake dynamics may aid in the forecasting future seismic events. For example, Kiyashchenko et al. (2003) studied the dynamics of seismicity distribution using multifractal parameters (the minimum of the Hölder exponent and the first-order Hölder exponent) and found a significant decrease prior to major earthquakes. Such characteristics can be used as earthquake precursory signatures. Similarly, Telesca et al. (2004) studied the geomagnetic field from two seismically active regions (Japan and California) and found temporal variations in multifractal parameters – namely, entropy and higher-order fractal dimensions – which may indicate processes associated with the preparation of large-magnitude earthquakes. Moreover, the generalized multifractal dimension at higher orders (q>1) of ULF geomagnetic field data showed a significant change prior to the 1993 Guam earthquake (Ida et al., 2005). Similarly, multifractal analysis of geomagnetic signals from volcanic eruptions revealed complex dynamics that decreased after eruptions (Currenti et al., 2005). Further, Telesca et al. (2003) analyzed geoelectrical signals recorded in seismically active regions using fractal and multifractal tools and concluded that the multifractal tools have greater potential for extracting seismo-electrical signatures associated with earthquakes. Smirnova et al. (2013) observed a notable decrease in the higher-order fractal dimension (derived from the generalized fractal dimension) of geomagnetic signals prior to the 1995 Kobe earthquake.

These natural non-linear processes give rise to a self-similar pattern and long-range correlations, which are mathematically described by power law relations. Box counting and the Hausdorff method are the two fundamental methods to determine the fractal dimension of geometries in the time or space domains. Box counting involves the counting of boxes (of fixed sizes) that contains at least one value of fractal objects (Liebovitch and Toth, 1989). This process is repeated with different box sizes; therefore, the size of the boxes and the number of boxes with at least one values relate to the fractal dimension of objects. The Hausdorff method is similar to box counting, except that the fractal object is measured by a different diameter, and the measured fractal values are called Hausdorff measures. The Hausdorff dimension is related to the Hausdorff measures and the variable diameters used for measuring the fractal objects. Fractal methods, such as detrended fluctuation analysis (DFA), scaling structure function, and Higuchi fractal dimension, are common methods for analyzing the geomagnetic signals. Moreover, multifractal geometries do not exhibit a self-similar pattern and hold different fractal dimensions. The spectra of fractal dimension values are determined from sets of fractals used to delineate the multifractal nature of objects, also known as the generalized fractal dimension (Mandelbrot, 1989). In multifractals, the frequency of the exponents or fractal dimension indicates the presence of the prominent fractal nature of geometries. The strength of fractals or their weight is measured by certain parameter q in the range of $\mathrm{0}>q>\mathrm{0}$. The multifractal methods wavelet transform modulus maxima (WTMM) or wavelet discrete wavelet transform (DWT), and multifractal detrended fluctuation analysis (MFDFA) are very common methods for the analysis of geomagnetic signals.

For our data, the fractal nature is tested with different approaches (Higuchi, 1988); the Higuchi method provides a more consistent and reliable fractal dimension value for the study of the fractal behavior of ULF signal (Hattori et al., 2004a; Gotoh et al., 2003; Smirnova et al., 2004). Further, multifractal techniques can better represent the different sources of the signals associated with seismicity (Turcotte, 1989). In this study, we will use the nighttime Z-component geomagnetic signal as it is more sensitive to changes in local EM emissions, which are likely to be generated by microfracturing processes associated with lithospheric deformation. We propose to compute the fractal and multifractal dimensions of the vertical component of geomagnetic data to extract SEM signatures from more intense perturbations of the signal represented by higher fractal dimension values. The anomalous EM emissions can be correlated with earthquake events in search of pre-earthquake signatures. The earthquake catalog (Table S1) of the study region is adopted from the International Seismological Centre (ISC) with M≥4.5 and the epicenter within a 250 km radius of the recording station. In total, 63 earthquakes were recorded from 31 March 2019 to 24 April 2020.

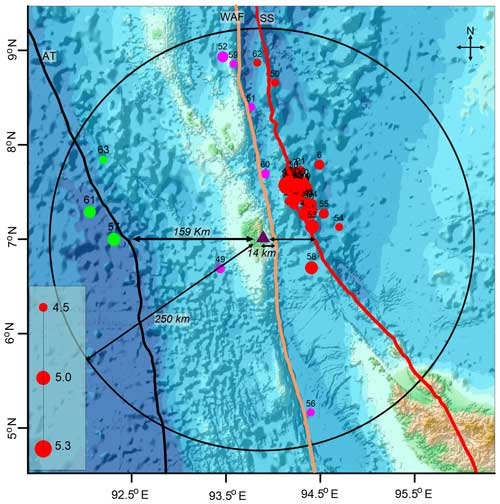
Figure 1 Bathymetry map of the Andaman–Nicobar subduction zone, including the Sumatran Fault System, i.e., Seulimeum Strand, West Andaman Fault, and Andaman Trench (modified after Cochran, 2010; Anusha et al., 2020). The circles representing the earthquake's location and magnitude (size of circle) correspond to each fault system.

2 Methodological approach

It is proposed to apply both fractal and multifractal approaches to the Z component of the geomagnetic field to distinguish between the different source characteristics and examine their relationship with earthquake parameters. The vertical component of the geomagnetic field is preferred for analysis because it is more sensitive to the local electromagnetic field, which is often generated by lithospheric deformation.

The fractal behavior of the Z component for 1 d data using the Higuchi method is tested and examined. Gotoh et al. (2003) tested different methods for the estimation of the fractal dimension of the geomagnetic signal and suggested that the fractal dimension value using the Higuchi method, provided in the equation below, is more reliable and consistent than others. In the Higuchi method, a time series, x(n), decomposed into time series of different length values, $x_k^m$, defined as $x_k^m:x\left(m\right),x\left(m+k\right),x\left(m+\mathrm{2}k\right),\mathrm{\dots }\cdot x\left(m+\left(\frac{N-k}{k}\right)\cdot k\right)$, where n is $\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{\dots },N$; m is 1, 2, 3, …, k; and k is 1, …, k_max. If the average lengths of decomposed time series L_m(k) computed at an interval of time from k=1 to k_max are related to each other as follows:

$$\begin{array}{}\text{(1)}& L\left(k\right)\propto k^{-f_{\mathrm{D}}}.\end{array}$$

From Eq. (1), f_D is equal to the slope of fitted line over log (L(k)) versus $\log \left(\frac{\mathrm{1}}{k}\right)$ and is considered the fractal dimension of time series data, x(n). The regression line over log (L(k)) versus $\log \left(\frac{\mathrm{1}}{k}\right)$ obtained from the Higuchi method (indicating power law behavior) of a 1 d nighttime (22:00–02:00 LT) Z component of the geomagnetic signal on 3 April 2019 is shown in Fig. 2.

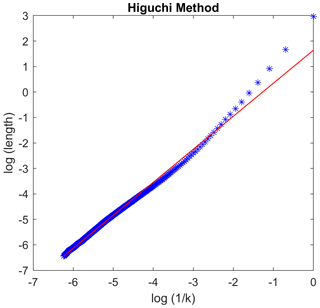
Figure 2 The linear fitting over the log of average length and log of size of time interval (scale), showing the power law nature of geomagnetic signal.

For multifractal analyses, the Haar wavelet function is used for the discrete wavelet transform because it decomposes the signal into high- and low-wavelet coefficients. The discrete wavelet transform decomposes the signal up to the maximum level defined by $\log \mathrm{2}\left(\text{length of}\right(X\left(t\right))/(\text{length}\left({\mathit{\psi }}_{\mathrm{0}}\right)+\mathrm{1}\left)\right)$.

The wavelet function, ψ₀, used to compute the wavelet coefficient of time series, X(t), using discrete wavelet transform (DWT) with a different level of decomposition at the dyadic scale (2^−j) is defined as follows:

$$\begin{array}{}\text{(2)}& w_x\left(j,k\right)=\int X\left(t\right){\mathrm{2}}^{-j}{\mathit{\psi }}_{\mathrm{0}}({\mathrm{2}}^{-j}t-k)\mathrm{d}t,\end{array}$$

where w_x(j,k) is the wavelet coefficients at scale j and time k. Further, the wavelet leader values at each level decomposition are defined using w_x(j,k).

The wavelet coefficients in the dyadic interval λ(jk) at the scale of 2^j is the union of two intervals at the scale of 2^j−1, and 3λ (jk) is the union of three, i.e., ${\mathit{\lambda }}_{j,k-\mathrm{1}}\cup {\mathit{\lambda }}_{j,k}\cup {\mathit{\lambda }}_{j,k+\mathrm{1}}$. Thus, the largest value of coefficients that occurred at the scale of 2^j from the union of dyadic scales is referred to as the wavelet leader, i.e., the following applies (Lashermes et al., 2005):

$$\begin{array}{}\text{(3)}& L_X\left(j,k\right)\equiv L_{\mathit{\lambda }}={\sup }_{{\mathit{\lambda }}^{\prime }\subset \mathrm{3}\mathit{\lambda }}\mathrm{|}{w}_x\left(\mathrm{d}{\mathit{\lambda }}^{\prime }\right)\mathrm{|},\end{array}$$

where L_X(j, k) is the wavelet leader at the scale of j and time k.

Since the time series X(t) holds the condition of regularity, the wavelet leaders follow the power law relation, and the associated scaling exponent of X(t) at t is h(t). The wavelet leaders selected from the maximum values of wavelet coefficients at each scale provide the supreme value of the scaling exponent, i.e., Hölder exponent. Thus, the Hölder exponent, h, and wavelet leaders at scale j and time k at limit of fine scales 2^j→0 are related as follows (Wendt, 2008):

$$\begin{array}{}\text{(4)}& L_X\left(j,k\right)\le C{\mathrm{2}}^{jh}.\end{array}$$

For the purpose of the generalization of Hölder exponent values, the structure function of the wavelet leader is estimated at each scale (2^j), with moment order q. The time average of (the qth power of) L_X(j, k) is referred to as the structure function (with n_j) at a scale (2^j), which is defined as

$$\begin{array}{}\text{(5)}& S^L\left(q,j\right)={\displaystyle \frac{\mathrm{1}}{n_j}}\sum _{k=\mathrm{1}}^{n_j}{\left|L_X\left(j,k\right)\right|}^q,\end{array}$$

where n_j is the number of wavelet leaders at scale j.

Since the time series function and wavelet leaders hold the regularity condition, the structure functions also follow power law behavior for 2^j→0 and can be defined as (Wendt et al., 2007)

$$\begin{array}{}\text{(6)}& S^L\left(q,j\right)=C_q{\mathrm{2}}^{j\mathit{\zeta }\left(q\right)}.\end{array}$$

From the above relation, the scaling exponent, ζ(q), is computed from the structure function using regression lines between log 2^j and S^L(q, j), which can alternatively be defined as

$$\begin{array}{}\text{(7)}& {\mathit{\zeta }}_L\left(q\right)=\sum _{j=j\mathrm{1}}^{\mathrm{2}}{w}_j{\log }_{\mathrm{2}}{S}^L\left(q,j\right),\end{array}$$

where w_j is weight factor.

Theoretically, the function for the multifractal spectrum of the scaling exponent, ζ_L(q), is based on the Legendre transform and defined as

$$\begin{array}{}\text{(8)}& f\left(h\right)\le \underset{q\ne \mathrm{0}}{min}\left(\mathrm{1}+qh-\mathit{\zeta }L\left(q\right)\right).\end{array}$$

In the present study, the equations from Wendt et al. (2007) are preferred for the computation of multifractal spectrum from L_X(j,k); i.e., the following applies:

$$\begin{array}{}\text{(9)}& {\displaystyle }f\left(q\right)=\sum _{j=\mathrm{1}}^{\mathrm{2}}{w}_j{U}^L\left(j,q\right),\text{(10)}& {\displaystyle }h\left(q\right)=\sum _{j=\mathrm{1}}^{\mathrm{2}}{w}_j{V}^L\left(j,q\right),\end{array}$$

where

$$\begin{array}{}\text{(11)}& U^L\left(j,q\right)=\sum _{k=\mathrm{1}}^{n_j}{R}_{X\left(t\right)}^q\left(j,k\right){\log }_{\mathrm{2}}{R}_{X\left(t\right)}^q\left(j,k\right)\end{array}$$

and

$$\begin{array}{}\text{(12)}& {\displaystyle }{V}^L\left(j,q\right)=\sum _{k=\mathrm{1}}^{n_j}{R}_{X\left(t\right)}^q\left(j,k\right){\log }_{\mathrm{2}}{L}_X\left(j,k\right),\text{(13)}& {\displaystyle }{R}_{X\left(t\right)}^q\left(j,k\right)={\displaystyle \frac{L_X{\left(j,k\right)}^q}{\sum L_X{\left(j,k\right)}^q}}.\end{array}$$

The larger width of the multifractal spectrum indicates larger multifractality or intermittency and vice versa. The width of the multifractal spectrum, h_w (from −q to +q), indicates the overall degree of the multifractality of the signal. The spectrum widths h_wp (q>0) and h_wn (q<0) indicate the weaker and stronger singularity of the multifractal signal. The h_max–h_min curve defines the average fluctuations embedded in the signal, while h(0) represents the zero-order exponent or monofractal dimension (Hayakawa et al., 1999). Similarly, f_max defines the exponent which occurred the maximum number of times. The application of multifractal using the Haar wavelet on 30 min nighttime (22:00–02:00 LT) data of the Z component of the geomagnetic signal on 3 April 2019 is shown in Fig. 3.

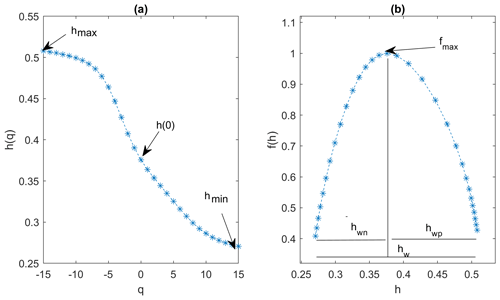
Figure 3 The multifractal analysis for 1800 samples of 3 April 2019. (a) The variation in the Hölder exponent (h) with moment order q in the range from −15 to +15, showing h_min, h_max, and h(0). (b) Multifractal spectrum showing the width of spectrums h_w, h_wp, and h_wn.

The following processes opted for the analysis of the geomagnetic time series signal in search of SEM signatures.

The high correlated values measured by fractal analysis are the reason to select the Higuchi method, while for the multifractal analysis, the wavelet leader is selected due to contact support for a wide range of values of q (−q to +q) and stability for the scaling function for negative q values compared to other techniques. From the fractal analysis the power law behavior and from multifractal analysis the finite width of the multifractal spectrum and variation in the Hölder exponent indicate the fractal and multifractal nature of the signal, respectively.

The fractal dimension, f_D, of the total duration of Z-component data is calculated for consecutive time windows of 30 min to trace the variations in the fractal dimension, producing eight values for each day. The choice of a 30 min time window (consisting of 1800 data points) is based on the balance between the stability of fluctuations in the fractal dimension and minimizing loss of information after trials with 15 min and 1 h time windows.

Similarly, the spectrum width parameters (h_w, h_wp, and h_wn) and Hölder exponent parameters (h_max, h_min, and h(0)) estimated for the total length of the Z component from window of 30 min to identify the degree of singularity or complexity (global, weaker, and stronger) as well as the degree of fluctuations with respect to amplitude (from smaller to larger). The shorter fluctuations in fractal dimensions are smoothed by applying a 15 d moving mean.

The increments in the fractal dimension and a multifractal parameter (spectrum width and Hölder exponent) value greater than the threshold value (μ+ σ) are considered a significant increment of evidence of the existence of EM signatures from the lithospheric deformation.

3 Results

3.1 Monofractal analysis

The temporal variations in f_D of the vertical component of the geomagnetic signal are shown in Fig. 4a; f_D values greater than the threshold value of 1.35 (defined by μ+σ) are indicated by grey rectangles. The increasing fractal dimension values are directly proportional to the increasing degree of complexity of the signal. A synthetic test of the fractal dimension on fraction Brownian motion signals (fBm) with Hurst exponents of 0.2, 0.4, and 0.5; i.e., a monofractal signal with an increasing degree of complexity (Fig. S1) shows higher fractal dimension values (from the Higuchi method; Fig. S2) for a lesser Hurst exponent signal. Moreover, the combination of all three signals, i.e., a multifractal signal, shows smaller fractal dimension values, indicating that multifractal signal cannot be characterized in detail using the monofractal dimension. Therefore, the observed enhancements in the f_D of the geomagnetic signal indicate a greater complexity in the signal resulting from the superposition of electromagnetic signals generated by an impending earthquake. These enhanced values possibly represent the additional complexity in the signal caused by pre-earthquake microfracturing. The temporal location of enhanced fractal dimension values and their correlations with forthcoming earthquakes are summarized in Table S2. For the earthquake swarm of 1–18 April 2019 and the three earthquakes on 16 and 17 May 2019, no preceding or coinciding enhancements are recorded. Two phases of enhancements during 12–13 and 16–19 June 2019 occur prior to the earthquake of 19 June 2019 (M=4.6, focal depth of 35 km, along the WAF, and with epicentral distance of 60 km). The enhancements during 20–26 June and 29 June–2 July 2019 occur before the dual earthquakes on 9 July 2019 (M=4.5, focal depth of 80 km, epicenter distance of 185 km, and along the SS fault and M=4.5, focal distance of 22 km, epicenter distance of 156 km, and along the WAF). No enhancements beyond threshold value are recorded prior to the very shallow 10 km depth earthquake on 21 August (M=4.8) with epicenter 219 km away along the WAF. During September and October 2019, neither earthquakes nor enhanced fractal dimensions are observed. Three earthquakes occurred in November, two on 17 November and one on 20 November, all on the SS fault. Their magnitudes were of M=5.1, 4.5, 4.7, respectively, at shallow focal depths, and they had corresponding epicenters at 60, 91, and 78 km from the recording site. These events are preceded by a long-duration enhancement in fractal dimension during 6–15 November. In December, three earthquakes occurred on 19, 24, and 30 December with magnitudes of 4.5, 5, and 5 on the WAF, AT, and SS faults, respectively. The earthquake on 19 December with a focal depth of 43 km, despite the large epicentral distance of 212 km from recording site, was preceded by a large amplitude and long-duration enhancement of the fractal dimension during 1–14 December; for the next two earthquakes of focal depths of 23 and 104 km and corresponding epicentral distances of 173 and 67 km, minor enhancements were observed during 18–23 December and 26–28 December. For the three earthquakes in January 2020, the M=4.5 shallow earthquake on 6 January with an epicentral distance of >200 km, no enhancements are observed. The earthquakes on 22 and 28 January occurred. No earthquakes were recorded in February 2020, and no anomalous enhancements are observed. On 19 and 24 March, there were two shallow earthquakes (M=4.5) with epicentral distances of more than 200 km along the SS and AT, respectively. During 20–22 April, a small enhancement is observed; the succeeding earthquake is not included in the present catalogue.

Figure 4 (a) Temporal variation in the fractal dimension estimated from the Higuchi method (15 d moving mean) of the Z component of the geomagnetic signal. (b) The timeline of earthquake occurrences for the same duration of the geomagnetic signal.

3.2 Multifractal analysis

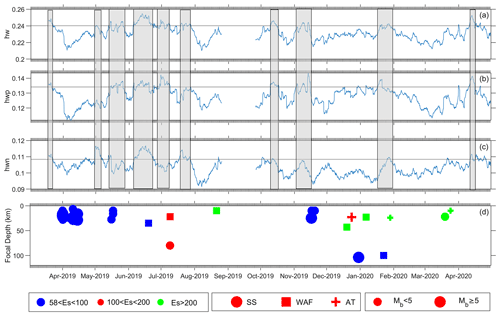
The Hölder exponent curve and multifractal spectrum width are calculated for the same data of 3 April 2019 for the 30 min interval of 22:00–22:30 LT with 1800 data points. The large variation in Hurst exponent against moment order q (Fig. 4a) and wide width of the multifractal spectrum of the geomagnetic time series (Fig. 4b) indicate the multifractal nature of the geomagnetic signal. The multifractal behavior of a signal is generally characterized by the width of the multifractal spectrum (h_w) as well as spectrum widths h_wn, corresponding to the range from −q to 0, and h_wp, corresponding to the range from +q to 0, also assist in characterizing the specific nature of the geomagnetic signal (Fig. 4). Apart from the spectrum width parameters, Hölder exponent parameters, such as h_min, h_max, h(0), and f_max are also useful in characterizing the nature of the pre-earthquake geomagnetic signal (Fig. 4).

3.2.1 Multifractal spectrum width

The width of the multifractal spectrum deciphers the nature of the complexity of analyzed signal; a higher spectrum width indicates a higher degree of heterogeneity. A synthetic test of the multifractal spectrum on fraction Brownian motion signals (fBm) with Hurst exponents of 0.2, 0.4, and 0.5 shows increasing width of the multifractal spectrum (Fig. S3). Moreover, the multifractal spectrum width of combined signal shows the highest values, indicating an increasing nature of complexity, which was not accurately determined by the monofractal dimension. The width of the multifractal spectrum (h_w, h_wp and h_wn) of a sliding window of 1800 data points (half an hour) without overlapping is computed for the whole time series of the vertical component of the Z component (Fig. 5). The 15 d moving mean of variation in spectrum width of multifractal spectrum shows significant variations in the range of 0.09 to 0.26. Enhancements that exceed the threshold value in any of the multifractal components (h_w, h_wp, and h_wn). This indicates a significant perturbation in the geomagnetic signal (Fig. 5). Enhancements that exceeded the threshold value in any of the multifractal components (h_w, h_wp, and h_wn) are classified as anomalies. For the earthquake swarm of 31 March–18 April 2019 (moderate magnitude of 4.5–5.3, shallow focal depth of 15–30 km, and epicentral distance of 50–100 km), a preceding enhancement (in h_w, h_wp, and h_wn) component occurred during 17–22 March 2019. The significant enhancement during 14 May (in h_w component), 14–15 May, 17–20 May (in h_wp component), and 29 April–5 May 2019 (in h_wn component) are partly common to each other and occurred prior to, alongside, and after earthquakes on 16 and 17 May 2019 (moderate magnitude of 4.5–4.8, focal depth of 10–27.4, and epicentral distance of 58–71). The two sets of enhancement during 22–25 May 2019 and 4–22 June 2019 (in h_w and h_wp) and one persistence enhancement during 8–22 June 2019 occurred prior to the earthquake on 19 June 2019 (M=4.6, focal depth of 60 km, and epicentral distance of 60 km). The enhancement in common duration 30 June–9 July 2019 (different duration of persistence), and no enhancement in the h_wn component occurred prior to two earthquakes on 9 July 2019 at two different locations with a moderate magnitude (4.5), moderate and shallow focal depth (80 and 22 km), and large epicentral distance (185 and 156 km). The common enhancement during 17–19 July 2019 in h_w and h_wn components (not the same duration of persistence) occurred prior to the earthquake on 21 August 2019 (M=4.8, focal depth of 10 km, and large epicentral distance of 219 km). The common enhancements during 9–15 October 2019 and 7–10 November 2019 in h_w and h_wp components, 11–12 November in the h_w component, and 2–3 and 12–14 November 2019 in the h_wp component occurred prior to the earthquakes on 17 and 20 November 2019 with a moderate magnitude (4.7–5.1), focal depth (10–25 km), and epicentral distance (60–91 km). Further, the four earthquakes that occurred during December 2019 and first week of January 2020 (moderate magnitude, moderate focal depth, and moderate to large epicentral distances) are not preceded by any significant enhancement in the components of the multifractal width parameter. The common enhancements during 16–20 January 2020 in h_w and h_wp components occurred prior to the earthquake on 22 January (M=4.6, focal depth of 100 km, and epicentral distance of 77 km) and 28 January 2020 (M=4.9, focal depth of 24 km, and epicentral distance of 204 km). Further, the two-earthquake events of May 2020 (moderate magnitude, shallow focal depth, and large epicentral distance) is not preceded by any enhancement in the components of the multifractal width parameter.

Figure 5 Temporal variation in spectrum widths h_w, h_wp, and h_wn are shown in panels (a), (b), and (c), respectively, and anomalous behavior is highlighted in grey. Panel (d) shows the occurrences of earthquake with magnitude (size of circle) and corresponding faults (different color).

3.2.2 Hölder exponent

The Hölder exponent parameters (h_max, h_min, h(0), and f_max) used for defining the multifractal spectrum curve also show significant variations in the amplitude; again, enhancements greater than the threshold value (1.0082, 0.4626, 0.5873, and 0.3612) are treated as significant (Fig. 6). The enhancements in h_max, h_min, h(0), and f_max components with corresponding earthquakes are summarized in Table S4.

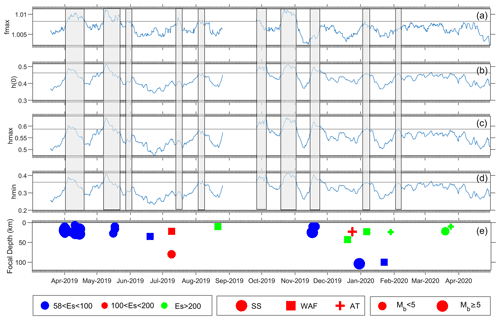
Figure 6 Temporal variation in Hölder exponent parameters, i.e., f_max, h(0), h_max, and h_min is shown in panels (a), (b), (c), and (d), respectively, and anomalous behavior is highlighted in grey. Panel (d) shows the occurrences of earthquakes with magnitudes (size of circles) and corresponding faults in different color.

The common enhancements during 2–18 April 2019 in all components of Hölder exponent coincide with the swarm of earthquakes from 31 March to 18 April 2019 with moderate magnitude, moderate focal depth, and moderate to large epicentral distance. The next common enhancements are noted during 6–14 May 2019 in all components of the Hölder exponent prior to the three earthquakes (moderate magnitude, focal depth, and epicentral distance), one on 16 May 2019, and two on 17 May 2019. For the same earthquakes, two small co- and post-seismic enhancements are noted in the f_max component during 17–19 May 2019. The small enhancement in only f_max during 20–21 May 2019 is preceded by the earthquake on 19 June 2019 with moderate magnitude, focal depth, and epicentral distances. Further, the two-earthquake event on 9 July with a moderate magnitude, large epicentral distance, and different location is not preceded by enhancements in any component of Hölder exponent. Two small enhancements during 15–16 July and 6 August 2019 in the f_max component and two small enhancements in h_min during 6 August 2019 occurred prior to the earthquake on 21 August 2019. The two enhancements common in all components but different durations, one small enhancement during 26 September–5 October 2019 and one persistent during 16 October–24 November 2019, occurred prior as well as coincident and post three earthquakes. Two of them were at a similar location on 17 November 2019, and one was at a different location on 20 November 2019 with a moderate magnitude, shallow to very shallow earthquake, and moderate epicentral distance. Further, three earthquakes that occurred in December 2019, the first two with a moderate magnitude and focal depth and large epicentral distance and the third with a moderate magnitude, large focal depth, and moderate epicentral distance, are not preceded by enhancement in any of the components of the Hölder exponent. The next small enhancement in the h_max component only during 3–8 January 2020 is coincident with earthquake on 6 January 2020 (moderate magnitude, moderate focal depth, and large epicentral distance) and preceded by two earthquakes on 22 and 28 January 2020 (with a moderate magnitude, moderate and large focal depth, and large and moderate epicentral distance).

For the earthquake swarm on 31 March 2019 and in early April, the spectrum width shows a small enhancement during 17–20 March, that is, 12 d prior to the earthquake cluster, which have magnitudes of between 4.5 and 5.3 and occur in a small region along the SS fault. There is no enhancement of the Hölder exponent. For the intermittent earthquakes in mid-April, there is no signal in the spectrum width, but the Hölder exponent shows a consistent enhancement during 3–10 April, a week before the main cluster. In early May, that is, up to 5 May, h_wn shows an enhancement; the pattern is mimicked in the Hölder exponent without crossing the threshold value. Small anomalous enhancements during 12–14 May in h_wn, h_wp, and h_w of spectrum width, just prior to the moderate earthquakes on 16 and 17 May. The Hölder exponent exhibits a longer, more consistent enhancement during 7–14 May, and f_max shows a co-seismic anomaly on 17–19 May followed by anomalies on 20–21 May. Post-seismic perturbations are also noted in spectrum width. For the M=4.6 earthquake on 19 June, long-duration anomalies are seen in spectrum width but not in the Hölder exponent. For the two earthquakes on 9 July, pre- and post-seismic anomalies are seen in spectrum width; only one anomaly is seen in the Hölder exponent during 14–16 June. There is no significant multifractal anomaly for the very shallow earthquake on 21 August. In October 2019, significant repeated anomalies are observed in the Hölder exponent right until November 2019. In the second half of January and much of February, there are several individual earthquakes; no significant enhancement is observed for any of them. A short enhancement can be noted during 11–14 April, which would be indicative of a future event.

3.3 Combined results of monofractal and multifractal analyses

Figures 4, 5, and 6 show that all the components from monofractal and multifractal analyses have different responses for each earthquake, indicating different characteristics of the signal, which can be used as indicator of pre-earthquake processes in the focal zone of the earthquake. In this regard, we have characterized the enhancements of components in three types of patterns: (i) present in only the monofractal component, (ii) present in only multifractal components, and (iii) present in the monofractal as well as in the multifractal component. The significant enhancement from both parameters (monofractal and multifractal) with the corresponding earthquake from Figs. 4, 5, and 6 is summarized in Fig. 7.

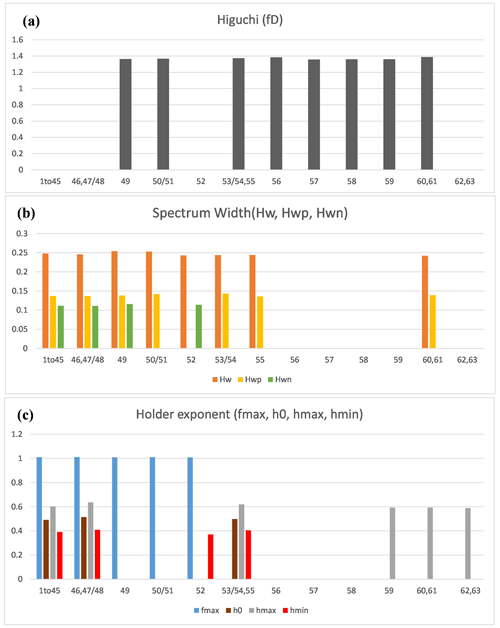
Figure 7 The components of significant enhancement with corresponding earthquakes from the (a) Higuchi fractal dimension, (b) spectrum width, and (c) Hölder exponent.

From Fig. 7 it is evident that the Higuchi fractal dimension from the monofractal analysis exhibits significant enhancements corresponding to earthquakes 56, 57, and 58, while there are no enhancements in the multifractal component that correspond to same earthquake. Furthermore, there are significant enhancements in multifractal components that correspond to earthquakes 1–45 (swarm of earthquakes), 46, 47/48, 52, 62, and 63, while there are no enhancements in the monofractal component (or Higuchi fractal dimension). It is also noted that the earthquakes 1–45, 46, and 47/48 exhibit all components of spectrum width (h_wn, h_wp, and h_w) and Hölder exponents (f_max, h_max, h_min, and h(0)), while for earthquakes 52 (h_w, h_wn, h_min, and f_max), 62 (h_max), and 63 (h_max), all components of multifractal parameters are not present. Similarly, the significant enhancements correspond to earthquakes 49, 50/51, 53/54, 55, 59, 60, and 61 observed in monofractal as well as multifractal components but not in all multifractal components. From multifractal parameters, it is also noted that the h_w component of spectrum width is present in each enhancement, the h_max component is present with each except for earthquakes 49, 50/51, and 52. Similarly, enhancements in f_max along with spectrum width, h_w, are present for all the earthquakes except 53/54, 55, 60, and 61. Significant enhancements for days where the Kp index is greater than 3 and Dst index smaller than −50 have been identified and removed from the study, although such short-duration effects considerably diminish after averaging each component with the 15 d moving mean (Fig. 8). An additional component of the diurnal ratio is also appended for correlation with monofractal and multifractal components, which is also treated with criteria of the planetary index (Fig. 8).

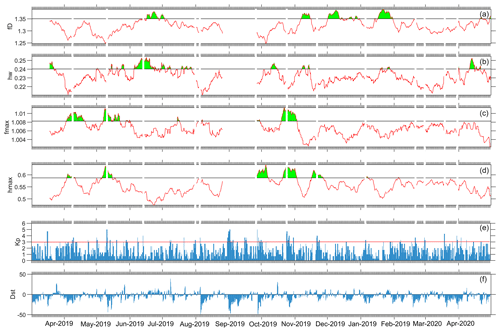
Figure 8 Temporal variation in the (a) Higuchi fractal dimension, (b) spectrum width component of multifractal parameter, (c) f_max component, (d) h_max component after removing the data correspond to (e) Kp > 3 and (f) Dst < −50.

Therefore, from the multifractal analysis, h_w, h_max, and f_max components and the Higuchi fractal dimension from the monofractal parameter have traced all the significant signatures corresponding to the seismogenic activity in the earthquake. The duration of the enhancement’s persistence is more clearly illustrated in the individual monthly figures presented in Figs S4-S17. From the total duration of the analysis, we have selected two quiet days, 25 May and 3 August 2019, and shown the geomagnetic field variation on corresponding date (Fig. S18), in which the first shows quite disturbed signatures (also showing high multifractal values) compared to the second (showing smaller multifractal values). This suggests that the disturbance in the geomagnetic field on the quiet day of 25 May 2019 is highly possible due to the interference of EM fields.

4 Discussion

We analyze the combined observations of the monofractal or Higuchi fractal dimension (f_D), alongside multifractal components (h_w, h_max, and f_max), in conjunction with the diurnal ratio. This comprehensive examination aims to uncover a connected pattern that may be associated with earthquake processes (Fig. 9). A swarm of earthquakes (1–45 as per our catalogue) along the SS fault occurred around the first week of April 2019. The data are available from 15 March, and no anomalies were identified in the diurnal ratio; hence, it was concluded that the data length was insufficient (Prajapati and Arora, 2023). While no anomalies were detected in the f_D, distinct enhancements are noted in spectrum width 14 d prior to the beginning of the swarm. Co-seismic f_max over the entire duration and muted h_max enhancements are noted during 2–18 and 2–10 April, respectively.

For the moderate-magnitude, shallow-focus earthquakes 46, 47, and 48, clustered close together during mid-June 2019, the diurnal ratio shows a significant enhancement 50 d before the events, whereas no anomalies are recorded in f_D. Enhancements in both h_max and f_max start 11 and 9 d before the events and continue co-seismically.

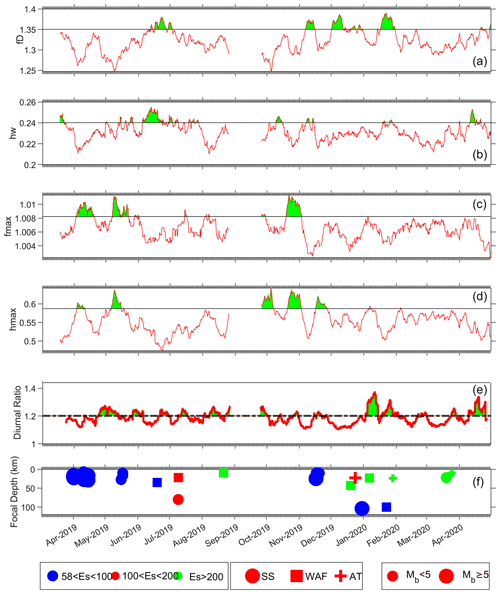
Figure 9 The significant enhancement in temporal variation in the (a) Higuchi fractal dimension; (b) spectrum width component of multifractal width parameter; (c) f_max component showing the Hölder exponent presence highest number of time; (d) h_max component showing the largest value of Hölder exponent; and (e) diurnal ratio, indicated by green shading. (f) The occurrences of earthquakes in same time duration with magnitude and focal depth.

Earthquake 49 on 19 June 2019 was of a moderate magnitude, moderate focal depth, and moderate epicentral distance on the WAF. It is preceded by a small enhancement in the diurnal ratio 22 d before and the f_D 7 d prior and continues co-seismically. The spectrum width enhancement starts 15 d prior to the event, which continues co-seismically, and there are no signatures in h_max or f_max.

Dual earthquakes 50 and 51 occurred soon after earthquake 49 at large epicentral distances on the WAF (shallow focal depth) and on the SS (deep focal depth) in the directions opposite to the recording station. Diurnal ratio shows a significant anomaly 16 d prior to the event, accompanied by a slight increase in f_D 19 d before. Mild perturbations are also observed in spectrum width 4–9 d before the events.

Earthquake 52 is similar to earthquake 49, with shallower focal depth and very large epicentral distance of 219 km on the WAF. It is preceded by the enhancement in the diurnal ratio seen 14 d before, and no signatures are seen in any other parameter.

Earthquakes 53, 54, and 55 on 17 and 20 November 2019 occurred along the SS fault with moderate epicentral distances and at shallow focal depth; earthquake 53 had a magnitude of 5. They are preceded by two phases of small enhancements in the diurnal ratio 21 and 3 d before the earthquakes, continuing to become co-seismic signatures. Enhancements in h_max continued and eventually became co-seismic signatures. Signatures in h_w are very muted, and f_D shows significant enhancement 2 d prior to the earthquakes.

Earthquakes 56–63 are individual events, from the end of 2019 to the first quarter of 2020, separated by intervals of several days to weeks in between. Earthquake 56 has very large epicentral distance, also occurring on the WAF like earthquake 52, but with a focal depth of 43 km. This is followed by earthquake 57, which is an M=5 earthquake at a very shallow focal depth at large epicentral distance on the AT. Earthquake 58 occurred on 30 December 2019 and was an M=5 event on the SS fault with a large focal depth and moderate epicentral distance. The events are preceded by a significant enhancement in f_D but had no other signatures. With only one station, it is not possible to construct an earthquake–anomaly link for this scenario. The cluster 53–54–55, for which signatures are noted in the diurnal ratio, f_D, and h_max, occurred in a closer duration period on the same SS fault at moderate epicentral distances and are also at shallow focal depths. Earthquake 59 is of a moderate magnitude and shallow focal depth but large epicentral distance on the WAF. Curiously, co- and post-seismic enhancements in the diurnal ratio are the sole signature for this event. For earthquakes 60 (large focal depth and moderate epicentral distance on the WAF) and 61 (shallow focal depth and large epicentral distance on the AT), the co-seismic enhancement in the diurnal ratio is accompanied by a similar enhancement in f_D. For earthquakes 62 (moderate magnitude, shallow focal depth, and large epicentral distance on the AT) and 63 (moderate magnitude, shallow focal depth, and large epicentral distance also on the AT), no preceding signatures are observed in any of the parameters. However, a distinct post-seismic increase in the diurnal ratio is noted.

In April 2020, enhancements in h_w during 10–14 April and the diurnal ratio during 10–24 April are observed.

Several research articles are available (Hayakawa et al., 1999; Gotoh et al., 2003; Ida et al., 2012) which study the behavior of the geomagnetic signal using non-linear signal processing techniques such as monofractal and multifractal in the context of EM fields generated from local sources due to seismogenic activity. Hayakawa et al. (1999) conducted analysis on the H, D, and Z components of a ULF geomagnetic signal recorded 65 km from the epicenter of the Guam earthquake (M=8) that occurred on 8 October 1993 at a focal depth of around 60 km using fractal (spectral method) and Hurst exponent analysis (rescaled range method, R/S). They inferred a decreasing value of slope (β) from 2.5 to ∼ 1 before the earthquake, which can be considered an indicator of SOC, where β ∼ 1.1 is critical value prior to the earthquake. However, no significant changes were observed in Hurst exponent by R/S analysis. The large-scale variation and a decrease in the ULF spectrum slope (or increase in fractal dimension) means an increase high-frequency fluctuations and is a proxy measure of a small-scale fractal structure caused by an active microfracturing process followed by the generation of seismogenic ULF emissions. In our study, we have also noticed the increase in the fractal dimension at least 10 d prior to the earthquake (for earthquakes 49, 50–51, 53–55, and 60–61) with a moderate magnitude (4.5<M<5.1); shallow and moderate focal depth (35, 51,14, and 62 km); and small, moderate, and large epicentral distances (60, 170, 76, and 140 km). The increasing fractal dimension before the earthquakes suggests the microfracturing processes in the Earth's crust to be the cause of the generation and emission of EM fields in the vicinity of the recording station.

Gotoh et al. (2003) analyzed the ULF geomagnetic data recorded at three stations on Izu Peninsula, Japan, where a nearby strong earthquake swarm lasted from 26 June to August 2000 with a magnitude of up to 6.5. A volcanic eruption happened simultaneously on Miyakejima. The Izu region on the Philippine plate is under tensile stress and seismically very active because of the subduction of the Pacific plate at Nankai and Sagami troughs (Uyeda et al., 2002). The monofractal dimension of the H component shows an increase a week before the earthquake. In the present study, we have analyzed the Z component instead of the H component because recent studies have suggested that the Z component is more sensitive for EM fields generated from local sources. In our study, we did not find any significant signatures of the enhanced fractal dimension of the Z component 1 week prior to a swarm of 45 earthquakes from 31 March to 18 April 2019; however, there is an enhancement in the spectrum width parameter (h_w) 10 d before the swarm activity started.

Further, Ida et al. (2005) carried out the multifractal analysis on the H component of the geomagnetic signal recorded 65 km from the epicenter of the Guam earthquake that occurred on 8 October 1993 at a focal depth of around 60 km. A westward movement of the Pacific plate and its subduction under the Philippine plate triggered the Guam earthquake (M_s=8.0) in a shallow dipping subduction zone with a strike-slip fault along the trench (Swan and Harris, 1993). Ida et al. (2005) found significant changes in the multifractal parameters of the Hölder exponent and spectrum width (α_min, α_max, w, Δ, f_max, α (f_max), and D_q for q<0, q>0, and q=0). The observation of the 9 d running means of spectrum width, w and α_max, shows clear and significant variation 30 d prior to the earthquake. In our analysis of multifractal parameters from earthquakes in the moderate subduction zone with a focal depth in the range of 10–30 km, the 15 d running means of spectrum width and the Hölder exponent show significant enhancements 12 and 20 d prior to those earthquakes which occurred close in time to a cluster (1–45, 47–48, 50–51, and 53–55). This difference in pattern may be due to the large differences in magnitude of the studied earthquakes.

Ida et al. (2012) analyzed the fractal dimension (estimated by the Higuchi method) of ULF data recorded at Kashi station, China, for approximately 4 years (March 2003 to December 2006), in which several moderate earthquakes occurred (greater than 5.0 and close to 6) at epicentral distances of 100 to 125 km, including one earthquake at approximately 300 km. The region is seismically very active due to the relative movement of plates along the SAF fault (normal fault) that is locally dominant in the area (He et al., 2015). Ida et al. (2012) applied the criterion of μ±2σ to define the significant variations in the fractal dimension and reported a decrease in the Z component for two earthquakes (M=5.7 and M=5.4), while the other earthquakes with magnitudes greater than 5 did not show any signatures. The enhancement in f_D is interpreted as an indication of the dominance of the high-frequency component and decrease in f_D as dominance of the low-frequency component, which may correlate with the high-frequency mechanism like microfracturing and slow processes like the electrokinetic effect, respectively. Potirakis et al. (2017) has analyzed geomagnetic data (H, D, and Z) at Kakioka station (KAK) at an epicentral distance of 300 km from the Tohoku earthquake (M 9.0) of 11 March 2011. The earthquake was caused by the rupture of a stretch of the subduction zone associated with the Japan Trench, which separates the Eurasian plate from the subducting Pacific plate. The data analyzed using DFA and the Higuchi method observed a significant decrease in the spectral exponent (using DFA) and corresponding increase in the fractal dimension (using the Higuchi method) 5–6 months prior to the large-magnitude Tohoku earthquake. In our study, we have found significant enhancements with the criterion of μ+σ, producing pre-seismic increases in f_D for multiple earthquake occurrences (50–51 and 53–55) with 4.6<M=5 and either shallow focal depth or small epicentral distance 19 and 11 d before the earthquakes. The concept of self-similarity in time series data was introduced by Mandelbrot and Van Ness (1968) and has been used to investigate patterns of seismicity to improve their predictability as early as the 1990s; for example, Godano and Caruso (1995) showed that multifractal characteristics of seismic catalogues are more appropriate, indicating varying degrees of clustering of seismic events. Fractal analysis has been used to study the fractal characteristics of geomagnetic field data to reveal the complexity and irregularity of the geomagnetic field and how they change in response to different conditions. For example, the analysis of the fractal properties of the geomagnetic field during different activity levels showed that the geomagnetic field is more multifractal during quiet periods than during storms and that the scaling properties of the field show long-term persistence (Babu and Unnikrishnan, 2023). Another study used the Higuchi method to calculate the fractal dimension of the geomagnetic field at a Russian magnetic station and found correlations between the fractal dimension and solar wind characteristics and the auroral electrojet (AE) index (Gvozdarev and Parovik, 2023) for studying geomagnetic secular variations (Sridharan and Ramasamy, 2006). Over the last 20 years, many researchers have examined the fractal characteristics of continuous geomagnetic field data in an earthquake zone to look for indications of anomalous changes in fractal dimensions, which may indicate the effect of the occurrence of an earthquake. So far, the results have shown promise but have not yet yielded definitive correlations, a clear argument that many more and systematic studies are required.

Fractal analysis of geomagnetic signals has revealed varying patterns and amplitudes of fractal dimensions representing seismo-electromagnetic (SEM) signatures. The amplitude of enhanced fractal dimension observed by Hayakawa et al. (1999) for an earthquake with a magnitude of 8 is approximately 10 times higher than the fractal dimension observed in our study (for earthquakes of a magnitude of 4.5–5.1). While enhancements from both studies are linked to microfracturing processes, the variation in amplitude creates ambiguity in connecting parameters such as the physical properties of the medium (conductivity, permeability, elastic modulus, etc.), scale of microfracturing, earthquake characteristics (epicentral distance, magnitude, and focal depth), and method used for computing fractal dimension. Gotoh et al. (2003) observed high fractal dimension values from the H component (in the noon sector, i.e., 12:00–13:00 LT) to be signatures of an earthquake swarm, whereas, in our study, we found signatures in multifractal parameters of the Z component (night sector, i.e., 22:00–02:00 LT. Thus, the fractal dimension shows different results depending on the data component (H or Z) and time of day (day or night) when characterizing similar earthquake events. Ida et al. (2012) observed a decrease in the fractal dimension of the Z component as a seismic precursor to major earthquakes. This observation contrasts with findings from the 2003 Guam and 2000 Izu Island earthquake swarms as well as our studies, which noted an increase in the fractal dimension before earthquakes. Ida et al. (2012) suggested that this discrepancy might stem from different dominant processes: inland pre-earthquake activity could be characterized by low-frequency electrokinetic processes, while oceanic activity might be dominated by high-frequency microfracturing processes. It should also be kept in mind that in the tropical regions, any diurnal variation in the atmospheric electrical potential will be more effective in changing the electrical current flowing to the Earth's subsurface compared with higher latitudes. Consequently, tectonic faults here can experience greater electrical currents as increased porosity and microfractures make them good conductors. These effects are likely to have a much stronger effect on the Z component of the geomagnetic field at lower latitudes. Moreover, earthquake catalogs for moderate-magnitude events may offer less precise parameters, such as magnitude, hypocenter, and focal depth. This imprecision can lead to the misinterpretation of fractal dimension results in the context of seismo-electromagnetic (SEM) signatures. Thus, interpretations of fractal variations in geomagnetic field data need to be made in the context of earthquake magnitudes and focal depths, focal mechanisms and triggering phenomena, location of the active faults, the distance of the geomagnetic recording station, and length of data available, as well as associated EM signatures like total electron content (TEC) changes and radon emissions in a systematic manner, which demand further in-depth study to resolve the ambiguities.

We have defined four clusters of the earthquakes under study (1–45, 47–48, 50–51, and 53–55). There are 10 earthquakes which occurred as single events. For the single events 52 and 56–63 (4.5<M<5.0), which are characterized by either a large focal depth (>100 km) or large epicentral distance (∼ 200 km), signatures are found in multifractal parameters. We infer that the EM fields from earthquakes with such a moderate magnitude and large epicentral distance are too weak to detect by multifractal and diurnal ratio approaches (Prajapati and Arora, 2023). For the same single events (with focal depth >100 km or epicentral distance ∼ 200 km), we observed that enhancements in f_D correspond to earthquakes 56, 57, 58, 60, and 61, while earthquakes 52, 59, 62, and 63 do not correspond to any pre-, co-, or post-seismic enhancements in the f_D parameter. The significant enhancement corresponds to five events out of nine, including two co-seismic signatures (60 and 61) that indicate the greater efficacy of the f_D parameter than the multifractal parameter for single events with a focal depth >100 km or epicentral distance ∼ 200 km. Earthquake 52 is associated with an increase in the diurnal ratio 13 d in advance. The single event, earthquake 49, is characterized by a moderate focal depth and epicentral distance, which is associated with co-seismic enhancements in f_D and pre-seismic signatures in h_w (7 d prior) and diurnal ratio (15 d prior).

The clusters, on the other hand, produce prominent signatures in the multifractal parameters. The first cluster (1–45) has a signature in h_w (14 d prior) and a co-seismic enhancement in f_max. The second cluster (47–48) has signatures in f_max, h_max, and diurnal ratio 9, 9, and 13 d prior to the event, respectively. The third cluster (50–51) at a larger epicentral distance of 165 km has signatures in f_D, h_w, and diurnal ratio 19, 9, and 19 d prior to the event, respectively. The fourth cluster (53–55) includes earthquakes of M=5.1, and the events are at a shallow focal depth and small to moderate epicentral distances and produce signatures in f_D and all the multifractal parameters as well as the diurnal ratio.

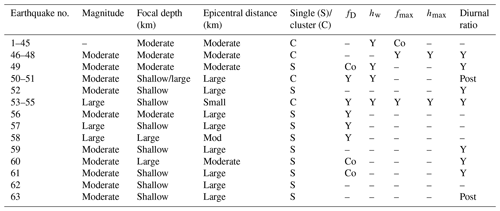
The combined observation from the fractals (mono- and multifractal) and diurnal ratio (Table 1) clearly indicates that the fractal parameters exhibit a significant enhancement associated with 10 earthquakes (including co-seismic signatures), while significant enhancements in diurnal ratio are correlated with 9 earthquakes out of 10 (including two post-seismic signatures).

Table 1 The following table summarizes the earthquake and its characteristic presence (Y) or absence (–) of potential enhancements in monofractal (f_D) and multifractal (h_w, f_max, h_max) components and diurnal ratio. Co and Post stand for enchantments in mono- and multifractal parameters simultaneously and after the occurrence of earthquake, respectively.

According to Ida et al. (2012), significant enhancements in fractal values of the geomagnetic signal recorded in tectonically active areas represent the dominance of the high-frequency component associated with EM fields from microfracturing processes in the lithosphere. Apart from this, the components of the Hölder exponent (part of multifractal analysis) such as f_max, h_max, h_min, and h(0) also analyze the different characteristics of the signal (Krzyszczak et al., 2019), such as an enhancement in h_max, which indicates that underlying processes of events are smoother, rather than short-duration fluctuations, while h_min is just opposite to h_max. Similarly, f_max corresponds to h; i.e., h occurred the maximum number of times in the range of h_max–h_min. The enhancements in the f_max value with a large h indicate the underlying processes are less correlated and have a fine structure; i.e., the signal is embedded with anomalies and not completely regular, while f_max corresponds to a smaller value of h, indicating the highly correlated and most stable signal. Enhancements in h_max and f_max with h correspond to a large h of a geomagnetic signal recorded in a tectonically active area, indicating that the underlying process is smooth and exhibits anomalies (less correlated and fine structures) of low frequencies. According to Conti et al. (2021), the electrokinetic process is responsible for the generation of a low-frequency EM signature from the lithospheric deformation of a focal zone.

The enhancements in h_max and f_max preceding the clusters of shallow earthquakes 1–45, 46–48, and 53–55 on the SS fault at moderate epicentral distances are indicative of low-frequency perturbations from multiple sources, which are ascribed to electrokinetic processes (Conti et al., 2021). For the cluster 50–51, the former occurs on the SS fault and the latter on the WAF, leading to interferences of the EM signals, whereby h_max and f_max enhancements are not prominent.

Earthquakes 49, 51, and 52 on the WAF dominated by strike-slip mechanisms are also shallow and are at moderate epicentral distances but have enhancements in f_D and h_w, with the latter being more significant. This is interpreted as high-frequency perturbations attributed to microfracturing processes (Ida et al., 2012).

The earthquakes 56, 57, 59, 60, 61, and 63 on the WAF and AT faults at large epicentral distances are linked with enhancements in f_D and h_w, with the former being more significant. We interpret these high-frequency perturbations to also be generated due to microfracturing processes; the large epicentral distances possibly leading to the attenuation of the highest-frequency components lead to more prominent monofractal signatures. Earthquakes 50, 58, and 62 are at either very large epicentral distances or large focal depths and fail to produce signatures in any of the fractal components.

The SEM signatures associated with earthquakes that have moderate focal depths and epicentral distances on the WAF fault are more pronounced in the h_w component. In contrast, the SEM signatures from earthquakes with large focal depths and epicentral distances on the WAF and AT faults are more prominent in the f_D component. This difference can be attributed to the greater attenuation of the SEM field that occurs with larger focal depths and epicentral distances, which often results in a less heterogeneous signal, thus favoring the f_D component. Conversely, the moderate or small focal depths and epicentral distances attributed to the lesser attenuation of SEM field causes more heterogeneous field, leading to a dominance in the h_w component. This means that the f_D component is the most sensitive component for earthquakes with a large epicenter and focal depth, while the h_w component is more sensitive for earthquakes with a moderate epicenter distance and focal depth.

5 Conclusions

The study of the fractal nature of the geomagnetic time series (Z component) allows us to conclude the following:

• The earthquake clusters that occurred on normal/thrust fault of moderate magnitude and focal depth are emitting prior EM fields of low frequency, effectively generated from electrokinetic processes in the focal zone of earthquake.

• The single earthquakes occurred on the strike-slip WAF fault of moderate magnitude and focal depth are emitting prior EM fields of more heterogeneity and frequency, while earthquakes on the same fault with a large epicenter distance/focal depth emitting prior EM fields of lesser heterogeneity and high frequency were effectively generated from microfracturing processes in the focal zone of the earthquake.

• The monofractal dimension, f_D, is more effective in tracing the EM fields from a large epicenter distance and focal depth, while multifractal spectrum width, h_w, is more effective in tracing the EM fields from a moderate to small epicenter distance and focal depth for the case of microfracturing processes.

• The fractal analysis has advantage over the diurnal ratio; it is a simultaneous observation of high- and low-frequency EM fields from the lithospheric deformation of the focal zone of the earthquake, which are emitted from different pre-earthquake processes.