the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Modelling of the terrain effect in magnetotelluric data from the Garhwal Himalaya region
Suman Saini
Deepak Kumar Tyagi
Sushil Kumar
Rajeev Sehrawat
The magnetotelluric (MT) method is a passive geophysical technique based on using time variations in the geoelectric and geomagnetic field to measure the electrical resistivity of the surface layer. It is one of the most effective geophysical techniques to study the deep structure of the Earth's crust, particularly in steep terrain like the Garhwal Himalaya region. MT responses are distorted as a result of undulating/rugged terrain. Such responses, if not corrected, can lead to the misinterpretation of MT data with respect to geoelectrical structures. In this study, two different correction procedures were used to compute the topography distortion for a synthetic model of the Garhwal Himalaya region from the Roorkee to the Gangotri section. A finite-difference algorithm was used to compute the MT responses (apparent resistivity and phase) for irregular terrain. The accuracy of the terrain correction procedures was checked using the results of different topography models for various periods from the literature. The relative errors between two terrain correction procedures were calculated with respect to the flat earth surface and were almost equal to zero for most of the sites along the Roorkee–Gangotri profile except at the foothill, where the error was high for shorter periods. The similar topography procedures of two terrain-corrected responses (TCR1 and TCR2) showed that there is no need for topography correction along the Roorkee–Gangotri profile because the slope angle is less than 1°.
- Article
(3879 KB) - Full-text XML
- BibTeX
- EndNote
Magnetotelluric (MT) methods were first explored by Tikhonov (1950) and Cagniard (1953) and were used to analyse the time-varying measured components of Earth's natural time-varying electric and magnetic fields to determine the shallow layers of the Earth. MT techniques have been successfully employed to explore a variety of Earth's resources, including oil, gas, minerals, and geothermal energy (Zhang et al., 2014; Patro, 2017; Mohan et al., 2017). These methods are effective for analysing deep crystal structures in challenging undulating terrains, such as the Himalayan region, compared with seismic methods (Tyagi, 2007; Israil et al., 2008, 2016; Kumar et al., 2014; Patro and Harinarayana, 2009; Kumar et al., 2018, 2022; Xiong et al., 2020; Kumar et al., 2021; Konda et al., 2023). Topography affects both the electric field and magnetic field components due to undulating topographical features, like hills and valleys, that distort the current lines (Wannamaker et al., 1986; Chouteau and Bouchard, 1988; Changhong, 2018; Kumar et al., 2018, 2022; Coggon, 1971). Therefore, the MT response functions of impedance and apparent resistivity become distorted when the MT sites are on or near the top of a hill or close to a valley.
Analytical and numerical techniques have been used to measure the topography distortion effect from MT data. Analytical techniques based on conformal mapping were used by Thayer (1975) and Harinarayana and Sarma (1982). Two-dimensional (2D) numerical techniques have been used for different types of terrain geometries to remove topography effects from the data. The analogue, analytical, and numerical solution methods were used to study the analogue model (Wescott and Hessler, 1962; Faradzhev et al., 1972). Various 2D numerical techniques have been used for the numerical treatment of topographic effects, such as networking analogy (Ku et al., 1973; Ngco, 1980) and Rayleigh scattering numerical modelling techniques (Reddig and Jiracek, 1984; Jiracek et al., 1989), the finite-element method (Wannamaker et al., 1986; Franke et al., 2007), and the finite-difference method (Pek and Verner, 1996; Sasaki, 2003; Tyagi, 2007). The distortions in MT data due to topography and near-surface inhomogeneities have been observed by many researchers (Chouteau and Bouchard, 1988; Jiracek, 1990; Vozoff, 1991; Rijo, 1977; Ward et al., 1973). The distortion tensor stripping-off technique has been used to reduce the topographic effect and to remove distortion due to the near-surface heterogeneity (Larsen, 1977). The analogue, analytical, and numerical solution methods were used to study the analogue model (Wescott and Hessler, 1962; Faradzhev et al., 1972). Various 2D numerical techniques have been used for the numerical treatment of the topographic effects, such as networking analogy (Ku et al., 1973; Ngoc, 1980) and Rayleigh scattering numerical modelling techniques (Jiracek et al., 1989) and finite-element method (Wannamaker et al., 1986; Franke et al., 2007). In 2D, the topography effect is galvanic in transverse magnetic (TM) mode and inductive in transverse electric (TE) mode; hence, there is more distortion in the TM mode than in the TE mode (Gurer and Ilkisik, 1997; Kumar et al., 2014, 2018, 2022; Kunetz and DeGery, 1956).
In this study, a modified 2D forward algorithm and an inversion modelling code (EM2INV) (Rastogi, 1997) based on the finite-difference method were used to compute MT forward modelling responses over flat earth and topographic surfaces. Two different terrain correction procedures have been used in this study to compute the topography distortion for a synthetic model of the Garhwal Himalayan region (Roorkee–Gangotri section): the first correction procedure was adopted from Chouteau and Bouchard (1988) and the second was adopted from Nam et al. (2008). The results of both terrain correction procedures have been compared with the model used by Chouteau and Bouchard (1988).
As stated above, topography correction was applied to MT data using two different techniques. The first technique was introduced by Chouteau and Bouchard (1988) to estimate the distortion tensor and the correction of MT data before data inversion. In the second approach, the distortion tensor stripping-off technique was used to remove distortion from MT data (Larsen, 1977; Nam et al., 2008). Thus, two correction procedures, the first adopted by Chouteau and Bouchard (1988) and the second by Nam et al. (2008), were used to correct the MT data.
2.1 Terrain correction procedure 1 (TCP1)
The computational algorithm for 2D forward modelling has been used to account for irregular terrain. The distortion tensor for the topographic effect was calculated using the technique adopted by Chouteau and Bouchard (1988). This calculation is based on the assumption that the topography-distorted subsurface field can be approximated by multiplying the distortion tensor by the subsurface field for a flat earth, as follows:
where and are the distorted and normal electric field matrices with elements E(f,r)D and E(f,r)N respectively. D is the distortion tensor with elements D(f,r), where f is frequency and r is the measuring site position. For a 2D problem in TM mode with an x axis in the strike direction, Eq. (1) can be written as follows:
The impedance tensor can be calculated by dividing Eq. (2) by the magnetic field HY.
where ZN(f,x) and ZD(f,x) are the normal (flat-earth) impedance and distortion impedance respectively. The complex coefficients D(f,x) are distortion coefficients that should just reflect the topography effect. The distortion coefficients are calculated by normalizing the impedances Zt(f,x) computed over the topographic model above a homogeneous medium with the half-space impedance. Thus, the corrected impedance over flat earth can be calculated by taking the following ratio of the observed impedances, ZD(f,x), over irregular topography to the distortion coefficients D(f,x):
where ZC(f,x) is terrain-corrected impedance.
2.2 Terrain correction procedure 2 (TCP2)
In this correction procedure, the MT data were corrected using the technique adopted by Nam et al. (2008). Larsen (1977) introduced the distortion tensor stripping-off technique, in which the undistorted impedance tensor can be calculated using a linear relationship between the distorted and undistorted impedance tensor, and the topography-distorted MT data can be corrected by computing the distortion tensor. The undistorted impedance tensor is linearly related to the distorted impedance tensor as follows:
where ZD is the distortion impedance tensor, DZ is the distortion tensor, and ZU is the undistorted impedance tensor. The distortion tensor can be calculated from the relation between the impedance tensor for a homogeneous medium with earth surface topography (Zt) and that with a flat-earth surface (Zh), as follows:
For 2D, and , the inhomogeneous earth distortion tensor, Eqs. (5) and (6) can be rewritten in matrix form as
and
Thus,
Substituting Eq. (10) in Eq. (7),
The undistorted or corrected impedance tensor component can be obtained as follows:
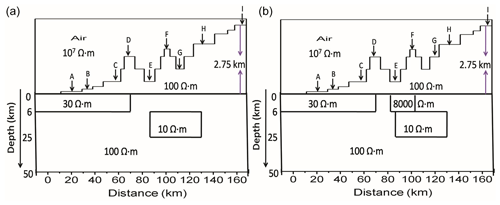
In this study, we replicated the model of Chouteau and Bouchard (1988). A 2D topographic homogeneous model of 500 Ω m half-space with a resistive block of 10 kΩ m and a thickness of 1 km was embedded in the model from surface relief (Fig. 1). The MT responses for the model were computed with and without topography. The terrain correction procedures (TCP1 and TCP2) were applied to the model responses at a particular period of 0.1 s and validated over the inhomogeneous model of Chouteau and Bouchard (1988). The two topography-corrected responses were analysed at nine different sites (denoted by A, B, C, D, E, F, G, H, and I), as shown in Fig. 1, for six distinct time periods (0.001, 0.01, 0.1, 1, 10, and 100 s). In 2D, the topography effect is galvanic in TM mode and inductive in TE mode. Therefore, a comparison of the TM component of flat-earth response (FER), topographic response (TR), and two terrain correction responses (TCR1 and TCR2) is shown in Fig. 2. It is concluded from Fig. 2 that TCR1 and TCR2 are very similar to the FER at a particular period of 0.1 s but not similar to the TR, which shows good agreement with the published results of Chouteau and Bouchard (1988).
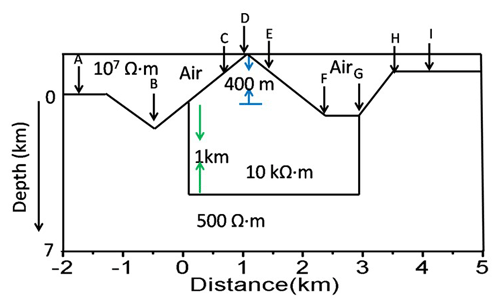
Figure 1Topographic model of a 500 Ω m half-space with a resistive body of 10 kΩ m that was embedded from the surface relief (Chouteau and Bouchard, 1988).
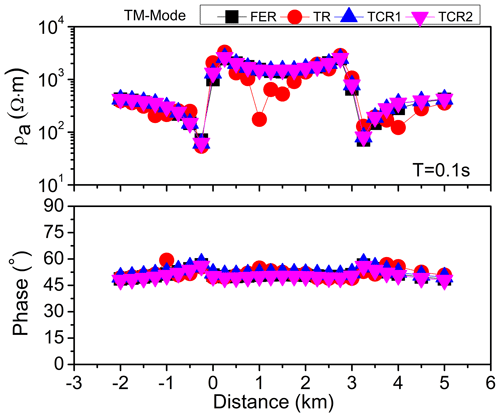
Figure 2Comparison of the TM component of the flat-earth response (FER), topographic response (TR), and two terrain correction responses (TCR1 and TCR2) at 0.1 s.
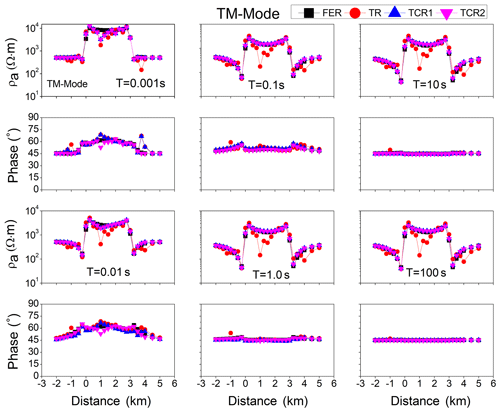
Figure 3Comparison of the TM component of the flat-earth response (FER), topographic response (TR), and two correction procedures (TCR1 and TCR2) for the model in Fig. 1 for six different periods (0.001, 0.01, 0.1, 1, 10, and 100 s).
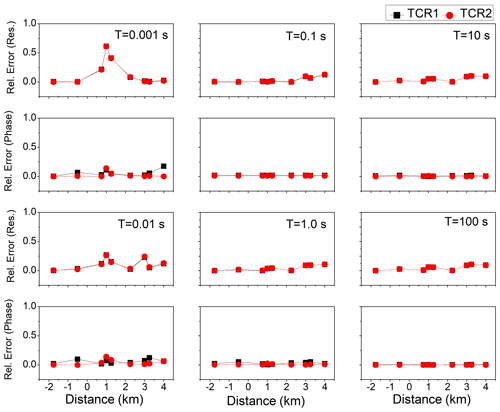
Figure 3 shows that the topography distortions are large for a longer period in the apparent resistivity component only, which presents the galvanic nature of the topography distortions. The terrain-corrected responses (TCR1 and TCR2) in Fig. 3 are almost similar to FERs for six respective periods (0.001, 0.01, 0.1, 1, 10, and 100 s). Relative errors were also calculated to check the accuracy of the terrain correction responses (TCR1 and TCR2) against FERs for these periods. The relative error between the FERs and TCR1 and TCR2 were very small for all periods except at site D only for shorter periods (because of the 10 kΩ m resistive body), as shown in Fig. 4. This shows the accuracy of the correction procedures.
A theoretical analysis of the effect of topography on MT responses was also taken into account in the Himalayan topography model. A theoretical model of the Roorkee–Gangotri profile was generated to simulate the MT response. To compute the MT forward modelling responses over a rugged topographic surface in the Roorkee–Gangotri section, the input model was prepared from a 2D inverted geoelectrical resistivity model (Tyagi, 2007). The topography model, with an elevation of 2.75 km, consists of a 180 km long profile drawn from Roorkee to Gangotri (Tyagi, 2007; Suman et al., 2023). In this model, two conductive blocks with a respective resistivity of 30 and 10 Ω m were embedded in a homogeneous half-space of 100 Ω m resistivity. The first block of 30 Ω m resistivity with a width of 80 km and a thickness of 6 km was embedded just near the Earth's surface relief and the second block of width 40 km and a thickness 25 km was embedded at 6 km depth from the surface. The MT responses were computed by considering three models: (1) one with a half-space of 100 Ω m resistivity (Fig. 5a), (2) one with a half-space of 500 Ω m resistivity, and (3) one with an additional resistive body of 8000 Ω m embedded from Earth's surface relief with a thickness of about 6 km and a half-space of 100 Ω m resistivity, as shown in Fig. 5b. The TR, FER, and two topography-corrected responses (TCR1 and TCR2) were analysed for nine sites (A, B, C, D, E, F, G, H, and I), as shown in Fig. 5, for six distinct periods (0.0013, 0.0102, 0.1063, 1.1110, 11.6078, and 121.2813 s).
5.1 Model with a half-space of 100 Ω m resistivity
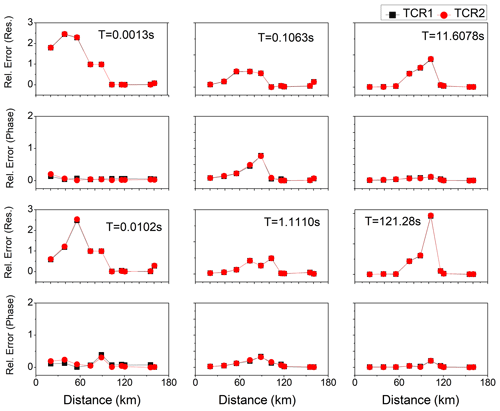
The TR and FER were computed for the topography model with a conductive body of 30 Ω m resistivity in a half-space of 100 Ω m resistivity (Fig. 5a), and the topography corrections procedures were applied to the MT data. Figure 6 shows the TM mode of TR, FER, and two topography correction responses (TCR1 and TCR2) for six different periods (0.0013, 0.0102, 0.1063, 1.1110, 11.6078, and 121.2813 s). The topography effect depends upon the ramp/slope angle of the hill and is significant when the slope angle is greater than 7.5° (Kumar et al., 2018). It is clear from Fig. 6 that the TCR1 and TCR2 are almost similar to the TR, as the slope angle is less than 1°. The TCR1 and TCR2 were not similar to the FER for the sites from A to D for the shorter periods of 0.0013, 0.0102, 0.1063, and 1.1110 s, due to the exposure of the conductive body with 30 Ω m resistivity to the surface (from A to D) and its galvanic effect. The relative errors were also calculated between the FER with TCR1 and TCR2: they were high for the sites A, B, and C for shorter periods (0.0013, 0.0102, and 0.1063 s), due to the presence of the conductive body underneath these sites, and very small for all other sites (D, E, F, G, H, and I) for all periods, as shown in Fig. 7.
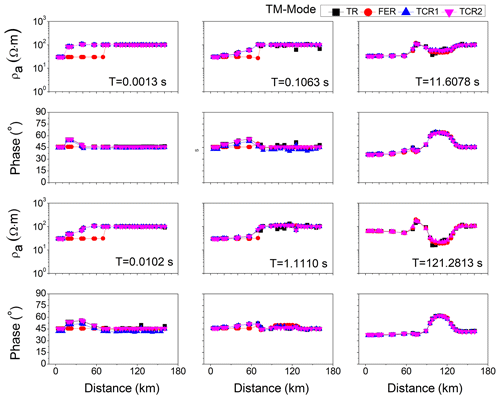
Figure 6Comparison of the TM components of flat-earth response (FER), topographic response (TR), and two correction procedures (TCR1 and TCR2) for six different periods for a homogeneous half-space of 100 Ω m resistivity.
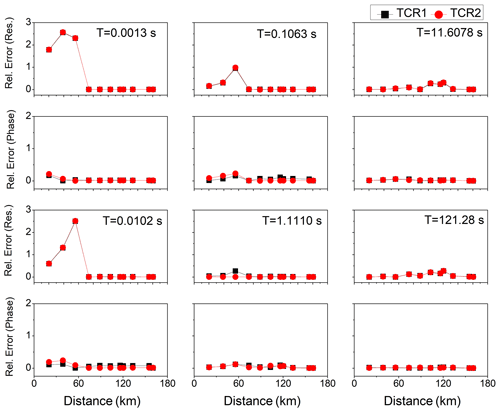
Figure 7Relative error between the terrain-corrected responses (TCR1 and TCR2) with respect to the flat-earth response (apparent resistivity and phase) for six different periods with a half-space of 100 Ω m resistivity.
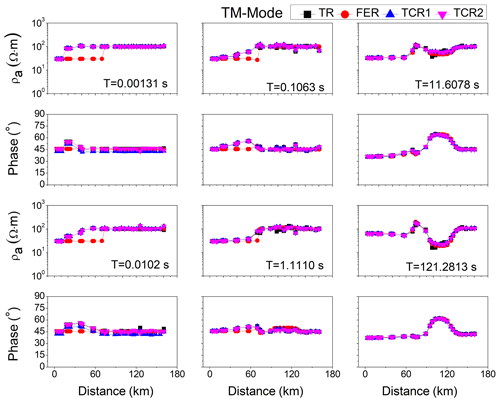
Figure 8Comparison of the TM components of flat-earth response (FER), topographic response (TR), and two correction procedures (TCR1 and TCR2) for six different periods for a half-space of 500 Ω m resistivity.
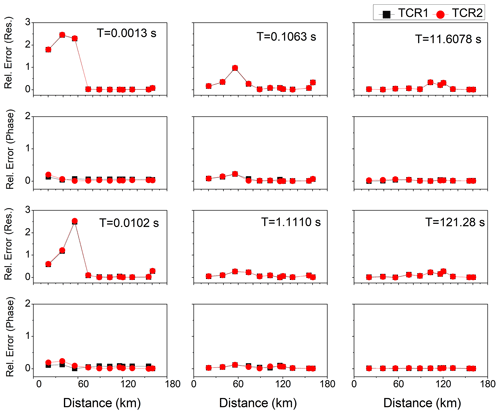
Figure 9Relative error between the terrain-corrected responses (TCR1 and TCR2) with respect to the flat-earth response (apparent resistivity and phase) for six different periods with a half-space of 500 Ω m resistivity.
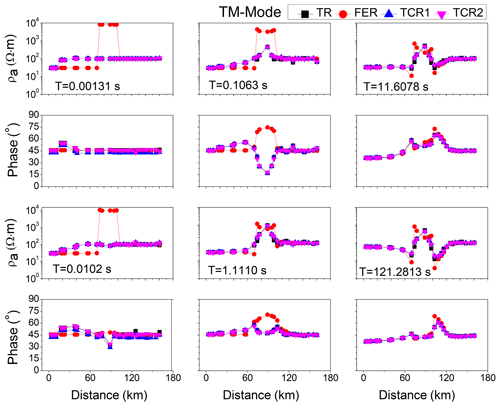
Figure 10Comparison of the TM components of flat-earth response (FER), topographic response (TR), and two correction procedures (TCR1 and TCR2) for six different periods for a half-space of 100 Ω m resistivity.
5.2 Model with a half-space of 500 Ω m resistivity
Now consider the case in which model half-space resistivity was replaced with 500 Ω m in Fig. 5a. The TR and FER were computed for the topography model with a half-space of 500 Ω m resistivity (Fig. 5a), and the topography correction procedures were applied to the MT data. Figure 8 shows the TM component of TR, FER, and topography-corrected responses (TCR1 and TCR 2) for six different periods. The results were almost similar to the response of the model with a half-space of 100 Ω m resistivity. The relative errors were also calculated in this case between the FER with TCR1 and TCR2, and the results were similar to the model with a half-space of 100 Ω m resistivity for all periods (0.0013, 0.0102, 0.1063, 1.1110, 11.6078, and 121.2813 s), as shown in Fig. 9.
5.3 Model with a resistive block of 8000 Ω m resistivity in a half-space of 100 Ω m resistivity
The TR and FER were also computed for the topography model with a resistive block of 8000 Ω m resistivity in a half-space of 100 Ω m resistivity (Fig. 5b), and the topography corrections were applied to the MT data. Figure 10 shows the TM component of TR, FER, and two topography correction responses (TCR1 and TCR2) for six different periods. The TCR1 and TCR2 were not similar to the flat-earth model for the sites from A to F, due to the exposure of the conductive body with a 30 Ω m resistivity to the surface (from A to D) and its galvanic effect as well as the presence of a 8000 Ω m resistive body (from D to F). The relative errors were also calculated between the FER with TCR1 and TCR2 and were high for the sites A, B, and C for shorter periods (0.0013, 0.0102, and 0.1063 s), due to the presence of the conductive body underneath these sites, and for longer periods (1.1110, 11.6078, and 121.2813 s), due to the presence of an 8000 Ω m resistive body from D to F, as shown in Fig. 11.
The study shows the effect of topography in the MT data along a synthetic model of the Roorkee–Gangotri profile. Two correction procedures were used to remove the topography distortion from MT data. The similar FER, TCR1, and TCR2 in Fig. 3 show that both correction procedures are capable of removing the topography effect and, thus, confirms the accuracy of the two correction procedures. The similar TR, TCR1, and TCR2 responses (Figs. 6, 8, 10) concluded that there is no need for topography correction along the Roorkee–Gangotri profile, as the slope angle is less than 1°. The relative error between the FER and TCR1 and TCR2 also showed the accuracy of the two correction procedures (TCR1 and TCR2) in this study. The presence of near-surface heterogeneity/surface exposure of conductive/resistive body also distorts the MT responses in this model (the FER is not similar to TR, TCR1, and TCR2).
The software code used in this work was the EM2INV inversion modelling code, written in Fortran, based on the finite-difference method. The code is available upon request from the authors.
The data that support the findings of this study are available from the corresponding author (Suman Saini) upon reasonable request.
DKT and SS designed the experiments, developed the model, and performed the simulations. RS and SK prepared the manuscript with contributions from all co-authors.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Suman Saini is grateful to the head of department of the Department of Physics, M. M. Engineering College, Maharishi Markandeshwar (Deemed to be University), for continuous guidance and support during this research.
This paper was edited by Luciano Telesca and reviewed by Linjiang Qin and one anonymous referee.
Cagniard, L.: Basic theory of the magneto-telluric method of geophysical prospecting, Geophysics, 18, 605–635, 1953.
Changhong, L.: The effects of 3D topography on controlled-source audio-frequency magnetotelluric responses, Geophysics, 83, Wb97–wb108, https://doi.org/10.1190/geo2017-0429.1, 2018.
Chouteau, M. and Bouchard, K.: Two-dimensional terrain correction in magnetotelluric Surveys, Geophysics, 53, 854–862, 1988.
Coggon, H.: Electromagnetic and electrical modeling by the finite-element method, Geophysics, 36, 132–155, 1971.
Faradzhev, A. S., Kakhramanov, K. K., Sarkisov, G. A., and Khalilova, N. E.: On effects of terrain on magnetotelluric sounding (MTS) and profiling (MTP), Izvestia Earth Physics, 5, 329–330, 1972.
Franke, A., Börner, R. U., and Spitzer, K.: Adaptive unstructured grid finite element simulation of two-dimensional magnetotelluric fields for arbitrary surface and seafloor topography, Geophys. J. Int., 171, 71–86, 2007.
Gurer, A. and Ilkisik, M.: The importance of topographic corrections on magnetotelluric response data from rugged regions of Anatolia, Geophys. Prospect., 45, 111–125, 1997.
Harinarayana, T. and Sarma, S. V. S.: Topographic effects on telluric field measurements, Pageoph., 120, 778–783, 1982.
Israil, M., Tyagi, D. K., Gupta, P. K., and Niwas, S.: Magnetotelluric investigations for imaging electrical structure of Garhwal Himalaya corridor, Uttarakhand, India, J. Earth Syst. Sci., 117, 189–200, 2008.
Israil, M., Mamoriya, P., Gupta, P. K., and Varshney, S. K.: Transverse Tectonics Feature Delineated by Modelling of Magnetotelluric Data from Garhwal Himalaya Corridor, India. Curr. Sci., 111, 868–875, 2016.
Jiracek, G.: Near-surface and topographic distortions in electromagnetic induction, Surv. Geophys., 11, 163–203, 1990.
Jiracek, G. R., Redding, R. P., and Kojima, R. K.: Application of the Rayleigh-FFT techniquetomagnetotelluric modeling and correction, Phys. Earth Planet. In., 53, 365–375, 1989.
Konda, S., Patro, P. K., Reddy, K. C., and Babu, N.: Three-dimensional magnetotelluric signatures and rheology of subducting continental crust: Insights from Sikkim Himalaya, India, J. Geodynam., 155, 101961, https://doi.org/10.1016/j.jog.2023.101961, 2023.
Ku, C. C., Hsieh, M. S., and Lim, S. H.: The topographic effect in electromagnetic fields, Can. J. Earth Sci., 10, 645–656, 1973.
Kumar, D., Singh, A., and Israil, M.: Necessity of Terrain Correction in Magnetotelluric Data Recorded from Garhwal Himalayan Region, India, Geosciences, 11, 482, https://doi.org/10.3390/geosciences11110482, 2021.
Kumar, G. P., Manglik, A., and Thiagarajan, S.:Crustal Geoelectric Structure of the Sikkim Himalaya and Adjoining Gangetic Foreland Basin, Tech. Phys., 637, 238–250, 2014.
Kumar, S., Patro, P. K., and Chaudhary, B. S.: Three dimensional topography correction applied to magnetotelluric data from Sikkim Himalayas, Phys. Earth Planet. In., 279, 33–46, 2018.
Kumar, S., Patro, K. P., and Chaudhary, B. S.: Subsurface Resistivity Image of Sikkim Himalaya as Derived from Topography Corrected Magnetotelluric Data, J. Geol. Soc. India, 98, 335–343, https://doi.org/10.1007/s12594-022-1985-2, 2022.
Kunetz, G. and DeGery, J. C.: Examples d'application de la representation conform al'interpretation du champ tellurique, Revue De L'institut Français Du Pétrolle, 11, 1179–1192, 1956.
Larsen, J. C.: Removal of local surface conductivity effects from low frequency mantle response curves, ActaGeodaet, Geophys. Montanist. Acad. Sci. Hung. Tomus., 12, 183–186, 1977.
Mohan, K., Kumar, G. P., Chaudhary, P., Choudhary, V. K., Nagar, M., Khuswaha, D., Patel, P., Gandhi, D., and Rastogi, B. K.: Magnetotelluric Investigations to Identify Geothermal Source Zone near ChabsarHotwater Spring Site, Ahmedabad, Gujarat, Northwest India, Geothermics, 65, 198–209, 2017.
Nam, M. J., Kim, H. J., Song, Y., Lee, T. J., Son, J. S., and Suh, J. H.: Three-dimensional topography corrections of magnetotelluric data, Geophys. J. Int., 174, 464–474, 2008.
Ngoc, P. V.: Magnetotelluric survey of the Mount Meager region of the Squamish Valley (British Colombia). Geomagnetic Service of Canada, Earth Physics Branch of the Dept. of Energy, Mines and Resources of Canada, Rep., 80-8-E, 1980.
Patro, P. K.: Magnetotelluric Studies for Hydrocarbon and Geothermal Resources: Examples from the Asian Region, Surv. Geophys., 38, 1005–1041, 2017.
Patro, P. K. and Harinarayana, T.: Deep Geoelectric Structure of the Sikkim Himalayas (NE India) Using Magnetotelluric Studies, Phys. Earth Planet. In., 173, 171–176, 2009.
Pek, J. and Verner, T.: Finite-difference modelling of magnetotelluric fields in two-dimensional anisotropic media, Geophys. J. Int., 128, 505–521, 1997.
Rastogi, A.: A finite difference algorithm for two-dimensional inversion of geo-electromagneticdata, Ph.D. Thesis, University of Roorkee, India, 1997.
Reddig, R. P. and Jiracek, G. R.: Topographic modeling and correction in magnetotellurics, in: 54th Annual International Meeting, Society of Exploration Geophysicists, Expanded Abstract, 44–47, 1984.
Rijo, L.: Modelling of electric and electromagnetic data, Ph.D. thesis, Univ. of Utah., 19, 1977.
Sasaki, Y.: 3-D electromagnetic modelling and inversion incorporating topography, ASEG Extended Abstracts, 1, 1–7, https://doi.org/10.1071/ASEG2003_3DEMab013, 2003.
Suman, S., Tyagi, D. K., and Sherawat, R.: Topography distortion effect on Magnetotelluric (MT) profiling of Sub-Himalayan region using two-dimensional modelling, J. Integr. Sci. Technol., 11, 462, NBN:sciencein.jist.2023.v11.462, 2023.
Thayer, R. E.: Topographic distortion of telluric currents: a simple calculation, Geophysics, 40, 91–95, 1975.
Tikhonov, A. N.: Determination of the Electrical Characteristics of the Deep Strata of the Earth's Crust, DoklAkadamiaNauk, 73, 295–297, 1950.
Tyagi, D. K.: 2D modeling and inversion of magnetotelluric data acquired in Garhwal Himalaya, Ph.D. Thesis, Indian Institute of Technology Roorkee, India, 2007.
Vozoff, K.: The magnetotelluric method, in: Electromagnetic Methods in Applied Geophysics, edited by: Nabighian, M. N., Society of Exploration Geophysicists, 2, 641–711, 1991.
Wannamaker, P. E., Stodt, J. A., and Rijo, L.: Two-dimensional topographic responses in magnetotellurics modeled using finite elements, Geophysics, 51, 2131–2144, 1986.
Ward, S. H., Peeples, W. J., and Ryu, J.: Analysis of geo-electromagnetic data, Meth. Compo Phys., 13, 163–238, 1973.
Wescott, E. M. and Hessler, V. P.: The effect of topography and geology on telluric currents, J. Geophys. Res., 67, 4813–4823, 1962.
Xiong, B., Luo, T. Y., Chen, L. W., Dai, S. K., Xu, Z. F., Li, C. W., Ding, Y. L., Wang, H. H., and Li, J. H.: Influence of Complex Topography on Magnetotelluric Observed Data Using Three-Dimensional Numerical Simulation: A Case from Guangxi Area, China, Appl. Geophys., 17, 601–615, 2020.
Zhang, K., Wei, W., Lu, Q., Dong, H., and Li, Y.: Theoretical Assessment of 3-D Magnetotelluric Method for Oil and Gas Exploration: Synthetic Examples, J. Appl. Geophys., 106, 23–36, 2014.