the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Brief communication: Lower-bound estimates for residence time of energy in the atmospheres of Venus, Mars and Titan
Javier Pelegrina
Amalio Fernández-Pacheco
The residence time of energy in a planetary atmosphere, τ, which was recently introduced and computed for the Earth's atmosphere (Osácar et al., 2020), is here extended to the atmospheres of Venus, Mars and Titan. τ is the timescale for the energy transport across the atmosphere. In the cases of Venus, Mars and Titan, these computations are lower bounds due to a lack of some energy data. If the analogy between τ and the solar Kelvin–Helmholtz scale is assumed, then τ would also be the time the atmosphere needs to return to equilibrium after a global thermal perturbation.
- Article
(109 KB) - Full-text XML
- BibTeX
- EndNote
When the inflow, ℱi, of any substance into a box is equal to the outflow, ℱo, then the amount of that substance in the box, ℳ, is constant. This constitutes an equilibrium or steady state. Then, the ratio of the stock in the box to the flow rate (in or out) is called residence time and is a timescale for the transport of the substance in the box.
In Eq. (1) it is assumed that the substance is conserved. A good example of this type is the parameter defined in atmospheric chemistry (Hobbs, 2000) as the average residence time of each individual gas, defined as Eq. (1). ℳ is the total average mass of the gas in the atmosphere, and ℱ is the total average influx or outflux, which in time average for the whole atmosphere are equal.
In this work we extend the substance that flows in the box from matter to energy, and the residence time is
where E is the total energy in the box (a planetary atmosphere), and F is the energy flux that enters or leaves it.
Here, by using Eq. (2), we estimate the average residence time of energy in several planetary atmospheres. Planetary atmospheres constitute steady-state problems, because the storage of energy in their interior is not systematically increasing or decreasing. Several authors have previously considered the energy–residence-time relation in other types of problems (Mcilveen, 1992, 2010; Harte, 1988).
The structure of this communication is the following: Sect. 2 addresses the numerator of Eq. (2) E, while Sect. 3 deals with the denominator F. In Sect. 4 the residence time of energy is considered for the Sun. The paper concludes with a discussion (Sect. 5).
The most important forms of energy in an atmosphere are the thermodynamic internal energy, U; the potential energy due to the planet's gravity, P; the kinetic energy, K; and the latent energy, L, related to the phase transitions.
In a planar atmosphere, in hydrostatic equilibrium and by using the state equation for an ideal gas, the first two quantities can be written as
In Eqs. (3) and (4), cv is the specific heat at constant volume, R is the gas constant, and ρ(z) and T(z) are the density and temperature of the mixture of gases of the atmosphere, respectively. E stands for the total energy in the atmosphere:
The sum will be called dry static energy; then
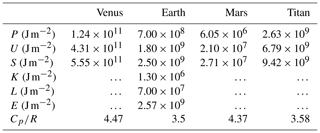
It is important to remark that S is much bigger than the sum K+L. For example, for the Earth (Peixoto and Oort, 1992)
In the case of Earth's atmosphere, the four terms U, P, K and L (and hence E) are well approximated (Peixoto and Oort, 1992). However, for the atmospheres of Venus, Mars and Titan we can only compute the terms U and P and estimate S but not E. We have carried out these computations by performing the numerical integration (Eq. 4), using the vertical data p(z) shown in (Sánchez-Lavega, 2011, p. 212–227). The results of E or S for each planet are shown in Table 1.
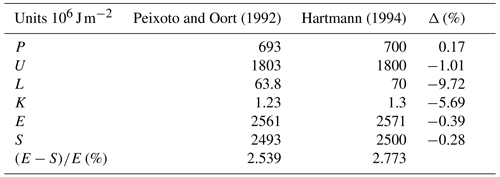
For the Earth's atmosphere, the estimates of different authors are very similar. Table 2 compares values of Peixoto and Oort (1992) and Hartmann (1994). The last row corresponds to the difference between the total energy of the Earth's atmosphere (E) and its dry static energy (S). The kinetic and latent components can be neglected in a first approximation.
Peixoto and Oort (1992)Hartmann (1994)The sound velocity of an ideal gas is
where R∗ is the universal constant of gases, and M is the molecular mass of the gas; is the adiabatic constant, and T is the temperature. The sound velocity can be used to estimate the ratio between K and S.
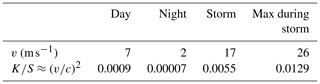
In the case of Mars, on the surface c = 228.73 m s−1. Table 3 contains data of winds measured by Viking probes on the surface (Sheehan, 1996, p. 194). With these data, K can be neglected in Mars. In the case of Titan, Mitchell (2011) assumes that the kinetic energy can be neglected. Based on these figures, the kinetic energy can be omitted in a first approximation for Mars and Titan.
In the case when S is not much bigger than K+L, our results for τ would be a lower bound. Future observations will determine these numbers.
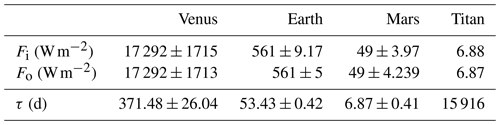
The values of the energy fluxes for all planets have been deduced from Read et al. (2016). For each planet, Fi and Fo represent the inflow and outflow of energy absorbed or emitted by the atmospheres. The so-called “Trenberth diagrams” (Kiehl and Trenberth, 1997; Read et al., 2016) are particularly suited to the identification of these fluxes.
As an example, in the case of Venus (see Read et al., 2016, Fig. 6), the fluxes absorbed by the atmosphere (Fi) are 135 W m−2 from incoming solar radiation (shortwave) absorbed in the middle atmosphere, 3 W m−2 from incoming solar radiation absorbed by the lower atmosphere and 17 154 W m−2 of longwave flux absorbed from surface. Thus, the total influx is 17 292 W m−2.
The emitted fluxes (Fo) are 17 132 W m−2 of longwave radiation to surface and 160 W m−2 of longwave radiation emitted from atmosphere to space. The total outflux value is 17 292 W m−2. Analogous calculations for the rest of the planets give the values for Fi and Fo shown in Table 4.
These energy fluxes were computed by Read et al. (2016) through complex and detailed numerical models. Their results coincide well with observations and have little uncertainty, so its effect on the residence time of energy is small. In any case, here we have computed that uncertainty value.
For Earth, quoting Read et al. (2016, p. 704), “Figure 1 thus represents the current state of the art in deriving such an energy budget for an entire planet.” Although Read et al. (2016) do not give exact numbers for uncertainty of energy fluxes, their references herein do. We have computed the following uncertainty values: Fin = 561 ± 9.17 W m−2 ⇒ τ = 53.43 ± 0.87 d, and Fout = 561 ± 5 W m−2 ⇒ τ = 53.43 ± 0.48 d. We note how both fluxes and residence times are extremely similar and compatible. A weighted average would give us τ = 53.43 ± 0.42 d.
When computing the energy fluxes of Mars, Read et al. (2016) use a detailed radiative transfer model “suggesting an uncertainty in infrared fluxes of around 6 %–12 %”. By using the worst-case scenario of a 12 % uncertainty, we obtain Fin = 49 ± 3.97 W m−2 ⇒ τ = 6.87 ± 0.56 d, and Fout = 49 ± 4.23 W m−2 ⇒ τ = 53.43 ± 0.59 d. This gives us τ = 6.87 ± 0.41 d. These uncertainties are reflected in Table 4.
About the energy fluxes in Venus, Read et al. (2016) state, “energy fluxes agree with available observations to around ± 10 %”. However, they admit that “the energy budget presented … should therefore be seen as a plausible scheme that is internally self-consistent and representative of a reasonably good radiative–dynamical model of the Venus atmosphere in equilibrium”. Assuming an uncertainty of 10 % in energy fluxes, Fin = 17 292 ± 1715 W m−2 ⇒ τ = 371.48 ± 36.84 d, and Fout = 17 292 ± 1713 W m−2 ⇒ τ = 371.48 ± 36.80 d. This gives τ = 371.48 ± 26.04 d.
In Titan's energy fluxes, Read et al. (2016) do not state any bound on uncertainties. However, they say (Read et al., 2016, p. 711) “energy fluxes are consistent with the measurements of Li et al. (2011) to within a few per cent, although the internal and surface fluxes are not well constrained by observations.” We can assume that the energy fluxes they present and used here are fairly accurate with low uncertainty.
With the total energy values, E or S (in Table 1) and F (Table 4), we estimate the value of residence time of energy in the atmosphere of each planet. However, as we stressed above, strictly speaking E is only known in the Earth's case. In the other three cases, the ratio is a lower bound for the actual residence time.
These results and their estimated uncertainties are shown in Table 4.
Although the physics in the solar interior greatly differs from that of a planetary atmosphere, we have considered it convenient to introduce this section because of the parallelism that exists between the atmospheric τ and the solar Kelvin–Helmoholtz timescale.
where G is the gravitational constant, and M⊙, R⊙ and L⊙ stand for the solar mass, radius and radiant flux.
The Sun is in a steady state for the energy. The temperatures in its interior are not systematically increasing or decreasing. In Stix (2003) it is shown that the Kelvin–Helmholtz timescale (KH) corresponds to both the time that a photon takes from the core until it leaves the surface and the time necessary for the star to return to equilibrium after a global perturbation.
As τKH is the ratio between stored energy and its flux, it also can be considered a residence time of energy in the Sun (for details, see Osácar et al., 2020). Furthermore, Spruit (2000) shows that KH is the longest timescale for any solar perturbations.
In summary, if the analogy between the solar KH and the atmospheric τ is assumed, then τ is not only the timescale for the energy transport in the atmosphere but also the timescale the atmosphere needs to return to equilibrium after a global thermal perturbation. Furthermore, τ is the longest timescale for any atmospheric perturbation.
As we concluded in Sect. 4, τ may not only be the mean time it takes for the energy to enter and leave the atmosphere; it may also be the time needed to return to equilibrium after a global thermal perturbation. Although this is likely the case, it does not constitute a proof. But, if this analogy is accepted, it imposes the condition that τ has to be greater than any other relaxation timescale.
In this section, we will introduce the so-called radiative relaxation time, τR, and we will explore if the inequality τ>τR holds.
In general, if an atmospheric state at equilibrium is perturbed, the atmosphere uses the most efficient mechanism at hand to neutralize it. Typically, this mechanism can be convective, advective or radiative. The radiative relaxation timescale, τR, is the time it would take to relax the perturbation by radiating the energy excess in the infrared. This timescale is often found in the literature (e.g. Houghton, 2002; Wells, 2012; Sánchez-Lavega, 2011).
The computation of this timescale τR is done by a perturbative method (see, for example, Wells, 2012) and gives
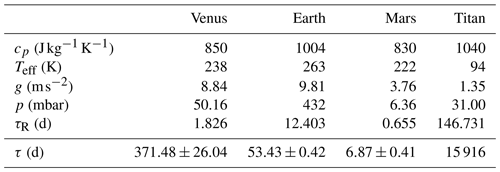
In this expression, cp is the specific heat at constant pressure, g is gravity and σ is the Stefan–Boltzmann constant. Teff is the blackbody effective temperature of the planet, and p is the pressure at the height where the computation is performed.
Due to the factor p in the numerator of Eq. (12), the value of τR decreases rapidly with height. Therefore, radiation is not an efficient mechanism to neutralize perturbations in the low troposphere. In that region, τR is thus very long. The low troposphere is dominated by convective movements. We find a clear example of these phenomena in Venus, where τR varies from 116 d at 40 km (lower cloud deck) to 0.5 h at 100 km (Sánchez-Lavega et al., 2017).
Since about 80 % of radiative flux leaving an atmosphere comes from the cold top of the highest atmospheric opaque layer, we have estimated τR at the height of maximum emission, p=pr, which is the pressure at the height where T=Teff.
In Table 5 we show the results for τR in the case of Venus, Earth, Mars and Titan, as well as the data used for calculating them. The data for this table were obtained from Sánchez-Lavega (2011). The values for energy residence time τ are those from the last row of Table 4. In the four cases, the radiative timescale τR is shorter than the time of energy residence τ.
If, in any of the planets, the quoted values of τ were a lower bound, as commented in Sect. 2, then the inequality τ>τR would be strengthened.
The data of the energies used for the estimation of residence time in the Venus, Earth, Mars and Titan atmospheres were computed with p and T from Sánchez-Lavega (2011, p. 212–227). The fluxes of energy for all the cases were deduced from Read et al. (2016, https://doi.org/10.1002/qj.2704). The data for the calculation of τR were obtained from Sánchez-Lavega (2011).
AFP conceived the idea, and CO, JP and AFP wrote the paper.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper was edited by Zoltan Toth and reviewed by two anonymous referees.
Harte, J.: Consider a Spherical Cow, University Science Books, Sausalito, California, USA, 1988. a
Hartmann, D. L.: Global Physics Climatology, Academic Press, San Diego, California, USA, 1994. a, b
Hobbs, P.: Introduction to Atmospheric Chemistry, 2nd edn., Cambridge University Press, Cambridge, UK, 2000. a
Houghton, J.: The Physics of the Atmosphere, Cambridge University Press, Cambridge, UK, 2002. a
Kiehl, J. and Trenberth, K.: Earth's annual global mean energy budget, B. Am. Meteorol. Soc., 78, 197–208, 1997. a
Mcilveen, R.: Fundamentals of Weather and Climate, 1st edn., Chapman and Hall, London, UK, 1992. a
Mcilveen, R.: Fundamentals of Weather and Climate, 2nd edn., Oxford, Oxford, UK, 2010. a
Mitchell, J. L.: Titan's transport-driven methane cycle, Astrophys. J. Lett., 756, 1–5, https://doi.org/10.1088/2041-8205/756/2/L26, 2011. a
Osácar, C., Membrado, M., and Fernández-Pacheco, A.: Brief communication: Residence time of energy in the atmosphere, Nonlin. Processes Geophys., 27, 235–237, https://doi.org/10.5194/npg-27-235-2020, 2020. a, b
Peixoto, J. and Oort, H.: Physics of Climate, AJP, NewYork, USA, 1992. a, b, c, d
Read, P. L., Barstow, J., Charnay, B., Chelvaniththilan, S., Irwin, P. G. J., Knight, S., Lebonnois, S., Lewis, S. R., Mendonça, J., and Montabone, L.: Global energy budgets and 'Trenberth diagrams' for the climates of terrestrial and gas giant planets, Q. J. Roy. Meteor. Soc., 142, 703–720, https://doi.org/10.1002/qj.2704, 2016. a, b, c, d, e, f, g, h, i, j, k
Sánchez-Lavega, A.: An Introduction to Planetary Atmospheres, Taylor and Francis, Boca Raton, Florida, USA, 2011. a, b, c, d, e
Sánchez-Lavega, A., Lebonnois, S., Imamura, T., Read, P., and Luz, D.: The Atmospheric Dynamics of Venus, Space Sci. Rev., 202, 1541–1616, https://doi.org/10.1007/s11214-017-0389-x, 2017. a
Sheehan, W.: The Planet Mars: A History of Observation and Discovery, University of Arizona Press, Phoenix, Arizona, USA, 1996. a
Spruit, H.: Theory of solar irradiance variations, Space Sci. Rev., 94, 113–126, https://doi.org/10.1023/A:1026742519353, 2000. a
Stix, M.: On the time scale of the energy transport in the Sun, Sol. Phys., 212, 3–6, 2003. a
Wells, N. C.: Physics of the Atmosphere and the Ocean, 3rd Edn., Wiley, Oxford, UK, 2012. a, b