Nonlinear vortex solution for perturbations in the Earth's ionosphere

There is much observational evidence of different fine structures in the ionosphere and magnetosphere of the Earth. Such structures are created and evolve as a perturbation of the ionosphere's parameters. Instead of dealing with a number of linear waves, we propose to investigate and follow up the perturbations in the ionosphere by dynamics of soliton structure. Apart from the fact that this is a more accurate solution, the advantage of soliton solution is its localization in space and time as a consequence of the balance between nonlinearity and dispersion. The existence of such a structure is driven by the properties of the medium. We derive the necessary condition for having a nonlinear soliton wave, taking the vortex shape as a description of the ionosphere parameter perturbation. We employ a magnetohydrodynamical description for the ionosphere in plane geometry, including rotational effects, magnetic field effects via ponderomotive force, and pressure and gravitational potential effects, treating the problem self-consistently and nonlinearly. In addition, we consider compressible perturbation. As a result, we have found that Coriolis force and magnetic force on the one hand and pressure and gravity on the other hand determine dispersive properties. Dispersion at higher latitudes is mainly driven by rotation, while near the Equator, within the E and F layers of the ionosphere, the magnetic field modifies the soliton solution. Also, a very general description of the ionosphere results in the conclusion that the unperturbed thickness of the ionosphere layer cannot be taken as an ad hoc assumption: it is rather a consequence of equilibrium property, which is shown in this calculation.

1 Introduction

The structure of the Earth's ionosphere depends on its distance from the Earth's surface, involving different sources of disturbance in the basic parameters within it. These sources could be the subject of events in Earth, atmosphere, Sun, and γ-ray bursts (GRB) from deep space. Observation evidence of large-scale ionosphere structures is important as interpretation of the low-frequency perturbations of the ionosphere response to mentioned disturbance sources. That interpretation is an important research task, since the studies of perturbations induced in the ionosphere can be used in different fields related to human life, for example, prediction of natural disasters (atmospheric storms, volcano eruptions, earthquakes) or problems in satellite and electrical device operations.

Correlation between perturbation of the ionosphere parameters and atmospheric gravity waves generated by tsunamis was investigated in the beginning by Hines (1972) and Peltier and Hines (1976). Then, after the observational techniques were developed, research was spread to make an effort in establishing possible correlations in the detection of ionospheric effects with the earthquake event (Sobolev and Husamiddinov, 1985; Lyperovskaya et al., 2007; Pulinets, 2004). It was suggested by Arai et al. (2011) that it may be possible to indicate tsunami generation by monitoring acoustic-gravity waves in the ionosphere accompanied by undersea seismic disturbances. On the other hand, the earthquake precursor could be related to detection of ionosphere disturbances, observing the formation of ionospheric plasma concentration irregularities (Davies and Baker, 1965). The reason for the possible direct coupling of the processes in the deep earth layers and the ionosphere could be eventual transfer of a positive electric charge created by compression in rocks to the layers of the ionosphere (Freund et al., 2006). Apart from the above-mentioned ionospheric perturbation coming from the Earth's surface, there are a number of them caused by atmosphere or solar activity. There are several studies on the tropical depression influence on the ionosphere indicating electrical and electromagnetic effects. One direction of this research is investigation of the sudden disturbances in the low ionosphere which result in changes in radio signals (very low/low frequency (VLF/LF)) that are related to the short-term variations caused by lightning (Price et al., 2007). In this field, the great advance has been achieved using Global Positioning System (GPS) technology (Erickson et al., 2001) for monitoring ionospheric disturbances during solar flares (Afraimovich, 2000), but also by developing different simulations of the flare effects of the ionosphere (Huba et al., 2005; Meier et al., 2002). As far as ionosphere perturbations caused by GRB are concerned, there are few observational techniques to observe cosmic effects (Nina et al., 2005; Inan et al., 2007).

However, either of these phenomena has an influence on the basic ionosphere parameters, such as ion/electron density, electromagnetic field, pressure, and consequently neutral density. The problem with the detection of any mentioned parameter is in fact that it is difficult to filter out the origin of the perturbation since the amplitudes of the ionospheric anomalies are usually small. Instead of electromagnetic wave propagation, linear wave theory gives the opportunity to identify and detect frequencies of possible waves propagating within the ionosphere (gravity and acoustic modes), but the linearization procedure mimics the importance of nonlinear effects for the wave dynamics.

The aim of this paper is to describe perturbation in the ionosphere using a compressible fluid model with pressure, rotation, magnetic field, and scalar gravitational potential, involving nonlinear terms that are neglected in the linear approach. As a result, we obtain conditions for stable vortical structure formation. Simple monitoring of these structures gives an opportunity for fast prediction and reaction of mentioned events that could have an influence on humans.

Apart from these advantages, a number of solitary structures are directly observed as elements of plasma motion in the ionosphere and magnetosphere (Hallinan and Davis, 1970), and especially electron and ion density structures in the equatorial ionosphere (Lin et al., 2007; Huang et al., 2009).

Also, there is a number of simulations that have investigated different processes within the ionosphere that are possible to interpret by the nonlinear solitary solution, e.g., Maruyama et al. (2016), which discusses the density peak structure. As far as the experimental confirmation of the rotation importance for soliton creation is concerned, we recommend the work of van Hejist and Kloosterziel (1998).

2 Ionosphere model: basic equations and approximations

2.1 Basic equations

An analytical solution of the set of nonlinear partial differential equations, if possible, would give better insight into different processes that are responsible for the creation and distortion of such structures by deriving and investigating conditions for their existence. Although there are plenty of papers considering similar topics (Kaladze, 1998; Kaladze et al., 2004; Khantadze et al., 2009), all of them have used an assumption that is a consequence of general gravitational potential action.

In this paper, we use the general scalar gravitational potential, together with Poisson's equation, instead of a stream function or shallow water assumption, in order to derive conditions for ionosphere perturbation to take the shape of the soliton vortex. The condition for the soliton existence and shape within the ionosphere at low latitudes, close to the Equator, is analyzed in detail.

We assume the ionosphere to be a fluid consisting of neutral and charged particles, with z as the coordinate measuring the distance from the Earth's surface to the two-dimensional plane surface in the ionosphere. Since the ionosphere fluid is ionized with the ionization degree depending on the distance from the Earth's surface, three layers D, E, and F are defined, where each of them contains charged particles (electrons and ions) and neutrals. The neutral gas is strongly influenced, via the collisional coupling with low-density ions and electrons, by an electromagnetic force, so that in the momentum equation for the neutral gas there exist, apart from Coriolis force, pressure and gravitation and ion-neutral and electron-neutral collisional drag forces, via the electromagnetic force. We have neglected the inclination of the geomagnetic and Earth's North Pole of 11⁰ just for simplicity, with no loss of generality.

As far as the gravitational force is concerned, the ionosphere is influenced by the Earth's gravitation in the vertical direction but, for the first time here, we add Poisson's equation for gravitational potential of the neutral gas, relevant for this geometry, in contrast to the usual approach based on the assumption of shallow water theory (Kaladze et al., 2004) or using a stream function description for incompressible fluid (Kaladze, 1998). We use a finite thickness approximation in order to estimate gravity influence on the ionospheric gas dynamics, not only in the vertical direction, but also mainly in the horizontal plane, relevant for vortex soliton formation (Vukcevic, 2019). Assumption of shallow water theory is just a consequence of the general Poisson equation, approximated in the horizontal plane, and it will be shown in this work. The closed system of equations describing the ionosphere reads as follows. The continuity equation for compressible fluid is

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\partial \mathit{\rho }}{\partial t}}+\mathrm{\nabla }\cdot \left(\mathit{\rho }\mathit{v}\right)=\mathrm{0},\end{array}$$

where ρ is neutral gas volume density, and v is neutral gas velocity; the equation of motion is

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\partial \mathit{v}}{\partial t}}+(\mathit{v}\cdot \mathrm{\nabla })\mathit{v}+\mathrm{2}(\mathbf{\Omega }\times \mathit{v})+{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}(\mathit{j}\times {\mathit{B}}_{\mathrm{0}})=\mathrm{\nabla }\mathrm{\Phi }+{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}\mathrm{\nabla }P,\end{array}$$

where Ω is the angular velocity of the Earth's rotation, j is the conduction current density, B₀ is the geomagnetic field, and Φ and P are scalar three-dimensional gravitational potential and pressure, respectively; Poisson's equation is

$$\begin{array}{}\text{(3)}& \mathrm{\Delta }\mathrm{\Phi }=-\mathrm{4}\mathit{\pi }G\mathit{\rho },\end{array}$$

with ρ and Φ previously defined, and the current equation

$$\begin{array}{}\text{(4)}& \mathit{j}={\mathit{\sigma }}_E\mathit{E}+{\displaystyle \frac{{\mathit{\sigma }}_E}{B_{\mathrm{0}}}}({\mathit{B}}_{\mathrm{0}}\times \mathit{E})=en(\mathit{v}-{\mathit{v}}_{\mathrm{e}}),\end{array}$$

where E is the dynamo electric field, σ_E is the conductivity tensor, n is the number density of charged particles, e is the electron charge, and v_e is the electron velocity.

The electric dynamo field equation is

$$\begin{array}{}\text{(5)}& \mathit{E}=(\mathit{v}\times {\mathit{B}}_{\mathrm{0}}).\end{array}$$

Here we use the following plasma condition in the ionosphere: ions are considered unmagnetized, so that v_i=v, ion velocity across the magnetic field is equivalent to gas velocity, and ions are dragged by neutral gas motion completely, while the electrons are magnetized and frozen in the external magnetic field, so that ${\mathit{v}}_{\mathrm{e}}=(\mathit{E}\times {\mathit{B}}_{\mathrm{0}})/B_{\mathrm{0}}^{\mathrm{2}}$ (Kaladze et al., 2004). Details of derivation of Eq. (2) and involvement of the electric field are given in Appendix A. Equation (2) is the same as Eq. (A5). In the equation of motion, viscous effects are neglected due to high Hartmann number for typical ionosphere parameters ($H{a}^{\mathrm{2}}=\frac{\mathit{\sigma }{B}_{\mathrm{0}}^{\mathrm{2}}{L}^{\mathrm{2}}}{\mathit{\eta }\mathit{\rho }}\sim {\mathrm{10}}^{\mathrm{5}}$), where η is kinematic viscosity $\cong {\mathrm{10}}^{-\mathrm{5}}$ kg m⁻¹ s⁻¹ (Kaladze et al., 2004).

In this research, scalar gravitational potential is related to neutral gas at the z=z₀ distance from the Earth's surface, where it is defined by the Earth's gravitation only in the z direction but remains the two-dimensional, horizontal component defined by gas in the vicinity of a fixed distance from the Earth. Assumption of the stratified stable ionospheric layer involves the Brunt–Väisälä frequency which is fast compared to large-scale horizontal motion that will be considered here using drift approximation. We will show that the general scalar gravitational potential is equivalent to the effective height of shallow water theory within approximation of Poisson's equation, as was proposed by Vukcevic (2019). Within that approximation, scalar potential is evaluated as two-dimensional denoted by ϕ, while volume density is evaluated by surface density σ and pressure as two-dimensional pressure denoted by p. Details of Poisson's equation approximation are given in Appendix B.

2.2 Drift approximation

In order to qualitatively estimate contributions of rotation, gravity, pressure, and magnetic effects, we will employ drift approximation, and at first, we may assume a pseudo-three-dimensional case such that

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\partial \mathit{v}}{\partial z}}=\mathit{ϵ}({\mathrm{\nabla }}_{⟂}\cdot v_{⟂}),\end{array}$$

which is in good agreement with experimental data (Dokuchaev, 1959).

Here, the subscript ⟂ indicates the components of the variables within the ionosphere plane surface, and ϵ is a small parameter on the order of either $(\mathrm{2}b\mathrm{\Omega }{)}^{-\mathrm{1}}\frac{d}{\mathrm{d}t}$ or $\left(\mathrm{2}b\right(\mathrm{\Omega }+en{B}_{\mathrm{0}}/\mathit{\rho }{)}^{-\mathrm{1}}\frac{d}{\mathrm{d}t}$, where b is a corrective factor denoting sin φ, and φ is latitude measured from the Equator.

The last assumption is consistent with the condition of existence of a drift wave and physically means that fluid inertia in the direction of the ambient rotation or/and magnetic field is negligible, or equivalently, that ionospheric motions in the vertical direction, defined by z, are much less than those in the horizontal one defined by x and y (Pudovkin, 1974).

Within a local Cartesian system defined by e_x, e_y, and e_z as the east, north, and up directions, respectively (see Fig. 1), Earth's angular velocity has the following components: $\mathrm{\Omega }=\mathrm{\Omega }(\mathrm{0},\sqrt{\mathrm{1}-b^{\mathrm{2}}}\mathrm{\Omega },b\mathrm{\Omega })$, where the Equator is defined by b=0, while the pole is defined by b=1. Consequently, the geomagnetic field, assumed to be a magnetic dipole, has components as $B_{\mathrm{0}}=B_{\mathrm{0}}(\mathrm{0},\sqrt{\mathrm{1}-b^{\mathrm{2}}}{B}_{\mathrm{0}},-\mathrm{2}b{B}_{\mathrm{0}})$.

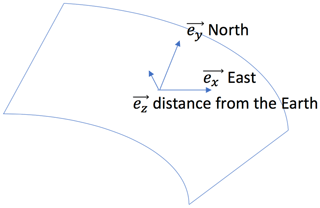
Figure 1 Local coordinate system. In the horizontal plane are defined two axes by unit vectors: e_x oriented to the east and e_y oriented to the north. The vertical axis to the horizontal plane is defined by unit vector e_z; along this axis is defined the distance of the horizontal plane from the Earth's surface.

Making a vector product of the equation of motion, Eq. (2), and e_z, we obtain

$$\begin{array}{}\text{(7)}& \begin{array}{rl}\left({\displaystyle \frac{\partial \mathit{v}}{\partial t}}+(\mathit{v}\cdot \mathrm{\nabla })\mathit{v}\right)& \times {\mathit{e}}_z+\mathrm{2}(\mathbf{\Omega }\times \mathit{v})\times {\mathit{e}}_z+{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}(\mathit{j}\times {\mathit{B}}_{\mathrm{0}})\\ & \times {\mathit{e}}_z=(\mathrm{\nabla }\mathit{\varphi }+\mathrm{\nabla }p)\times {\mathit{e}}_z.\end{array}\end{array}$$

Let us now investigate in detail the second and third terms on the left-hand side of Eq. (7), denoting them as $f_R=\mathrm{2}(\mathbf{\Omega }\times \mathit{v})\times {\mathit{e}}_z$ and $f_H=\frac{\mathrm{1}}{\mathit{\rho }}(\mathit{j}\times {\mathit{B}}_{\mathrm{0}})\times {\mathit{e}}_z$. f represents the coupled rotational and magnetic field contribution. Writing them as

$$\begin{array}{}\text{(8)}& \begin{array}{rl}f& =f_R+f_H=\mathrm{2}b\left(\mathrm{\Omega }+{\displaystyle \frac{en{B}_{\mathrm{0}}}{\mathit{\rho }}}\right)\left[v_x,v_y,\mathrm{0})\right]\\ & -{\displaystyle \frac{\mathrm{2}enb{B}_{\mathrm{0}}}{\mathit{\rho }}}\left[\mathrm{5}(\mathrm{1}-b^{\mathrm{2}})v_x,(\mathrm{1}-\mathrm{2}{b}^{\mathrm{2}})v_y,\mathrm{0})\right],\end{array}\end{array}$$

we are able to derive the relevant parameter necessary for applying drift approximation. In order to compare these two terms in the last expression, rotation and magnetic field contribution, we next consider two extreme cases, pole and Equator.

Case (a): in the extreme case b=1, at the pole, Eq. (8) is simplified and reads as

$$\begin{array}{}\text{(9)}& f=\mathrm{2}\left(\mathrm{\Omega }-{\displaystyle \frac{en{B}_{\mathrm{0}}}{\mathit{\rho }}}\right)\left[(v_x,v_y,\mathrm{0})\right].\end{array}$$

This result is similar to the result obtained by Kaladze (1998), but with different approaches of the stream function for incompressible fluid, with no gravitation involved, for motions far from the Equator. That approach used, the so-called β plane approximation, breaks down at polar latitudes.

For very high latitudes, close to the pole, b→1, Eq. (8) becomes

$$\begin{array}{}\text{(10)}& f=f(x,y)=\mathrm{2}\mathrm{\Omega }\left[(v_x,(\mathrm{1}-{\displaystyle \frac{\mathrm{1.5}en{B}_{\mathrm{0}}}{\mathrm{\Omega }\mathit{\rho }}})v_y,\mathrm{0})\right].\end{array}$$

The ratio of the magnetic field and rotation defines the y component of the velocity, conditioning the shape of the structure. We will discuss this result and implications for the solution in Sect. 4.

Case (b): in the extreme case, at the Equator plane b=0, structure formation is not possible since both terms in Eq. (8) are equal to 0. That result is the same as that obtained in a number of papers considering the same problem (Kaladze, 1998). Let us investigate the case for low latitudes, close to the Equator, b→0, since there are plenty of observed structures within that region that have no explanation at all. Equation (8) for latitudes θ≳6⁰ becomes

$$\begin{array}{}\text{(11)}& f=f(x,y)=\mathrm{0.2}\mathrm{\Omega }\left[\left(\mathrm{1}-{\displaystyle \frac{\mathrm{5}en{B}_{\mathrm{0}}}{\mathrm{\Omega }\mathit{\rho }}}\right)v_x,v_y,\mathrm{0}\right].\end{array}$$

For such a case, the existence of the ambient magnetic field would modify the solution, depending on the ratio of the magnetic field and rotation contribution.

3 Nonlinear equation

Applying drift approximation and using Poisson's equation approximated by two-dimensional functions for density and scalar potential in order to derive the nonlinear equation, the set of Eqs. (1)–(3) will transform to

$$\begin{array}{}\text{(12)}& \left\{\begin{array}{c}\frac{\partial }{\partial t}\mathit{\sigma }+\mathit{\{}\mathit{\varphi },({\mathit{\sigma }}_{\mathrm{0}}+\mathit{\sigma }\left)\mathit{\right\}}=\mathrm{0},\\ \mathit{\sigma }=-A{\mathrm{\nabla }}_{⟂}^{\mathrm{2}}\mathit{\varphi }+B\mathit{\varphi }.\end{array}\right.\end{array}$$

Here the drift velocity is defined by

$$\begin{array}{}\text{(13)}& {\mathit{v}}_{\mathrm{d}}=\mathrm{\nabla }\mathit{\varphi }\times {\mathit{e}}_z,\end{array}$$

while v_i is the inertial velocity, and it depends on the velocity given by Eq. (7). The three-dimensional Poisson equation is evaluated in two-dimensional plane geometry, in the neighborhood of z=z₀ as proposed by Vukcevic (2019), involving the thickness of the plain via functions A and B.

Case (a): at the pole, inertial velocity is defined by

$$\begin{array}{}\text{(14)}& {\mathit{v}}_{\mathrm{i}}=\left({\displaystyle \frac{\partial }{\partial t}}+\mathit{v}\cdot \mathrm{\nabla }\right)\mathit{v}+\left(\mathrm{2}\mathrm{\Omega }+{\displaystyle \frac{en{B}_{\mathrm{0}}}{\mathit{\rho }}}\right)\mathit{v}.\end{array}$$

In the limit of low-frequency perturbations (which is equivalent to a long-period perturbation; according to observations the solitary structure lasts from a few hours up to a few days, in size from a few tens up to a few kilometers Lin et al., 2007; Anderson et al., 2002) we can omit inertial terms in the further calculations, so that velocity is approximated by v_d. It will result in the normalization of the variables by the factor 2Ω+H, where $H=\frac{en{B}_{\mathrm{0}}}{\mathit{\rho }}$. After this assumption all variables will be evaluated within the (x,y) plain, and Poisson's equation is approximated with the finite thickness evaluation in the vicinity of z=z₀, which is at a certain distance from the Earth's surface (for details, see Appendix B).

Consequently, we look for the stationary waves which are described by Eq. (12) assuming that $\mathit{\varphi }=\mathit{\varphi }(y-ut,x),$ where u is a constant parameter meaning the wave velocity along y. x and y are the local coordinates previously defined. Then, Eq. (12) takes the form

$$\begin{array}{}\text{(15)}& \begin{array}{rl}-\mathrm{2}u& (\mathrm{\Omega }+H){\displaystyle \frac{\partial }{\partial y}}(B\mathit{\varphi }-A{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi })-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{B}^{\prime }{\displaystyle \frac{\partial }{\partial y}}{\mathit{\varphi }}^{\mathrm{2}}+A(\mathrm{\nabla }\mathit{\varphi }\times \mathrm{\nabla }{)}_z\\ & {\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }++({\mathit{\varphi }}_{\mathrm{0}}^{\prime }B-{\mathit{\sigma }}_{\mathrm{0}}^{\prime }){\displaystyle \frac{\partial }{\partial y}}\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}}^{\prime }A{\displaystyle \frac{\partial }{\partial y}}{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }=\mathrm{0},\end{array}\end{array}$$

where ^′ denotes the derivative with respect to x. The last equation corresponds to Eq. (B13) in Appendix B, if divided by 2(Ω+H), which represents f in this case.

If the latitudes are close to the pole, due to a change in the inertial velocity, the shape of the solution will be changed because the y component of the velocity depends on the ratio of magnetic and rotation values. The shape of the solution will be discussed and given in the next section.

Case (b): for latitudes close to the Equator, the second term in the expression for inertial velocity is conditioned by values of magnetic field influence and Coriolis force influence (see Eqs. 8 and 11). Consequently, it influences the normalization value for the velocity as well as the shape of the soliton. If the magnetic field strength is small compared to the rotation, the nonlinear equation is similar to the previous equation and reads as

$$\begin{array}{}\text{(16)}& \begin{array}{rl}-\mathrm{0.2}uf& {\displaystyle \frac{\partial }{\partial y}}(B\mathit{\varphi }-A{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi })-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{B}^{\prime }{\displaystyle \frac{\partial }{\partial y}}{\mathit{\varphi }}^{\mathrm{2}}+A(\mathrm{\nabla }\mathit{\varphi }\times \mathrm{\nabla }{)}_z\\ & {\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }++({\mathit{\varphi }}_{\mathrm{0}}^{\prime }B-{\mathit{\sigma }}_{\mathrm{0}}^{\prime }){\displaystyle \frac{\partial }{\partial y}}\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}}^{\prime }A{\displaystyle \frac{\partial }{\partial y}}{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }=\mathrm{0}.\end{array}\end{array}$$

Consequently, the soliton shape is symmetric and the amplitude of the soliton is changed. In the case where the magnetic parameter H is on the order of 0.2Ω, the solution will be elongated along the y axis, while if H⩾0.4Ω, the soliton will change its moving direction and one can expect a structure elongated along the x axis. This is because the normalization value has different velocity components, and these two cases will be estimated and discussed in the next section.

Here, we underline the difference between the Rossby waves derived using the so-called geostrophic approximation for the number of fluids, planetary atmospheres, or plasma drift waves (Sommeria et al., 1988; Marcus, 1989; Hasegawa et al., 1979) and the nonlinear soliton wave solution discussed by Petviashvili (1983) and Vukcevic (2019). The first reason for the different structure comes from different dispersion relations derived in the linearized problem. In our case it reads as

$$\begin{array}{}\text{(17)}& \mathit{\omega }={\mathit{v}}_{\mathrm{0}}\cdot \mathit{k}+{\displaystyle \frac{\mathit{k}\cdot ({\mathit{e}}_z\times \mathbf{\nabla }{\mathit{\sigma }}_{\mathrm{0}})}{(\mathrm{1}-(A/B\left)k^{\mathrm{2}}\right)}},\end{array}$$

while in the case for Rossby waves it is

$$\begin{array}{}\text{(18)}& \mathit{\omega }={\displaystyle \frac{\mathit{k}\cdot ({\mathit{e}}_z\times \mathbf{\nabla }{\mathit{\sigma }}_{\mathrm{0}})}{(\mathrm{1}-(A/B\left)k^{\mathrm{2}}\right)}}.\end{array}$$

Consequently, the nonlinear equation describing Rossby waves contains the nonlinear term which is of the vector type, connected with the term [∇ϕ×∇]_z (Korchagin and Petviashvili, 1985; Korchagin et al., 1987; Fridman and Khoruzhii, 1999). In our case, the crucial term is the one connected with term B^′, which is related to the equilibrium property of the fluid, namely, surface density that is x dependent and thickness of the layer.

4 Results: soliton vortex solution

In this section it will be shown how the solution of the nonlinear equation derived in the previous section depends on the thickness of the layer. Nonlinear Eqs. (15) and (16) are similar, and we look for the solution of either of them in the form

$$\begin{array}{}\text{(19)}& {\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }=\mathit{\lambda }\left(x\right)\mathit{\varphi }+\mathit{\nu }\left(x\right){\mathit{\varphi }}^{\mathrm{2}},\end{array}$$

where λ and ν are functions of x caused by both an inhomogeneity of the equilibrium functions and the thickness of the plain surface that we need to find out. Functions λ and ν read as follows:

$$\begin{array}{}\text{(20)}& {\displaystyle }\mathit{\lambda }\left(x\right)={\displaystyle \frac{\mathrm{1}}{A}}\left(B-{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{0}}^{\prime }}{u}}\right),\text{(21)}& {\displaystyle }\mathit{\nu }\left(x\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}u}}\left(\mathit{\lambda }{A}^{\prime }+{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{0}}^{\prime \prime }}{u}}\right),\end{array}$$

where ^′′ represents second derivative with respect to x.

Even for constant B ($B^{\prime }=\mathrm{0}$), the nonlinear term ϕ² remains due to the gradient of factor A and the extremum of the function σ₀, which is the equilibrium property of the surface density. It is an important result since it suggests that the equilibrium thickness of the layer cannot be taken as constant; thickness is related either to the gradient of A or to the surface density function extremum (see Eq. 21).

Then, the stable solution of Eq. (15) or (16) reads as

$$\begin{array}{}\text{(22)}& \mathit{\varphi }={\displaystyle \frac{\mathrm{2}\mathit{\lambda }}{\mathit{\nu }}}F\left(R\right),\end{array}$$

where $R=\sqrt{\mathit{\lambda }}r$ is the dimensionless radius in the moving frame, and F is the solution of the equation

$$\begin{array}{}\text{(23)}& {\displaystyle \frac{\mathrm{1}}{R}}{\displaystyle \frac{\partial }{\partial R}}R{\displaystyle \frac{\partial f}{\partial R}}=F-F^{\mathrm{2}}.\end{array}$$

The approximate solution of Eq. (23) is (Zakharov and Kuznetsov, 1974)

$$\begin{array}{}\text{(24)}& F=\mathrm{2.4}{\left(\cosh \left({\displaystyle \frac{\mathrm{3}}{\mathrm{4}}}R\right)\right)}^{-\frac{\mathrm{4}}{\mathrm{3}}},\end{array}$$

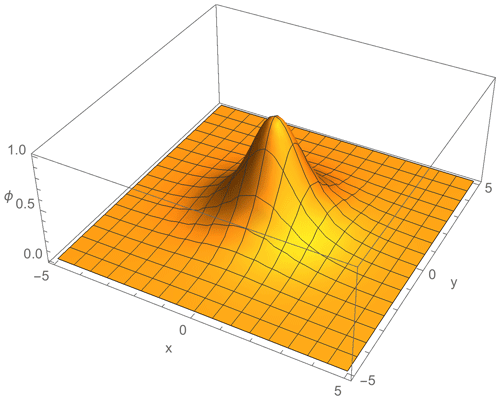
which means that the potential has a solution taking the form of a steady solitary vortex shown in Fig. 2, where R represents the dimensionless distance to the center of the vortex. The vortex travels along the y coordinate, northward in our description, with constant velocity u.

Let us now investigate the cases when the normalization value is not symmetric. Close to the pole, if the magnetic parameter H is on the order of Ω, one can expect a symmetric solution if the H<Ωv_y component is smaller than v_x (see Eq. 10) and the solution is changed and reads as

$$\begin{array}{}\text{(25)}& F=\cosh {\left({\displaystyle \frac{\mathrm{3}}{\mathrm{4}}}R(\mathrm{1}+f(x\left)\mathrm{\Lambda }\right)\right)}^{-\frac{\mathrm{4}}{\mathrm{3}}}.\end{array}$$

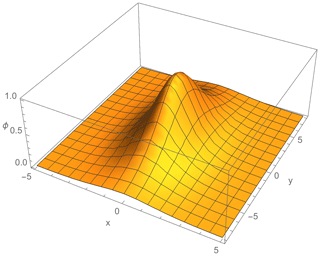
The solution of scalar potential approximated by Eq. (25) represents the asymmetric soliton vorticity shape of scalar potential shown in Fig. 4.

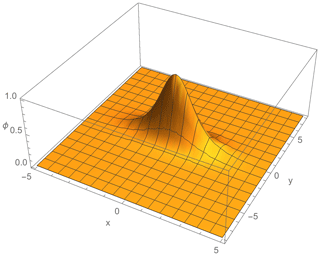
Related to these two types of potential given by Eqs. (24) and (25), there are three different possibilities in the area close to the Equator: H≪Ω solution is symmetric with the amplitude higher than in the symmetric case close to the pole; H∼0.2Ω solution will be elongated along the y axis and is shown in Fig. 3; if H⩾0.4Ω, the soliton will be symmetric, but it will change the moving direction, since the v_x component has the opposite sign.

Figure 2 Potential derived in Eq. (22). Horizontal axes represent the x and y coordinates, while the vertical axis represents non-dimensional potential.

Figure 3 Shape of the potential in the Equator vicinity elongated along the y axis.

Figure 4 Shape of the potential close to the pole elongated along the x axis.

5 Discussion

There is very clear evidence of the ion density depletion in Fig. 1 of Huang et al. (2009), which can be explained as a consequence of the particles trapped by medium nonlinear scalar potential that will be derived in this paper. One should not expect to observe within the ionosphere vortices as is common in the atmosphere, but any regular depletion or enhancement of density can be explained by the mechanism that we propose here. Although the ionosphere is very complex and dynamical, there are a number of approximations used in previous theoretical and numerical research that worked well compared with observed parameters. For example, there is an interaction between sheared zonal flow within the ionosphere and Rossby solitons created in the atmosphere of the Earth, making a turbulent stage via accumulation of the flow energy into vortical structures. Here, we propose the existence of the magnetized stable vortices created in the ionosphere that could be used as a transient stage of a highly turbulent medium. Recent explanations of the zonal flow creation have been innhomogenous heating of the atmospheric and ionospheric layers by solar radiation, but previously, there was a number of studies investigating the creation of sheared zonal flow as a consequence of nonlinear mechanism excitation by planetary waves or tides. As suggested by Immel et al. (2006), it is not unexpected that tides are able to modulate the dynamo electric fields within the E and F layers. It would be of great interest to investigate how this interaction influences the creation of magnetized solitons derived in this research, since the model of the ionosphere includes conductive fluid with coupled strong interaction of charged particles via Lorentz force. Since the ionosphere represents a slightly ionized gas, so that neutral particles are the dominant components, it is expected that self-gravity in the horizontal plane would play a significant role in the structure formation. It is more realistic to use scalar self-gravity potential accompanied by Poisson's equation and to treat the fluid as compressible, instead of an incompressible fluid description using the stream function. According to Haldoupis and Pancheva (2002), the conviction of the horizontal plasma transport as being unimportant in the E layers (since the scales involved are much larger than the vertical ones) had to be reconsidered due to new evidence, by Tsunoda et al. (1998), which suggested a link between E layers and planetary waves. Planetary waves are global-scale oscillations in neutral wind, pressure, and density, which prevail and propagate zonally in the mesosphere and lower thermosphere and have periods mostly near 2, 5, 10, and 16 d (Forbs an Leveroni, 1992). It has been shown that horizontal formations capture medium particles and transfer these particles in their movement. Here, we have shown that, as an analogy of planetary waves, there are nonlinear wave formations in the ionosphere that could be used in order to follow the dynamics of the ionosphere in an easier manner. Therefore, the vortices can considerably contribute to the convective intermixing of a medium.

In this work we have found a soliton solution in a few different cases, on the pole, close to the pole, and close to the Equator of the ionosphere. We have confirmed a few results obtained by using different approaches, with an emphasis on the cause of the obtained phenomena. It is shown that the surface mass density disturbance in the shallow water theory approach is just a consequence of scalar gravitational potential action via Poisson's equation used in this work. Also, we have proved that the thickness of the layer can be uniform (see Eq. 21, even if $A^{\prime }=\mathrm{0}$ remains the term ${\mathit{\sigma }}_{\mathrm{0}}^{\prime \prime }$), but the soliton existence is driven by the inhomogeneity of the equilibrium mass surface density. The advantage of such a solution in studying ionospheric disturbances of any kind is the fact that the amplitude and velocity of the soliton are very sensitive to ionospheric parameters (density of charged particles, and consequently of pressure, gravity, magnetic field, and rotation velocity values), which means that once the balance between all of them fails, a distortion of the structure will result. Thus, it is very easy to predict consequences caused by maximum or minimum neutral, so that electron concentration, just by simple monitoring of the structure dynamics within the ionosphere region. This is in contrast to the investigation of the ionospheric anomaly influence by some other methods, involving very small amplitudes of either linearized periodic waves or electromagnetic waves that need to be filtered out in order to define the source, after a number of reflections by the ionosphere.

It is important to underline that the type of vortex, when it is symmetric, is defined by the extremum value of density inhomogeneity via the term in ν Eq. (21): cyclones by minimum, anticyclones by maximum. Also, if the potential is a bright soliton, consequently the density is represented by a dark one since particles are trapped by such potential, and vice versa; whenever the potential is a dark soliton, density will be enhanced, represented by a bright one. It is possible further to investigate more detailed conditions of the solitary structure for different ionosphere layers.

• Ionosphere D layer. Within this region, located 50–100 km from the Earth's surface, we can assume that the contribution of charged particles can be neglected, so the ponderomotive force effects are small compared to the Coriolis force effects (Gershman, 1974). This means that it is likely to expect a solitary structure for small latitudes, close to the Equator, elongated along the y coordinate, while for high latitudes and at the pole, the soliton is symmetric, the size of the soliton will depend on the density gradient, and its velocity is normalized by $f=f_R=\mathrm{\Omega }$.

• Ionosphere E layer. This layer is located 100–150 km from the Earth's surface, and one can expect the creation of a soliton at all latitudes higher than 6⁰, since the ponderomotive force is on the order of the Coriolis one. In this case, soliton velocity is defined by $f=\mathrm{2}(\mathrm{\Omega }+H)$ at the pole and for latitudes close to the pole. Since the value H has the opposite sign to Ω, the cancelation of the vortex structure is possible when these two terms are on the same order or it is possible to change the moving direction of the soliton structure. Next, the size of the soliton is defined by $R=\sqrt{\mathit{\lambda }}r$ and, consequently, by soliton velocity u, which for this case is defined by 2(Ω+H); one expects the size to increase compared with the same case for the D layer. As far as the low-latitude case is concerned, the latitudes close to the Equator and the size and velocity of the soliton are dependent on the value H compared to Ω, and even more, the soliton is not symmetric but rather extended along the y axes, since $f=f(x,y)$.

• Ionosphere F layer. The ionospheric F layer is for heights 150–400 km from the Earth's surface. In this case, for all latitudes soliton structure is mainly defined by the value 0.2H. At the pole, the soliton is symmetric and velocity is defined by f=2H, while close to the Equator one can expect a soliton elongated along the x axis but moving in the opposite direction compared to the E and D layers, because $f=f(x,y)=f_H$.

Nonlinear effects are extremely important in wave dynamics whenever they are comparable with dispersive properties of the medium that are defined by gradients of pressure and gravity potential, rotation, and magnetic force. One very good example of the balance between nonlinear and dispersive effects is a tsunami, a surface gravity wave that can propagate for a long time with large constant velocity and large amplitude, with no distortion or dissipative effects, as long as the conditions of balance are satisfied, so that such a solution is stable in space and time, propagating with the constant velocity and amplitude. The fact that this solution is very sensitive to even very small changes in any parameter makes instant detection possible of such a change by distortion of the structure.

6 Conclusions

We have studied nonlinear dynamics of fine structures in the Earth's ionosphere within drift approximation, with primary emphasis on the necessary conditions for vortex soliton creation. We have included all relevant physical forces in the model, keeping nonlinear terms, and applied them at the Equator of the ionosphere. A series of direct observations of such soliton structures are carried out either from the Earth's surface or onboard the satellites. We have summarized all possible soliton structure formations at different latitudes, as well as at different ionospheric layers. The soliton size and velocity are constant but defined by different values of ionospheric parameters. From our investigation of the soliton solution in the conditions of the Earth's ionosphere we can outline the following conclusions.

• A stable localized solution of a partial nonlinear differential equation is possible under the balance between nonlinear terms and dispersion, while dispersion is caused by the Coriolis force and magnetic field force on the one hand and gravity and pressure on the other hand. A necessary condition for its existence is either nonuniform thickness of the layer or the existence of an extremum of the equilibrium mass surface density function.

• The amplitude and velocity of the soliton are very sensitive to ionospheric parameters (density of neutrals, charged particles, and consequently of pressure, gravity, magnetic field, and rotation velocity values), which means that once the balance between all of them fails, a distortion of the structure will result.

• In general, a nonlinear equation that has a soliton solution is possible at all latitudes higher than 6⁰, but the physical processes responsible for it are different. Close to the Equator, the presence of a magnetic field is crucial since effects of rotation are very small, while on the pole it is always a combination of the rotation and magnetic effects, with the possibility for the soliton to vanish due to opposite signs of these two effects.

• Soliton existence is a direct consequence of the equilibrium condition on the layer thickness. The equilibrium must be defined either by the extremum of the surface density function or by parameter A.

• In the ionosphere D layer it is likely to expect a solitary structure close to the Equator, but if it is created the soliton is elongated along the y coordinate. Close to the pole, the size of the soliton will depend on the density gradient, and its velocity is normalized by Ω.

• The ionosphere E layer is characterized by two types of solitons: close to the pole the soliton vortex is symmetric, with sizes larger than in the D layer with the possibility of vanishing, and close to the Equator the existence is caused by the magnetic field presence, and the soliton is elongated along the y axis.

• The opposite situation is within the ionosphere F layer where at the pole there exists a symmetric soliton larger then in the ionosphere D layer at the pole, while close to the Equator there exists an extended soliton structure.

Finally, we hope that this model will be used in explanations of the ionosphere structures as well as in testing the physics background of complex ionosphere simulations. This model can be used not only to model the ionosphere structure, but also for different astrophysical systems, e.g., accretion disks, where the thickness effects could be very important. Therefore, finite thickness effects should be taken into account. However, this approach can be improved by trying to find out the correlation between soliton structure dynamics and other methods used to identify the ionospheric anomalies. Also, it would be of great importance to investigate the stability of the soliton structure as the subject of small disturbances and apply it to the study of the interaction between the solitons within different ionospheric layers. All of these mentioned issues will be considered in further research.

Appendix A: Derivation of the momentum equation for the neutral gas influenced by low-density ions and electrons

As is mentioned in Sect. 2, the neutral gas is strongly influenced by a strong electric field as the interaction of coupled charged particles, electrons and ions. That interaction enters in the neutral gas momentum equation via collisional drag forces of neutral particles and charged particles in the ionosphere. So that, there are three coupled momentum equations

$$\begin{array}{}\text{(A1)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\partial \mathit{v}}{\partial t}}& +(\mathit{v}\cdot \mathrm{\nabla })\mathit{v}+\mathrm{2}(\mathbf{\Omega }\times \mathit{v})=\mathrm{\nabla }\mathrm{\Phi }+{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}\mathrm{\nabla }P+m_{\mathrm{i}}{n}_{\mathrm{i}}N\langle \mathrm{\Sigma }\mathit{\nu }{\rangle }_{\mathrm{in}}\\ & ({\mathit{v}}_{\mathrm{i}}-\mathit{v})+m_{\mathrm{e}}{n}_{\mathrm{e}}N\langle \mathrm{\Sigma }\mathit{\nu }{>}_{\mathrm{en}}({\mathit{v}}_{\mathrm{e}}-\mathit{v}),\end{array}\text{(A2)}& {\displaystyle }\begin{array}{rl}{m}_{\mathrm{i}}{n}_{\mathrm{i}}& {\displaystyle \frac{\partial {\mathit{v}}_{\mathrm{i}}}{\partial t}}=\mathrm{\nabla }{P}_{\mathrm{i}}+n_{\mathrm{i}}{e}_{\mathrm{i}}(\mathit{E}+{\mathit{v}}_{\mathrm{i}}\times \mathit{B})-m_{\mathrm{i}}{n}_{\mathrm{i}}N\\ & \langle \mathrm{\Sigma }\mathit{\nu }{\rangle }_{\mathrm{in}}({\mathit{v}}_{\mathrm{i}}-\mathit{v}),\end{array}\text{(A3)}& {\displaystyle }\begin{array}{rl}{m}_{\mathrm{e}}{n}_{\mathrm{e}}& {\displaystyle \frac{\partial {\mathit{v}}_{\mathrm{e}}}{\partial t}}=\mathrm{0}=\mathrm{\nabla }{P}_{\mathrm{e}}-n_{\mathrm{e}}e(\mathit{E}+{\mathit{v}}_{\mathrm{e}}\times \mathit{B})\\ & -m_{\mathrm{e}}{n}_{\mathrm{e}}N\langle \mathrm{\Sigma }\mathit{\nu }{\rangle }_{\mathrm{en}}({\mathit{v}}_{\mathrm{e}}-\mathit{v}).\end{array}\end{array}$$

In these three equations index i or e denotes ion and electron, respectively, while 〈Σν〉_in and 〈Σν〉_en are the collision cross sections for neutrals with charged particles. Consequently, collision frequencies are ν_i=N〈Σν〉_in and N〈Σν〉_en for the ions and electrons. Coriolis force for ions and electrons is negligible compared to the Lorentz force since ${\mathit{\nu }}_{\mathrm{e}}\sim {\mathrm{10}}^{\mathrm{6}}\mathrm{1}/s\gg {\mathit{\omega }}_{\mathrm{ci}}\sim \mathrm{2}\times {\mathrm{10}}^{\mathrm{2}}\mathrm{1}/s$ and ${\mathit{\nu }}_{\mathrm{i}}\sim {\mathrm{10}}^{\mathrm{3}}\mathrm{1}/s\ll {\mathit{\omega }}_{\mathrm{ce}}\sim \mathrm{6}\times {\mathrm{10}}^{\mathrm{6}}\mathrm{1}/s$; both are much higher than the horizontal component of Coriolis acceleration $f_{\mathrm{c}}\sim \mathrm{6}\times {\mathrm{10}}^{-\mathrm{5}}\mathrm{1}/s$ at the midlatitude for the E layer, where ${\mathit{\omega }}_{\mathrm{ci},\mathrm{e}}=eB/m_{\mathrm{i},\mathrm{e}}$ are the cyclotron frequencies for ions and electrons, respectively. From the same estimation it is obvious that ion frictional force is much higher than the electron one due to the mass ratio of electron and ion. Adding Eqs. (A2) and (A3), we obtain

$$\begin{array}{}\text{(A4)}& \begin{array}{rl}{m}_{\mathrm{i}}& n_{\mathrm{i}}{\displaystyle \frac{\partial {\mathit{v}}_{\mathrm{i}}}{\partial t}}=\mathrm{\nabla }(P_{\mathrm{i}}+P_{\mathrm{e}})+n_{\mathrm{e}}e({\mathit{v}}_{\mathrm{i}}-{\mathit{v}}_{\mathrm{e}})\times \mathit{B}-m_{\mathrm{i}}{n}_{\mathrm{i}}N\\ & \langle \mathrm{\Sigma }\mathit{\nu }{\rangle }_{\mathrm{in}}({\mathit{v}}_{\mathrm{i}}-\mathit{v})-m_{\mathrm{e}}{n}_{\mathrm{e}}N\langle \mathrm{\Sigma }\mathit{\nu }{\rangle }_{\mathrm{en}}({\mathit{v}}_{\mathrm{e}}-\mathit{v}),\end{array}\end{array}$$

where it has been used as a quasi-neutral condition $n_{\mathrm{i}}=n_{\mathrm{e}}=n$. Applying ${\mathit{v}}_{\mathrm{e}}=\mathit{E}\times \mathit{B}/B^{\mathrm{2}}$ from Eq. (A3) to Eq. (A4), neglecting higher-order drift contributions such as diamagnetic drift, and since v_i=v due to very rapid ion velocity evolvement, using $n_{\mathrm{e}}e(\mathit{v}-{\mathit{v}}_{\mathrm{e}})=\mathit{v}=\mathit{j}$, we substitute Eq. (A4) into Eq. (A1), and we finally obtain the momentum equation for neutral gas as follows:

$$\begin{array}{}\text{(A5)}& {\displaystyle \frac{\partial \mathit{v}}{\partial t}}+(\mathit{v}\cdot \mathrm{\nabla })\mathit{v}+\mathrm{2}(\mathbf{\Omega }\times \mathit{v})=\mathrm{\nabla }\mathrm{\Phi }+{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}\mathrm{\nabla }P+{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}(\mathit{j}\times \mathit{B}).\end{array}$$

In the last equation we have neglected ion and electron pressure compared with neutral gas pressure due to $P_{\mathrm{e},\mathrm{i}}/P\sim n/N\ll \mathrm{1}$. The electron Hall current contribution is a driving term from the ionospheric electric field E since Hall conductivity σ_EH∕B is much higher than Pedersen conductivity ${\mathit{\sigma }}_{\mathrm{EP}}\sim {\mathit{\sigma }}_{\mathrm{EH}}{\mathit{\omega }}_{\mathrm{ci}}/{\mathit{\nu }}_{\mathrm{i}}$ due to the fact that for the E-layer typical conditions ${\mathit{\omega }}_{\mathrm{ci}}/{\mathit{\nu }}_{\mathrm{i}}\ll \mathrm{1}$, ions could be considered to be unmagnetized. Electrons are magnetized and frozen in the external magnetic field, experiencing only drift perpendicular to the magnetic field. That is why the parallel conductivity is high, ${\mathit{\sigma }}_{E\left|\right|}\sim {\mathit{\sigma }}_{\mathrm{EP}}{\mathit{\omega }}_{\mathrm{ce}}/{\mathit{\nu }}_{\mathrm{e}}$, because ${\mathit{\omega }}_{\mathrm{ce}}/{\mathit{\nu }}_{\mathrm{e}}\gg \mathrm{1}$, ending with the equation for the electric current as

$$\begin{array}{}\text{(A6)}& \mathit{j}=en(\mathit{v}-{\mathit{v}}_{\mathrm{e}}),\end{array}$$

known as noninductive approximation (for more details, see Sect. 7, especially 7.2 of Schunk and Nagy, 2009). Eq. (A5) is the same as Eq. (2) in the main text.

Appendix B: Finite thickness approximation

We have restricted the problem to studying the two-dimensional motion on the horizontal surface Eq. (6); therefore, we must solve the three-dimensional Poisson equation for a two-dimensional geometry. To develop an analytical theory, we need an appropriate approximation of Eq. (3).

We assume that the three-dimensional potential and density may be written in the neighborhood of z=0 in the forms of

$$\begin{array}{}\text{(B1)}& {\displaystyle }\mathrm{\Phi }(r,\mathit{\theta },z)=\mathit{\varphi }(r,\mathit{\theta })f\left(z\right),\text{(B2)}& {\displaystyle }\mathit{\rho }(r,\mathit{\theta },z)=\mathit{\sigma }(r,\mathit{\theta })g\left(z\right).\end{array}$$

Integrating the last equation with respect to z, we obtain

$$\begin{array}{}\text{(B3)}& -A{\mathrm{\nabla }}_{⟂}^{\mathrm{2}}\mathit{\varphi }+B\mathit{\varphi }=\mathit{\sigma },\end{array}$$

where ${\mathrm{\nabla }}_{⟂}^{\mathrm{2}}$ is the two-dimensional Laplacian in the horizontal surface, $A=\frac{a}{c}$, $B=\frac{b}{c}$

$$\begin{array}{}\text{(B4)}& {\displaystyle }a=\underset{-D}{\overset{D}{\int }}f\left(z\right)\mathrm{d}z,\text{(B5)}& {\displaystyle }b=\underset{-D}{\overset{D}{\int }}{f}^{\prime \prime }\left(z\right)\mathrm{d}z,\end{array}$$

and

$$\begin{array}{}\text{(B6)}& c=-\underset{-D}{\overset{D}{\int }}g\left(z\right)\mathrm{d}z.\end{array}$$

The conventional Lin–Shu approximation for an infinitely thin disk corresponds to the limit of B=0 which is obtained for g(z)=δ(z). All details about the normalization of the variables and separation of ambient and fluctuation parts are given in Vukcevic (2019). In order to obtain Eq. (15), we start from Eq. (12) in the following form:

$$\begin{array}{}\text{(B7)}& {\displaystyle \frac{\partial \mathit{\sigma }}{\partial t}}+\mathrm{\nabla }\cdot \left(\mathit{\sigma }\mathit{v}\right)=\mathrm{0},\end{array}$$

where $\mathit{v}=\mathrm{\nabla }\mathit{\varphi }\times {\mathit{e}}_z$ and $\mathit{\sigma }=-A{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+B\mathit{\varphi }$. The second term of Eq. (A1) reads as

$$\begin{array}{}\text{(B8)}& \mathrm{\nabla }\cdot \left(\mathit{\sigma }\mathit{v}\right)={\mathit{v}}_{\mathrm{0}}\mathrm{\nabla }\mathit{\sigma }+\mathit{v}\mathrm{\nabla }{\mathit{\sigma }}_{\mathrm{0}}+\mathit{v}\mathrm{\nabla }\mathit{\sigma },\end{array}$$

since $\mathrm{\nabla }\mathit{v}=\mathrm{\nabla }{\mathit{v}}_{\mathrm{0}}=\mathrm{0}$. Then, each term will be

$$\begin{array}{}\text{(B9)}& {\displaystyle }\begin{array}{rl}{\mathit{v}}_{\mathrm{0}}\mathrm{\nabla }\mathit{\sigma }& =(\mathrm{\nabla }{\mathit{\varphi }}_{\mathrm{0}}\times {\mathit{e}}_z)\cdot \mathrm{\nabla }(-A{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+B\mathit{\varphi })\\ & =A{\mathit{\varphi }}_{\mathrm{0}}^{\prime }{\displaystyle \frac{\partial }{\partial y}}{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }-B{\mathit{\varphi }}_{\mathrm{0}}^{\prime }{\displaystyle \frac{\partial \mathit{\varphi }}{\partial y}},\end{array}\text{(B10)}& {\displaystyle }\mathit{v}\mathrm{\nabla }{\mathit{\sigma }}_{\mathrm{0}}=(\mathrm{\nabla }\mathit{\varphi }\times {\mathit{e}}_z){\displaystyle \frac{\partial }{\partial x}}{\mathit{\sigma }}_{\mathrm{0}}\left(x\right)={\mathit{\sigma }}_{\mathrm{0}}^{\prime }{\displaystyle \frac{\partial \mathit{\varphi }}{\partial y}}\text{(B11)}& {\displaystyle }\begin{array}{rl}\mathit{v}& \mathrm{\nabla }\mathit{\sigma }=(\mathrm{\nabla }\mathit{\varphi }\times {\mathit{e}}_z)\cdot \mathrm{\nabla }(-A{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+B\mathit{\varphi })\\ & =-A^{\prime }{\displaystyle \frac{\partial \mathit{\varphi }}{\partial y}}{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }-A(\mathrm{\nabla }\mathit{\varphi }\times \mathrm{\nabla }){\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+B^{\prime }\mathit{\varphi }{\displaystyle \frac{\partial \mathit{\varphi }}{\partial y}}.\end{array}\end{array}$$

Collecting all these terms, neglecting the first term in the last equation as a higher-order nonlinear term, Eq. (B1) reads as

$$\begin{array}{}\text{(B12)}& \begin{array}{rl}{\displaystyle \frac{\partial }{\partial t}}& (-A{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+B\mathit{\varphi })+{\displaystyle \frac{\partial \mathit{\varphi }}{\partial y}}({\mathit{\sigma }}_{\mathrm{0}}^{\prime }-B{\mathit{\varphi }}_{\mathrm{0}}^{\prime })-A(\mathrm{\nabla }\mathit{\varphi }\times \mathrm{\nabla })\\ & {\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+{\mathit{\varphi }}_{\mathrm{0}}^{\prime }A{\displaystyle \frac{\partial }{\partial y}}{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{B}^{\prime }{\displaystyle \frac{\partial {\mathit{\varphi }}^{\mathrm{2}}}{\partial y}}=\mathrm{0}.\end{array}\end{array}$$

In order to show that the solitary vortex solution satisfies the last equation, we assume the solution to be a function $\mathit{\varphi }=\mathit{\varphi }(y-ut,x)$, so that the derivative with respect to time will become $\frac{\partial }{\partial t}=-u\frac{\partial }{\partial y}$, and consequently Eq. (B6) will read as

$$\begin{array}{}\text{(B13)}& \begin{array}{rl}-u& {\displaystyle \frac{\partial }{\partial y}}B\mathit{\varphi }+uA{\displaystyle \frac{\partial }{\partial y}}{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+{\displaystyle \frac{\partial \mathit{\varphi }}{\partial y}}({\mathit{\sigma }}_{\mathrm{0}}^{\prime }-B{\mathit{\varphi }}_{\mathrm{0}}^{\prime })-A(\mathrm{\nabla }\mathit{\varphi }\times \mathrm{\nabla })\\ & {\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+{\mathit{\varphi }}_{\mathrm{0}}^{\prime }A{\displaystyle \frac{\partial }{\partial y}}{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{B}^{\prime }{\displaystyle \frac{\partial {\mathit{\varphi }}^{\mathrm{2}}}{\partial y}}=\mathrm{0},\end{array}\end{array}$$

or

$$\begin{array}{}\text{(B14)}& \begin{array}{rl}A({\mathit{\varphi }}_{\mathrm{0}}+u)& {\displaystyle \frac{\partial }{\partial y}}{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+{\displaystyle \frac{\partial \mathit{\varphi }}{\partial y}}({\mathit{\sigma }}_{\mathrm{0}}^{\prime }-B({\mathit{\varphi }}_{\mathrm{0}}^{\prime }+u\left)\right)+A(\mathrm{\nabla }\mathit{\varphi }\times \mathrm{\nabla })\\ & {\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{B}^{\prime }{\displaystyle \frac{\partial {\mathit{\varphi }}^{\mathrm{2}}}{\partial y}}=\mathrm{0}.\end{array}\end{array}$$

Equation (B13) is the same as Eq. (15) after normalizing soliton velocity u by 2(Ω+H). If $u\gg {\mathit{\varphi }}_{\mathrm{0}}^{\prime }$ we can further simplify the equation having in the first two terms instead of $(u+{\mathit{\varphi }}_{\mathrm{0}}^{\prime })$ just u. Dividing it by uA, one gets

$$\begin{array}{}\text{(B15)}& \begin{array}{rl}{\displaystyle \frac{\partial }{\partial y}}& {\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+{\displaystyle \frac{\mathrm{1}}{u}}(\mathrm{\nabla }\mathit{\varphi }\times \mathrm{\nabla }){\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }-{\displaystyle \frac{\mathrm{1}}{A}}\left(B-{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{0}}^{\prime }}{u}}\right){\displaystyle \frac{\partial \mathit{\varphi }}{\partial y}}\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}uA}}{B}^{\prime }{\displaystyle \frac{\partial {\mathit{\varphi }}^{\mathrm{2}}}{\partial y}}=\mathrm{0}.\end{array}\end{array}$$

Next, we show that looking for the solution of that equation in the form

$$\begin{array}{}\text{(B16)}& {\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }=\mathit{\lambda }\left(x\right)\mathit{\varphi }+\mathit{\nu }\left(x\right){\mathit{\varphi }}^{\mathrm{2}}\end{array}$$

will lead to vanishing of the term related to B^′. Acting by operator $\frac{\partial }{\partial y}+\frac{\mathrm{1}}{u}[\mathrm{\nabla }\mathit{\varphi }\times \mathrm{\nabla }{]}_z$ on all parts of Eq. (B10) and neglecting terms on the order ϕ³, we get

$$\begin{array}{}\text{(B17)}& \begin{array}{rl}{\displaystyle \frac{\partial }{\partial y}}& {\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+{\displaystyle \frac{\mathrm{1}}{u}}(\mathrm{\nabla }\mathit{\varphi }\times \mathrm{\nabla }){\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }=\mathit{\lambda }\left(x\right){\displaystyle \frac{\partial \mathit{\varphi }}{\partial y}}-{\displaystyle \frac{{\mathit{\lambda }}^{\prime }}{\mathrm{2}u}}{\displaystyle \frac{\partial {\mathit{\varphi }}^{\mathrm{2}}}{\partial y}}\\ & +\mathit{\nu }{\displaystyle \frac{\partial {\mathit{\varphi }}^{\mathrm{2}}}{\partial y}}.\end{array}\end{array}$$

If Eq. (B10) satisfies Eq. (B9), coefficients of corresponding terms must be equal, which gives

$$\begin{array}{}\text{(B18)}& \mathit{\lambda }\left(x\right)={\displaystyle \frac{\mathrm{1}}{A}}\left(B-{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{0}}^{\prime }}{u}}\right)\end{array}$$

and

$$\begin{array}{}\text{(B19)}& \mathit{\nu }\left(x\right)={\displaystyle \frac{{\mathit{\lambda }}^{\prime }}{\mathrm{2}u}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}uA}}{B}^{\prime }.\end{array}$$

Since

$$\begin{array}{}\text{(B20)}& {\mathit{\lambda }}^{\prime }={\displaystyle \frac{B^{\prime }A-B{A}^{\prime }}{A^{\mathrm{2}}}}-{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{0}}^{\prime \prime }A-{\mathit{\sigma }}_{\mathrm{0}}^{\prime }{A}^{\prime }}{A^{\mathrm{2}}u}},\end{array}$$

we have

$$\begin{array}{}\text{(B21)}& \mathit{\nu }\left(x\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}u}}{\displaystyle \frac{B^{\prime }A-B{A}^{\prime }}{A^{\mathrm{2}}}}-{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{0}}^{\prime \prime }A-{\mathit{\sigma }}_{\mathrm{0}}^{\prime }{A}^{\prime }}{\mathrm{2}{A}^{\mathrm{2}}{u}^{\mathrm{2}}}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}uA}}{B}^{\prime }.\end{array}$$

The first and last terms give zero, so it becomes

$$\begin{array}{}\text{(B22)}& \mathit{\nu }\left(x\right)=-{\displaystyle \frac{uB{A}^{\prime }+({\mathit{\sigma }}_{\mathrm{0}}^{\prime \prime }A-{\mathit{\sigma }}_{\mathrm{0}}^{\prime }{A}^{\prime })}{\mathrm{2}{u}^{\mathrm{2}}{A}^{\mathrm{2}}}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}u}}\left(\mathit{\lambda }{A}^{\prime }+{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{0}}^{\prime \prime }}{u}}\right).\end{array}$$

Details for derivation of a nonlinear equation and its solution in the case when inertial velocity is not constant but rather x or y dependent can be found in Appendix B of Vukcevic (2019). In that case drift velocity has to be approximated by $\mathit{v}=\frac{\mathrm{1}}{\mathrm{\Omega }}\mathrm{\nabla }\mathit{\varphi }\times {\mathit{e}}_z$, where Ω is not constant any more, which implies ∇v≠0. Note: within Appendix B, scalar B indicates layer thickness, not magnetic field, while B^′ indicates thickness gradient.