the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Negative differential resistance, instability, and critical transition in lightning leader
Chao Xin
Liwen Xu
Ping Yuan
Yijun Zhang
Mingli Chen
The phenomena of leader extinction and restrike during lightning events, such as multiple strokes in ground flashes or recoil leaders in cloud flashes, present significant challenges. A key aspect of this issue involves the discussion of the channel's negative differential resistance and its instability. From the perspective of bifurcation theory in nonlinear dynamics, this paper suggests an inherent consistency among the channel's negative differential resistance, channel instability, and critical transition from insulation to conduction. This study examines the differential-resistance characteristics of the leader–streamer system in lightning development. We correlate the differential-resistance characteristics of the leader–streamer channel with the channel's state and instability transitions, investigating the critical current and potential difference conditions required for the stable transition of the leader–streamer channel.
- Article
(819 KB) - Full-text XML
- BibTeX
- EndNote
We affirm that all third-party copyrighted material used in this paper has been obtained with proper permissions. All such material is appropriately cited in the text and captions. Any distribution licenses different from the standard CC BY (Creative Commons Attribution) license are clearly stated below.
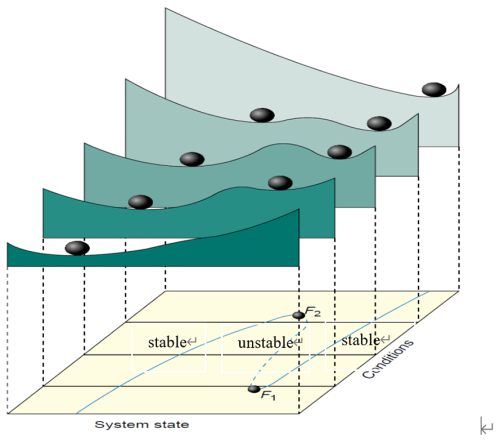
Figure 2: Adapted from “Catastrophic regime shifts in ecosystems: Linking theory to observation”, by Marten Scheffer and Stephen R. Carpenter, published in Trends in Ecology & Evolution. Used with permission from Elsevier.
Natural lightning exhibits distinct intermittent characteristics that differentiate it from long-gap discharges observed in laboratory settings (Gou et al., 2010, 2018a; Iudin et al., 2022). This intermittency is intrinsically linked to the fractal structure and critical dynamics of the lightning process (Bulatov et al., 2020; Gou et al., 2018b; Sterpka et al., 2021; Iudin and Syssoev, 2022; Syssoev et al., 2022). Additionally, the inherent polarity asymmetry in bidirectional leader development introduces instability into the discharge process, leading to destabilization and re-excitation phenomena in various lightning events (Van der Velde and Montanya, 2013; Williams, 2006; Williams and Heckman, 2012; Iudin, 2021; da Silva et al., 2023; Scholten et al., 2023).
The intermittent nature of lightning is particularly evident in ground flashes, where negative ground flash discharges are characteristically separated by extended periods of dim luminosity. These periods are marked by a distinctive sequence: when the downward negative channel decays and eventually terminates, the still-active intracloud positive component intermittently creates conditions that facilitate the formation of dart or dart-stepped leaders (Van der Velde and Montanya, 2013; Stock et al., 2014, 2023; Lapierre et al., 2017; Jensen et al., 2023). A similar intermittent behavior is observed in cloud flashes, where the active positive leader exhibits marked temporal asymmetry compared to the negative leader, resulting in K processes or recoil leaders within the cloud. These transient phenomena are generally attributed to channel instability, which manifests primarily through negative-differential-resistance characteristics of the channel (Williams and Heckman, 2012; Mazur, 2016b).
In gas discharge physics, negative differential resistance is fundamentally associated with bistability, hysteresis, and critical transitions (Bosch and Merlino, 1986; Lozneanu et al., 2002; Agop et al., 2012; Raizer and Mokrov, 2013). In lightning discharges, the leader and streamer form a strongly coupled system with complex interactions: streamers supply the energy and current essential for leader development, while the highly conductive leader channel maintains the electric field and potential required for continuous streamer propagation. Given this intricate coupling, this study expands the investigation of negative-differential-resistance properties to encompass the entire leader–streamer system rather than focusing solely on the leader channel. Our analysis specifically examines the stability characteristics during lightning development and identifies the critical conditions – in terms of current and potential difference – that govern channel stability.
2.1 Negative differential resistance in lightning
Lightning, as a natural large-scale arc discharge, exhibits negative-differential-resistance characteristics in its channel (Heckman, 1992; da Silva et al., 2019). This behavior manifests when channel temperature and conductivity increase with the current, leading to a decrease in the internal electric field needed to maintain the current, thus reducing the voltage across the channel (). This characteristic was identified by Krehbiel et al. (1979) as a potential mechanism for channel attenuation.
Heckman (1992) and Williams and Heckman (2012) investigated how negative differential resistance relates to the multiplicity of negative ground flashes. They proposed that, while a channel with negative differential resistance connected to an extended streamer source is inherently unstable, parallel channel resistance and capacitance could provide stabilization. Specifically, channel stability occurs when the electrical response time constant (RC) exceeds the thermal attenuation constant τ with a critical stability current of approximately 100 A (Heckman, 1992; Williams, 2006; Williams and Heckman, 2012).
However, Mazur and Ruhnke (2014) and Mazur (2016a, b) challenged the appropriateness of modeling the leader channel as a parallel RC circuit. They argued that channel stability depends primarily on the minimum potential difference in the streamer zone at the channel tip rather than on negative-differential-resistance characteristics (Bazelyan and Raizer, 2000; Mazur, 2016a). Given that leader development is guided by numerous streamers at the front, we suggest that differential-resistance analysis should consider both the leader channel and its associated streamers.
2.2 Negative differential resistance and bistability
To understand how negative differential resistance leads to bistability in lightning channels, we use a normalized relationship between current J and voltage φ that captures the essential nonlinear dynamics of the discharge process. This relationship emerges from the fundamental physics of plasma channel formation and maintenance (Agop et al., 2012; Manea et al., 2013):
where a is a dimensionless control parameter that governs the system's nonlinear characteristics.
As illustrated in Fig. 1 (Manea et al., 2013), for parameter a=18, the J−φ characteristic curve exhibits three distinct regions. There are two stable regions where , namely a low-conductivity state (segment AB) and a high-conductivity state (segment CD), both of which are characterized by a monotonically increasing current with voltage. These stable regions are separated by an unstable region where , demonstrating negative differential resistance. The system displays bistability, with critical transitions occurring between the two stable states: at point B, the system abruptly transitions from the low-conductivity state to the high-conductivity state, while at point D, it reverts to the low-conductivity state. This results in hysteretic behavior, where the system follows different paths during voltage increases (A → B → C) and decreases (C → D → A).
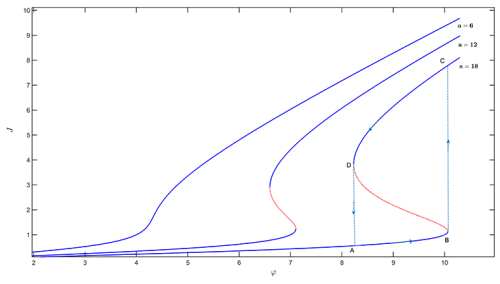
Figure 1Theoretical dependence of the normalized current on the normalized potential (adapted from Manea et al., 2013; original figure licensed under CC BY 4.0).
In nonlinear dynamics, negative differential resistance, bistability, and hysteresis are commonly observed. Considering the dynamic system, , where J is the state variable, and φ,a is a parameter. The equilibrium points are given by . At an equilibrium point, the system is unstable when and stable when .
Let us define
Then
From Eq. (1), at equilibrium, we have , and . The stability condition is equivalent to , which corresponds to negative differential resistance. This mathematical analysis provides insight into how the sign of channel differential resistance determines the stability of lightning channel states and their transitions
Similar bistability, hysteresis, and critical transitions are widely observed in biological, atmospheric, ecological, and other systems, and they can be described by similar dynamical systems (Scheffer and Carpenter, 2003; Scheffer, 2009). The generation of instability and bistability can be illustrated by the rolling-ball model shown in Fig. 2, where the peaks and valleys represent unstable and stable points, respectively. Instability triggered by strong nonlinearities (positive feedback) is an important factor causing the bistability (polymorphism) of the system and the critical transition.
2.3 The relationship between lightning channel electric field and current
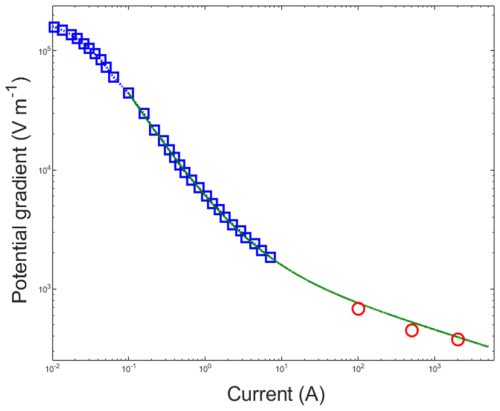
The differential-resistance characteristics of a gas discharge gap at the centimeter scale were first measured by King (1961). However, due to the effect of electrode vaporization, as pointed out by Mazur and Ruhnke (2014), King's results are only applicable to currents of less than 10 A with short gaps. In larger-scale lightning channels, the relationship between current and electric field is generally expressed in a power-law form. For example, Bazelyan et al. (2008) assumed that the leader channel current is inversely proportional to the electric field, or ; meanwhile, Larsson et al. (2005) proposed that the relationship between channel current and electric field can be described as follows:
This is consistent with the observations of Tanaka et al. (2003) and aligns with the suggestions of da Silva et al. (2019), who suggested that the power law varies for different segments within the range of 102 to 104 A.
To develop a comprehensive description of the channel's electrical characteristics across different current regimes, we combined two complementary datasets:
-
King (1962) data for I<10 A, characterizing the initial breakdown phase where electrode effects dominate;
-
Larsson et al. (2005) measurements for I>10 A, representing the fully developed leader channel.
The combined dataset was then fitted using a double power-law model that captures both regimes:
where a=4278, , c=1799, and . The minimum current used for fitting was approximately 0.1 A.
Figure 3 shows the relationship between the electric field and current, with squares representing King's observations, circles representing Tanaka et al.'s (2003) experiments, and the solid green line representing the fitted curve.
2.4 Differential resistance of the leader–streamer channel
The resistance of a streamer channel is determined by the potential difference ΔUT across the streamer zone of the leader head and the channel current I, which can be expressed as follows (Bazelyan and Raizer, 2000):
where qc represents the channel charge line density, and VL is the channel development speed. The relationship between VL and I follows a power-law form (Bazelyan and Raizer, 2000; Popov, 2009):
Since the power exponent α varies significantly in different studies, such as (Hutzler and Hutzler, 1982; Bazelyan et al., 2007) and α≈0.66 (Kekez and Savic, 1983), this study adopts and α=0.67 based on more recent works (Andreev et al., 2008; Popov, 2009; Bazelyan et al., 2009).
From Eqs. (6) and (7), we derive the voltage drop across the streamer zone at the leader head:
Considering the leader channel potential drop UC=LE – where L is the leader channel length, and E is the electric field of the channel as shown in Eq. (4) – and the streamer channel potential drop ΔUT from Eq. (8), the total potential drop U of the leader–streamer system is as follows:
Differentiating both sides with respect to I, we obtain the total differential resistance:
Figure 4 illustrates how the differential resistance varies with channel current for different leader channel lengths, where the horizontal line represents zero differential resistance. The point at which the curve intersects the horizontal line marks a change in the sign of the differential resistance, with the corresponding current at this intersection representing the critical current.
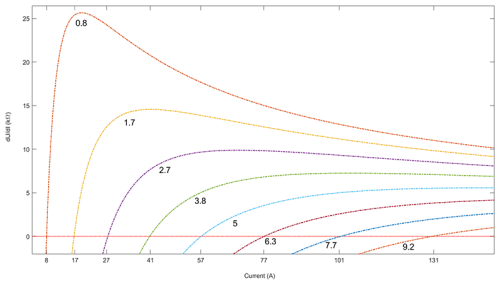
Figure 4Dependence of total differential resistance of channel on current with varying channel lengths (km). The horizontal line represents zero resistance.
Figure 5 shows that both the critical currents and the critical potential differences in the streamer zone at the leader head increase with the channel length, which is consistent with theoretical predictions. This trend aligns with Heckman's (1992) study on critical currents and supports the threshold condition for the critical potential difference proposed by Bazelyan and Raizer (2000) and Mazur (2016a).
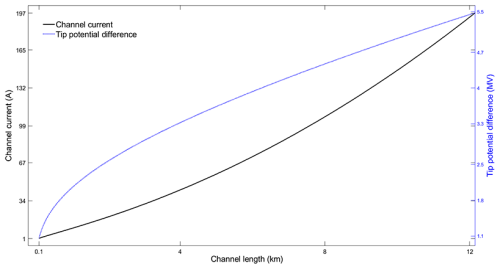
Figure 5Critical channel current and potential difference of the streamer channel at the leader tip vary with channel length.
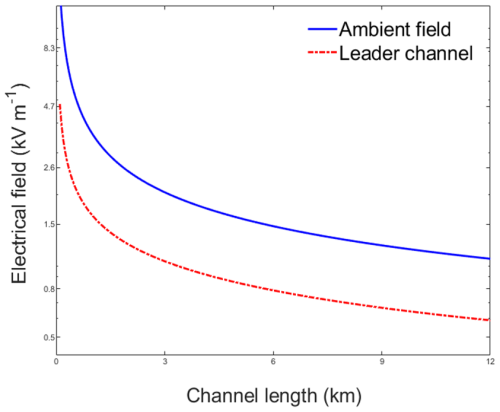
As the leader channel length increases, the ambient (stabilized) electric field decreases. Between 0.1 and 12 km, the stabilized leader–streamer field drops from 15.5 to 1.1 kV m−1. This trend is consistent with the findings of Lalande et al. (2002) and Becerra and Cooray (2006), who reported that the leader channel's ambient electric field decreases with channel height. Similarly, the internal electric field of the leader channel decreases (Fig. 6). At a length of 0.1 km, the electric field is approximately 4.9 kV m−1, while at 12 km, it drops to 0.65 kV m−1. Syssoev and Shcherbakov (2001) found that stable thermal leader channels with long electric fields (30–50 m) had electric fields of around 3–10 kV m−1, which is consistent with our results.
This paper extends the discussion on lightning discharge channel stability and differential resistance from the leader channel to the leader–streamer system. Using bifurcation theory and critical-transition theory from nonlinear dynamics, we studied the extinction, re-excitation, and critical transition of intermittent events (such as recoil leaders) in the lightning process. By analyzing the sign changes in the differential resistance of the leader–streamer system, we determined the critical current and the critical potential difference at the channel end. Our results show that, as the channel length increases, both the critical current and the critical potential difference at the channel end increase. Meanwhile, the average ambient electric field and the electric field required for stable transmission gradually decrease after an initial sharp drop. These findings are consistent with existing research.
The exact mechanism behind the sudden change in channel conductivity remains unclear, but it is likely to be related to instability caused by positive feedback within the channel. The re-excitation of a decayed leader channel is typically due to the uneven distribution of the current and electric field, which becomes more pronounced with increasing channel length. This asymmetry is particularly evident in the channel structure: the leader head maintains higher charge concentration and conductivity, remaining active and often merging with adjacent channels, while the rear part exhibits lower conductivity and greater susceptibility to disconnection and splitting
In the case of negative ground flashes, the electric field in the upper channel becomes non-uniform due to the low current in the positive leader section, which is insufficient to maintain conductivity in the lower channel. Recent observations show that the low current in the positive leader and poor conductivity in the rear section lead to negative charge deposition in the center of the rear channel. This creates negatively polarized needle structures that trigger nonlinear instability (Williams and Montanya, 2019; Hare et al., 2019, 2021; Pu and Cummer, 2019). The current in the rear positive leader decreases, leading to disconnection from the negative leader. The increased potential difference at the paused negative leader causes re-breakdown and reconnection, resulting in multiple strokes. In contrast, positive ground flashes feature a stronger current at the negative leader head, making the channel less prone to splitting, which typically results in a single stroke.
The transition from a semiconductor to a conductive state in the leader channel may be driven by ionization–thermal instability caused by positive feedback. As shown in previous studies (Bazelyan and Raizer, 2000; Popov, 2009; da Silva et al., 2019), the pulsed mechanism of the stepped leader is related to electric-field inhomogeneity among the streamers at the leader head (Syssoev and Iudin, 2023). This instability may exacerbate the electrical inhomogeneity in the streamer zone, which is thought to be triggered by attachment instability (Douglas-Hamilton and Mani, 1974; Sigmond, 1984; Luque et al., 2016; Malagón-Romero and Luque, 2019; Malagón-Romero, 2021). If the mechanism in positively stepped leaders is similar to that of negatively stepped leaders, the excitation of the leader should occur in the streamer zone at the leader head (Tran and Rakov, 2016; Kostinskiy et al., 2018; Huang et al., 2020; Wang et al., 2020).
Furthermore, the inhomogeneities, instabilities, and critical transitions observed in the leader channel and streamer zone, whether during initiation or transmission, as well as the emergence of pulse events of various scales and the interactions between leader channels, streamers, and other streamers, all exhibit collective, fractal, and critical properties. These phenomena may require more unified explanations based on fractal analysis and critical dynamics.
The dataset used in this study is openly available at https://doi.org/10.5281/zenodo.14917985 (Gou et al., 2025).
XG: conceptualization, methodology, software, validation, formal analysis, investigation, writing (original draft; review and editing), visualization, supervision, project administration. LX, CX: software, formal analysis. PY, YZ, MC: writing (review and editing).
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The work leading to this paper was supported, in part, by the National Natural Science Foundation of China (grant nos. 42065005, 42175100, and 42175090) and, in part, by the Hong Kong Polytechnic University through the Research Grants Council of Hong Kong under grant no. GRF15215120.
This research has been supported by the National Natural Science Foundation of China (grant nos. 42065005, 42175100, and 42175090) and the Hong Kong Polytechnic University (grant no. GRF15215120).
This paper was edited by Ana M. Mancho and Vincenzo Carbone and reviewed by three anonymous referees.
Agop, M., Nica, P., Niculescu, O., and Dimitriu, D.-G.: Experimental and Theoretical Investigations of the Negative Differential Resistance in a Discharge, Plasma, 81, 064502, https://doi.org/10.1143/JPSJ.81.064502, 2012.
Andreev, A. G., Bazelyan, E. M., Bulatov, M. U., Kuzhekin, I. P., Makalsky, L. M., Sukharevskij, D. I., and Syssoev, V. S.: Experimental study of the positive leader velocity as a function of the current in the initial and final-jump phases of a spark discharge, Plasma Phys. Rep., 34, 609–615, https://doi.org/10.1134/S1063780X0807009X, 2008.
Bazelyan, E., Sysoev, V., and Andreev, M.: Numerical simulations of spark channels propagating along the ground surface: Comparison with high-current experiment, Plasma Phys. Rep., 35, 702–707, https://doi.org/10.1134/S1063780X0908011X, 2009.
Bazelyan, E. M. and Raizer, Y. P.: Lightning Physics and Lightning Protection. IOP Publishing, Bristol, 27–221, https://doi.org/10.1201/9780367801533, 2000.
Bazelyan, E. M., Aleksandrov, N. L., Raizer, Y. P., and Konchakov, A. M.: The effect of air density on atmospheric electric fields required for lightning initiation from a long airborne object, Atmos. Res., 86, 126–138, https://doi.org/10.1016/j.atmosres.2007.03.007, 2007.
Bazelyan, E. M., Raizer, Y. P., and Aleksandrov, N. L.: Corona initiated from grounded objects under thunderstorm conditions and its influence on lightning attachment, Plasma Sour. Sci. Technol., 17, 024015, https://doi.org/10.1088/0963-0252/17/2/024015, 2008.
Becerra, M. and Cooray, V.: A simplified physical model to determine the lightning upward connecting leader inception, IEEE T. Power Deliv., 21, 897–908, https://doi.org/10.1109/TPWRD.2005.858774, 2006.
Bosch, R. A. and Merlino, R. L.: Sudden Jumps, Hysteresis, and Negative Resistance in an Argon Plasma Discharge. I. Discharges with No Magnetic Field, Beitr. Plasmaphys., 26, 1–12, https://doi.org/10.1002/ctpp.19860260102, 1986.
Bulatov, A. A., Iudin, D. I., and Sysoev, A. A.: Self-Organizing Transport Model of a Spark Discharge in a Thunderstorm Cloud, Radiophys. Quant. El., 63, 124–141, https://doi.org/10.1007/s11141-020-10041-z, 2020.
da Silva, C. L., Sonnenfeld, R. G., Edens, H. E., Krehbiel, P. R., Quick, M. G., and Koshak, W. J.: The plasma nature of lightning channels and the resulting nonlinear resistance, J. Geophys. Res.-Atmos., 124, 9442–9463, https://doi.org/10.1029/2019JD030693, 2019.
da Silva, C. L., Winn, W. P., Taylor, M. C., Aulich, G. D., Hunyady, S. J., Eack, K. B., Edens, H. E., Sonnenfeld, R. G., Krehbiel, P. R., Eastvedt, E. M., and Trueblood, J. J.: Polarity asymmetries in rocket-triggered lightning, Geophys. Res. Lett., 50, e2023GL105041, https://doi.org/10.1029/2023GL105041, 2023.
Douglas-Hamilton, D. H. and Mani, S. A.: Attachment instability in an externally ionized discharge, J. Appl. Phys., 45, 4406, https://doi.org/10.1063/1.1663065, 1974.
Gou, X., Chen, M., Du, Y., and Dong, W.: Fractal dynamics analysis of the VHF radiation pulses during initial breakdown process of lightning, Geophys. Res. Lett., 37, L11808, https://doi.org/10.1029/2010GL043178, 2010.
Gou, X., Chen, M., and Zhang, G.: Time correlations of lightning flash sequences in thunderstorms revealed by fractal analysis, J. Geophys. Res.-Atmos., 123, 1351–1362, https://doi.org/10.1002/2017JD027206, 2018a.
Gou, X. Q., Zhang, Y. J., Li, Y. J., and Chen, M. L.: Theory and observation of bidirectional leader of lightning: Polarity asymmetry, instability, and intermittency, Acta Phys. Sin., 67, 205201, https://doi.org/10.7498/aps.67.20181079, 2018b.
Gou, X., Xin, C., Xu, L., Yuan, P., Zhang, Y., and Chen, M.: Negative Differential Resistance, Instability, and Critical Transition in Lightning Leader (MATLAB Code, Data, and Figures), Zenodo [data set], https://doi.org/10.5281/zenodo.14917985, 2025.
Hare, B. M., Scholten, O., Dwyer, J., Trinh, T. N. G., Buitink, S., ter Veen, S., Bonardi, A., Corstanje, A., Falcke, H., Hörandel, J. R., Huege, T., Mitra, P., Mulrey, K., Nelles, A., Rachen, J. P., Rossetto, L., Schellart, 1 P., Winchen, T., Anderson, J., Avruch, I. M., Bentum, M. J., Blaauw, R., Broderick, J. W., Brouw, W. N., Brüggen, M., Butcher, H. R., Ciardi, B., Fallows, R. A., de eus, E., Duscha, S., Eislöffel, J., Garrett, M. A., Grießmeier, J. M., Gunst, A. W., van Haarlem, M. P., Hessels, J. W. T., Hoeft, M., van der Horst, A. J., Iacobelli, M., Koopmans, L. V. E., Krankowski, A., Maat, P., Norden, M. J., Paas, H., Pandey-Pommier, M., Pandey, V. N., Pekal, R., Pizzo, R., Reich, W., Rothkaehl, H., Röttgering, H. J. A., Rowlinson, A., Schwarz, D. J., Shulevski, A., Sluman, J., Smirnov, O., Soida, M., Tagger, M., Toribio, M. C., van Ardenne, A., Wijers, R. A. M. J., van Weeren, R. J., Wucknitz, O., Zarka, P., and Zucca, P.: Needle-like structures discovered on positively charged lightning branches, Nature, 568, 360–363, https://doi.org/10.1038/s41586-019-1086-6, 2019.
Hare, B. M., Scholten, O., Dwyer, J., Strepka, C., Buitink, S., Corstanje, A., Falcke, H., Hörandel, J. R., Huege, T., Krampah, G. K., Mitra, P., Mulrey, K., Nelles, A., Pandya, H., Rachen, J. P., Thoudam, S., Trinh, T. N. G., ter Veen, S., and Winchen, T.: Needle propagation and twinkling characteristics, J. Geophys. Res.-Atmos., 126, e2020JD034252, https://doi.org/10.1029/2020JD034252, 2021.
Heckman, S.: Why does a lightning flash have multiple strokes?, PhD thesis, Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, https://dspace.mit.edu/bitstream/handle/1721.1/17300/26622951-MIT.pdf?sequence=2 (last access: 25 April 2025), 1992.
Huang, S., Chen, W., Pei, Z., Fu, Z., Wang, L., He, T., Li, Z., Gu, J., Bian, K., Xiang, N., and Wang, Y.: The discharge preceding the intense reillumination in positive leader steps under the slow varying ambient electric field, Geophys. Res. Lett., 47, e2019GL086183, https://doi.org/10.1029/2019GL086183, 2020.
Hutzler, B. and Hutzler, D.: A model of breakdown in large air gaps, Bulletin de la DER d'EDF, serie B, 4, 11–39, 1982.
Iudin, D.: Lightning as an Asymmetric Branching Network, Atmos. Res., 256, 105560, https://doi.org/10.1016/j.atmosres.2021.105560, 2021.
Iudin, D. I. and Syssoev, A. A.: Hot Plasma Channel Network Formation in Thunderclouds, J. Atmos. Solar-Terr. Phy., 240, 105944, https://doi.org/10.1016/j.jastp.2022.105944, 2022.
Iudin, D. I., Sysoev, A. A., and Rakov, V.: Problems of Lightning Initiation and Development, Radiophys. Quant. El., 64, 780–803, https://doi.org/10.1007/s11141-022-10178-z, 2022.
Jensen, D., Shao, X. M., and Sonnenfeld, R.: Insights into Lightning K-Leader Initiation and Development from Three Dimensional Broadband Interferometric Observations, ESS Open Archive, https://doi.org/10.22541/essoar.168275995.55801872/v2, 2023.
Kekez, M. and Savic, P.: Correlation leader velocity for current varying from 90 mA to 2 kA, in: 4-th Inter. Symp. On High Voltage Engineering, 5–9 September 1993, Athens, N 45.04, 1983.
King, L. A., The voltage gradient of the free burning arc in air or nitrogen, Ionization Phenomena in Gases, in: Volume I; Proceedings of the Fifth International Conference held 28 August–1 September 1961, Hedited by: Maecker, H., North-Holland Publishing o., Amsterdam, p. 871, https://ui.adsabs.harvard.edu/abs/1962ipg1.conf..871K/abstract (last access: 25 April 2025), 1962.
Kostinskiy, A. Y., Syssoev, V. S., Bogatov, N. A., Mareev, E. A., Andreev, M. G., Bulatov, M. U., Sukharevsky, D. I., and Rakov, V. A.: Abrupt elongation (stepping) of negative and positive leaders culminating in an intense corona streamer burst: Observations in long sparks and implications for lightning, J. Geophys. Res.-Atmos., 123, 5360–5375, https://doi.org/10.1029/2017JD027997, 2018.
Krehbiel, P. R., Brook, M., and McCrory, R. A.: An analysis of the charge structure of lightning discharges to ground, J. Geophys. Res., 84, 2432–2456, https://doi.org/10.1029/JC084iC05p02432, 1979.
Lapierre, J. L., Sonnenfeld, R. G., Stock, M., Krehbiel, P. R., Edens, H. E., and Jensen, D.: Expanding on the relationship between continuing current and in-cloud leader growth, J. Geophys. Res.-Atmos., 122, 4150–4164, https://doi.org/10.1002/2016JD026189, 2017.
Lalande, P., Bondiou-Clergerie, A., Bacchiega, G., and Gallimberti, I.: Observations and modeling of lightning leaders, Comptes Rendus Physique, 3, 1375–1392, https://doi.org/10.1016/S1631-0705(02)01413-5, 2002.
Larsson, A., Delannoy, A., and Lalande, P.: Voltage drop along a lightning channel during strikes to aircraft, Atmos. Res., 76, 377–385, https://doi.org/10.1016/j.atmosres.2004.11.032, 2005.
Lozneanu, E., Popescu, V., and Sanduloviciu, M.: Negative differential resistance related to self-organization phenomena in a dc gas discharge, J. Appl. Phys., 92, 1195–1199, https://doi.org/10.1063/1.1487456, 2002.
Luque, A., Stenbaek-Nielsen, H. C., McHarg, M. G., and Haaland, R. K.: Sprite beads and glows arising from the attachment instability in streamer channels, J. Geophys. Res.-Space, 121, 2431–2449, https://doi.org/10.1002/2015JA022234, 2016.
Malagón-Romero, A. F.: Numerical investigation on the advance of leader channels in lightning and long sparks, Universidad de Granada, http://hdl.handle.net/10481/67863 (last access: 25 April 2025), 2021.
Malagón-Romero, A. and Luque, A.: Spontaneous emergence of space stems ahead of negative leaders in lightning and long sparks, Geophys. Res. Lett., 46, 4029–4038, https://doi.org/10.1029/2019GL082063, 2019.
Manea, L., Nejneru, C., Mătăsaru, D., Axinte, C., and Agop, M.: Dynamics Behaviors of a Laser Produced Plasma: Theoretical Approach, J. Mod. Phys., 4, 1013–1021, https://doi.org/10.4236/jmp.2013.47136, 2013.
Mazur, V.: Principles of Lightning Physics, IOP Publishing, Bristol, 1–183, https://doi.org/10.1088/978-0-7503-1152-6, 2016a.
Mazur, V.: The physical concept of recoil leader formation, J. Electrostat., 82, 79–87, https://doi.org/10.1016/j.elstat.2016.05.003, 2016b.
Mazur, V. and Ruhnke, L. H.: The physical processes of current cutoff in lightning leaders, J. Geophys. Res.-Atmos., 119, 2796–2810, https://doi.org/10.1002/2013JD020494, 2014.
Popov, N. A.: Study of the formation and propagation of a leader channel in air, Plasma Phys. Rep., 35, 785–793, https://doi.org/10.1134/S1063780X09090074, 2009.
Pu, Y. and Cummer, S. A.: Needles and lightning leader dynamics imaged with 100–200 MHz broadband VHF interferometry, Geophys. Res. Lett., 46, 13556–13563, https://doi.org/10.1029/2019GL085635, 2019.
Raizer, Y. P. and Mokrov, M. S.: Physical mechanisms of self-organization and formation of current patterns in gas discharges of the Townsend and glow types, Phys. Plasmas, 20, 101604, https://doi.org/10.1063/1.4823460, 2013.
Scheffer, M.: Critical Transitions in Nature and Society, in: Vol. 16, Princeton University Press, https://doi.org/10.2307/j.ctv173f1g1, 2009.
Scheffer, M. and Carpenter, S. R.: Catastrophic regime shifts in ecosystems: linking theory to observation, Trends Ecol. Evol., 18, 648–656, https://doi.org/10.1016/j.tree.2003.09.002, 2003.
Scholten, O., Hare, B., Dwyer, J., Liu, N., Sterpka, C., Mulrey, K., and TerVeen, S.: Searching for intra-cloud positive leaders in VHF, Research Square, https://doi.org/10.21203/rs.3.rs-2631381/v1, 2023.
Sigmond, R. S.: The residual streamer channel: Return strokes and secondary streamers, J. Appl. Phys., 56, 1355–1370, https://doi.org/10.1063/1.334126, 1984.
Sterpka, C., Dwyer, J., Liu, N., Hare, B. M., Scholten, O., Buitink, S., and Nelles, A.: The Spontaneous Nature of Lightning Initiation Revealed, Geophys. Res. Lett., 48, e2021GL095511, https://doi.org/10.1029/2021GL095511, 2021.
Stock, M., Tilles, J., Taylor, G. B., Dowell, J., and Liu, N.: Lightning Interferometry with the Long Wavelength Array, Remote Sens., 15, 3657, https://doi.org/10.3390/rs15143657, 2023.
Stock, M. G., Akita, M., Krehbiel, P. R., Rison, W., Edens, H. E., Kawasaki, Z., and Stanley, M. A.: Continuous broadband digital interferometry of lightning using a generalized across-correlation algorithm, J. Geophys. Res.-Atmos., 119, 3134–3165, https://doi.org/10.1002/2013JD020217, 2014.
Syssoev, A. A. and Iudin, D. I.: Numerical Simulation of Electric Field Distribution inside Streamer Zones of Positive and Negative Lightning Leaders, Atmos. Res., 295, 107021, https://doi.org/10.1016/j.atmosres.2023.107021, 2023.
Syssoev, A. A., Iudin, D. I., Iudin, F. D., Klimashov, V. Y., and Emelyanov, A. A.: Relay charge transport in thunderclouds and its role in lightning initiation, Sci. Rep., 12, 1–21, https://doi.org/10.1038/s41598-022-10722-x, 2022.
Syssoev, V. S. and Shcherbakov, Y. V.: Electrical Strength of Ultra-Long Air Gaps, SAE Technical Paper 2001-01-2898, SAE Mobilus, https://doi.org/10.4271/2001-01-2898, 2001.
Tanaka, S.-I., Sunabe, K.-Y., and Goda, Y.: Internal voltage gradient and behavior of column on long-gap DC free arc, Elect. Eng. Jpn., 144, 8–16, https://doi.org/10.1002/eej.10300, 2003.
Tran, M. D. and Rakov, V. A.: Initiation and propagation of cloud-to-ground lightning observed with a high-speed video camera, Sci. Rep., 6, 39521, https://doi.org/10.1038/srep39521, 2016.
Van der Velde, O. A. and Montanya, J.: Asymmetries in bidirectional leader development of lightning flashes, J. Geophys. Res.-Atmos., 118, 13504–13519, https://doi.org/10.1002/2013JD020257, 2013.
Wang, X., Wang, D., He, J., and Takagi, N.: A comparative study on the discontinuous luminosities of two upward lightning leaders with opposite polarities, J. Geophys. Res.-Atmos., 125, e2020JD032533, https://doi.org/10.1029/2020JD032533, 2020.
Williams, E. and Heckman, S.: Polarity asymmetry in lightning leaders: The evolution of ideas on lightning behavior from strikes to aircraft, Aerospace Lab. J., 5, 1–8, 2012.
Williams, E. and Montanya, J.: A closer look at lightning reveals needle-like structures, Nature, 568, 319–320, https://doi.org/10.1038/d41586-019-01178-7, 2019.
Williams, E. R.: Problems in Lightning Physics – the Role of Polarity Asymmetry, Plasma Sour. Sci. Technol., 15, S91–S108, https://doi.org/10.1088/0963-0252/15/2/S12, 2006.
We investigate the stability characteristics of lightning discharge channels through their differential resistance properties. Our analysis reveals that lightning channels exhibit bistable behavior, transitioning between low- and high-conductivity states depending on channel length and electric-field conditions. This work provides new insights into lightning channel dynamics and could contribute to improved lightning protection strategies.
We investigate the stability characteristics of lightning discharge channels through their...