Bridging classical data assimilation and optimal transport: the 3D-Var case

Because optimal transport (OT) acts as displacement interpolation in physical space rather than as interpolation in value space, it can avoid double-penalty errors generated by mislocations of geophysical fields. As such, it provides a very attractive metric for non-negative, sharp field comparison – the Wasserstein distance – which could further be used in data assimilation (DA) for the geosciences. However, the algorithmic and numerical implementations of such a distance are not straightforward. Moreover, its theoretical formulation within typical DA problems faces conceptual challenges, resulting in scarce contributions on the topic in the literature.

We formulate the problem in a way that offers a unified view with respect to both classical DA and OT. The resulting OTDA framework accounts for both the classical source of prior errors, background and observation, and a Wasserstein barycentre in between states which are pre-images of the background state and observation vector. We show that the hybrid OTDA analysis can be decomposed as a simpler OTDA problem involving a single Wasserstein distance, followed by a Wasserstein barycentre problem that ignores the prior errors and can be seen as a McCann interpolant. We also propose a less enlightening but straightforward solution to the full OTDA problem, which includes the derivation of its analysis error covariance matrix. Thanks to these theoretical developments, we are able to extend the classical 3D-Var/BLUE (best linear unbiased estimator) paradigm at the core of most classical DA schemes. The resulting formalism is very flexible and can account for sparse, noisy observations and non-Gaussian error statistics. It is illustrated by simple one- and two-dimensional examples that show the richness of the new types of analysis offered by this unification.

1 Introduction

1.1 Data assimilation and the double-penalty issue

Geophysical data assimilation (DA) is a set of methods and algorithms at the intersection of Earth sciences, mathematics, and computer science that are designed to enhance our understanding and predictive capability with respect to the complex systems that govern our planet (Carrassi et al., 2018). For example, these systems encompass the atmosphere, ocean, atmospheric chemistry and biogeochemistry, land surfaces, glaciology, hydrology, and climate system as a whole. DA is meant to optimally combine all sources of quantitative information, typically past and present observations, and numerical and statistical models of the system under consideration. DA is critical in forecasting chaotic geofluids by resetting the initial conditions of the flow, estimating physical and statistical parameters of the models, and providing a quantitative reanalysis of the past history of the climate system over decades. Because classical DA is applied to complex and high-dimensional dynamics, the DA algorithms often result from a compromise between the sophistication of the employed mathematical techniques and their numerical scalability and efficiency (Kalnay, 2003; Asch et al., 2016; Evensen et al., 2022). For instance, it is well-known that most DA methods are built around or from an update step – the analysis – where observations and background states are combined, an operation which often relies on Gaussian statistical assumptions.

Here, we would like to focus on one important issue that impacts classical DA, known as the double-penalty error in the geosciences. The double-penalty issue refers to the over-penalisation of errors in both the model and observational data (e.g. Amodei and Stein, 2009) and compromises the balance required for effective DA. It often stems from the mislocation of fields, which is caused by model error in either the forecasting or observation operator. A typical example is given by the slight mislocation of a plume of pollutant resulting in high predicted concentration values at positions where no pollutant is observed, while the model misses the observed concentration peaks (Farchi et al., 2016). This mismatch is heavily penalised due to the use, over the same discretised space, of the root-mean-square error (RMSE) for a point-by-point comparison. Figure 1 shows an exemplar of double-penalty error resulting in the inability to properly evaluate a model and learn from an analysis increment. This double-penalty error, a very common contribution to the representation error (Janjić et al., 2018), is ubiquitous in the geosciences, for example, in numerical weather prediction (in particular for water vapour), in atmospheric chemistry and air quality, in biogeochemistry, and in eddy-resolving ocean forecasting. This especially applies to sharp fields, whereas it may be of less relevance for smoother, larger-scale fields such as temperature.

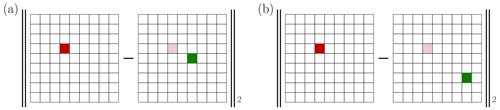
Figure 1 These two panels schematise the computation of the RMSE of two analysis increments. These increments are the difference between the truth (left mesh in between both pairs of the norm delimiters), concentrated here in the red grid cell, and the analysis, located in the green grid cells (right mesh in between both pairs of the norm delimiters). The increment in panel (a) is the outcome of a better analysis that is spatially closer to the truth, compared with that in panel (b); however, both increments yield the same RMSE. Hence, this verification metric is impacted by the double-penalty error and does not help discriminate location errors.

It has been recognised that, although it can handle amplitude and smoothness mismatch, the weighted Euclidean (Mahalanobis) distance cannot cope with mislocation error; thus, it cannot account for the full distortion between mismatched fields (Hoffman et al., 1995). In the field of precipitation verification, one would alternatively speak of amplitude, structure, and location errors (e.g. Wernli et al., 2008). Hence, even though tuning covariances of Gaussian error distributions as in classical DA, such as increasing the correlation length, might help mitigate the double-penalty error, it is insufficient. In Fig. 1, one might replace the Euclidean norm with a weighted Euclidean one with a large correlation length. This would yield similar norm values for both cases. Unfortunately, it is not difficult to show that, in this limit, this (almost singular) norm can only distinguish between the spatial mean of both fields: it became blunt with no discriminating power. With respect to DA, Feyeux et al. (2018, their Fig. 1) also illustrate why the Euclidean distance cannot properly cope with mislocation error. Note that, if Feyeux et al. (2018) had used a weighted Euclidean distance instead, with the same covariance matrix for the two contributions of the cost function, the resulting analysis state would have been the same and, in particular, independent of the covariance matrix. A similar but two-dimensional illustration is given by Vanderbecken et al. (2023, their Fig. 3).

1.2 Nonlocal verification metrics

The issue can be attributed to the use of a local verification metric, meaning that it compares, through the RMSE, values at the same site, of the same grid cell. Thus, this issue goes beyond DA and pertains to the use of local metrics.

To avoid being impacted by the double-penalty issue stemming from the use of local verification metrics, smarter nonlocal or multiscale metrics have been proposed. A typical metric of this kind consists of the combination of a displacement map followed by the use of classical norm such as the RMSE (Hoffman et al., 1995; Keil and Craig, 2009). In this vein, effective verification metrics can be based on optical flow-based warping or on deformed meshes, prior to using classical norms (Gilleland et al., 2010a, b). These metrics can also be designed as scale-dependent and possibly multiscale, based on an empirical separation of scales, such as with fuzzy metrics (Ebert, 2008; Amodei and Stein, 2009) or wavelets (Briggs and Levine, 1997). They can be designed to grasp and quantify objects and features, such as lows and highs (Davis et al., 2006a, b; Lack et al., 2010). Metrics with similar capabilities (but not necessarily based on a displacement concept) have been introduced in computer vision, such as the structural similarity index (Zhou et al., 2004), or in the verification of precipitation (Wernli et al., 2008; Skok, 2023; Necker et al., 2023).

One of the most elegant approaches is based on the theory of optimal transport (OT) and the associated Wasserstein distance, which sits on solid mathematical foundations and significant developments; these are the main reasons why we will focus on OT in the following. Examples of the application of OT to the verification of tracer and greenhouse gases models are given in Farchi et al. (2016) and Vanderbecken et al. (2023).

1.3 Optimal transport and the Wasserstein distance

Before mentioning applications of the Wasserstein distance in the field of geoscience, let us first give a very brief introduction to the concept and mathematical formulation of OT.

Figure 2 Illustration of the earth mover problem introduced by Monge in 1781 (see bulk of paper).

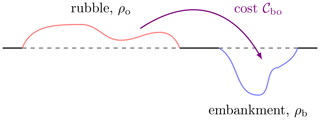
The OT concept stems from an engineering, although rather universal, problem. Gaspard Monge (Monge, 1781) considered the earth mover problem, the goal of which is to efficiently move rubble to an embankment of about the same volume (see Fig. 2). Each displacement of a bit of earth has a known cost, so that the goal is to find the cheapest deterministic map that completely moves the rubble to the embankment. In mathematical terms, the goal is to find the map of minimal cost that transports the origin measure ρ_o to the target measure ρ_b; measure here means that both of them are non-negative and are integrable of integral 1. Note that the value 1 is arbitrary here and can be changed to m>0, provided that this is the mass of both ρ_o and ρ_b. The cost is defined by a non-negative function 𝒞_bo of two variables (one for the origin space and the other for the target space). Let us assume a quadratic cost, defined for any couple of points (x,y) of a geometric domain Ω:

$$\begin{array}{}\text{(1)}& {\mathcal{C}}_{\mathrm{bo}}(x,y)={∥x-y∥}_{\mathrm{2}}^{\mathrm{2}},\end{array}$$

where ∥⋅∥₂ is the Euclidean norm. Let us define the set of all admissible differentiable maps T that transport ρ_o to ρ_b:

$$\begin{array}{}\text{(2)}& {\mathcal{U}}_{\mathrm{bo}}=\left\{T:\mathrm{\Omega }\mapsto \mathrm{\Omega },{\mathit{\rho }}_{\mathrm{o}}=\left|{\partial }_{x}T\right|{\mathit{\rho }}_{\mathrm{b}}\circ T\right\},\end{array}$$

where |∂_xT| is the absolute value of the determinant of the Jacobian of T, a factor which accounts for the deformation of the measure by the globally mass-conserving T. The square of the Wasserstein distance ${\mathcal{W}}_{{\mathcal{C}}_{\mathrm{bo}}}$ is then defined by the following:

$$\begin{array}{}\text{(3)}& {\mathcal{W}}_{{\mathcal{C}}_{\mathrm{bo}}}^{\mathrm{2}}\left({\mathit{\rho }}_{\mathrm{o}},{\mathit{\rho }}_{\mathrm{b}}\right)=\underset{T\in {\mathcal{U}}_{\mathrm{bo}}}{min}\underset{\mathrm{\Omega }}{\int }{\mathcal{C}}_{\mathrm{bo}}\left(x,T\left(x\right)\right){\mathit{\rho }}_{\mathrm{o}}\left(x\right)\mathrm{d}x.\end{array}$$

Here, the purpose is to minimise the total transport cost between ρ_o and ρ_b, and the optimal map T is often referred to as the Monge map. It can be shown that ${\mathcal{W}}_{{\mathcal{C}}_{\mathrm{bo}}}$ is indeed a proper mathematical distance. The mathematical formulation is deceptively simple, as it is elegant, concise, and easy to grasp, but its theoretical and numerical solutions are far from trivial.

In the 20th century, a breakthrough was made by Leonid Kantorovich, who promoted the Monge problem to a probabilistic formulation. From his point of view, a bit of earth can be split and moved to many sites of the target measure support. Thus, the deterministic map T is replaced with a probabilistic measure π defined over Ω×Ω. Hereafter, such a π is called a transference plan. An admissible transference plan is integrable and has ρ_o and ρ_b as one-variable marginals; hence, the definition of the admissible set is as follows:

$$\begin{array}{}\text{(4)}& {\displaystyle }\begin{array}{rl}{\mathcal{V}}_{\mathrm{bo}}=& \left\{\mathit{\pi }:\mathrm{\Omega }\times \mathrm{\Omega }\mapsto {\mathbb{R}}_{+},{\mathit{\rho }}_{\mathrm{o}}\left(x\right)=\underset{\mathrm{\Omega }}{\int }\mathit{\pi }(x,y)\mathrm{d}y,\right.\\ & \left.{\mathit{\rho }}_{\mathrm{b}}\left(y\right)=\underset{\mathrm{\Omega }}{\int }\mathit{\pi }(x,y)\mathrm{d}x\right\}.\end{array}\end{array}$$

As opposed to the deterministic Monge maps, the transference plans offer a symmetrical view of the origin and target space and their measures. An illustration of a discrete transference plan is given in Fig. 3. From this view, the squared Wasserstein distance can be reformulated as follows:

$$\begin{array}{}\text{(5)}& {\mathcal{W}}_{{\mathcal{C}}_{\mathrm{bo}}}^{\mathrm{2}}\left({\mathit{\rho }}_{\mathrm{o}},{\mathit{\rho }}_{\mathrm{b}}\right)=\underset{\mathit{\pi }\in {\mathcal{V}}_{\mathrm{bo}}}{min}\underset{\mathrm{\Omega }\times \mathrm{\Omega }}{\int }{\mathcal{C}}_{\mathrm{bo}}(x,y)\mathit{\pi }(x,y)\mathrm{d}x\mathrm{d}y.\end{array}$$

Equations (3) and (5) are the main continuous formulations of OT. In the rest of the paper, we will deal instead with discrete related formulations, which are more tangible and amenable to algorithmic and numerical implementations.

The field has attracted a lot of attention from pure and applied mathematicians as well as computer scientists. A complete introduction to the topic by experts can be found in the stimulating text books by Vilani (2003, 2009) and Peyré and Cuturi (2019). Peyré and Cuturi (2019) provide concrete examples, numerical methods, and a broad coverage of the topic from the perspective of applied mathematicians and computer scientists; hence, their work will be referred to quite often in the rest of the paper.

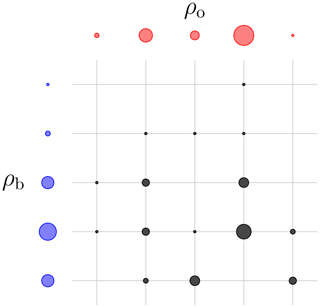
Figure 3 A representation of a discrete transport plan between two discrete origin (blue) and target (red) measures. The black dots represent the value of the transference plan. The radius of the dots is proportional to the values of these measures. This transference plan is checked to be admissible but is not necessarily optimal.

1.4 Nonlocal, multiscale metrics and data assimilation

Let us now go back to DA and narrow our focus to the use of advanced metrics in DA. Accounting for displacement error in DA, and hence relying on nonlocal verification metrics, has been advocated by Hoffman and Grassotti (1996), Ravela et al. (2007), and Plu (2013). Metrics built on a multiscale analysis of the fields to achieve a similar goal have been proposed by Ying (2019) and Ying et al. (2023).

The Wasserstein distance and closely related formulations have been advocated in the flow formulation of the analysis (DA update) to seamlessly transport the prior to the posterior (El Moselhy and Marzouk, 2012; Oliver, 2014; Marzouk et al., 2017; Farchi and Bocquet, 2018; Tamang et al., 2020). It can, for instance, be used to adjust the posterior discrete probability density functions (pdfs) in the particle filter. It has similarly been used to assist ensemble DA (Tamang et al., 2021, 2022). Finally, it has also, very recently, been used to compare forecast ensembles for sub-seasonal prediction (Le Coz et al., 2023; Lledó et al., 2023) or precipitation (Duc and Sawada, 2024).

In the context of this paper, it is critical to be aware that the use of OT in practical DA has, thus far, focused on applying OT independently to the pdf of each single scalar variable. Quite often, OT is applied to the pdf of a single random variable for the following two reasons:

• OT in one dimension (the space of the values taken by this random variable), with a quadratic cost, has a very simple solution that only relies on the cumulative distribution functions of the origin and target measures (see e.g. Remark 2.30 in Peyré and Cuturi, 2019), a technique known in statistics as quantile matching.

• Increasing the number of random variables is subject to the curse of dimensionality, necessitating an exponential increase in computational resources when increasing the resolution of the discretised fields.

This is very different from our context and objective where the objects dealt with by OT are (non-negative) physical field states, not the pdf of one of their scalar variables.

1.5 Feyeux et al. (2016) proposal

The present paper stands more in the wake of the seminal proposals of Ning et al. (2014), Feyeux (2016), and Feyeux et al. (2018). Their idea is to replace the local metrics of classical variational DA, typically the square of the Euclidean distance (hence related to the L₂ norm), with the squared Wasserstein distance. This is intuitively what we are after in order to cope with mislocation errors mentioned in Sect. 1.1 in the context of DA. This should redefine the nature of the DA update step. Let us formalise this idea (Feyeux, 2016).

We will seize this opportunity to introduce some of our notation in the context of discrete DA, which is a widely adopted standpoint in the geosciences. Let us focus on a classical DA 3D-Var cost function (Daley, 1991):

$$\begin{array}{}\text{(6)}& G_{\mathrm{cl}}\left({\mathit{x}}^{\mathrm{a}}\right)={∥{\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{a}}∥}_{\mathrm{2}}^{\mathrm{2}}+{∥{\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{a}}∥}_{\mathrm{2}}^{\mathrm{2}},\end{array}$$

where ∥⋅∥₂ is the Euclidean norm, ${\mathit{y}}^{\mathrm{b}}\in {\mathbb{R}}^{N_{\mathrm{b}}}$ is the first guess, ${\mathit{y}}^{\mathrm{o}}\in {\mathbb{R}}^{N_{\mathrm{o}}}$ is the vector of observations, and H is the observation operator.¹ ${\mathit{x}}^{\mathrm{a}}\in {\mathbb{R}}^{N_{\mathrm{a}}}$ is the dummy variable of this optimisation problem whose optimal value corresponds to the DA state analysis. Now, the substitution of the Euclidean norm yields the new 3D-Var cost function:

$$\begin{array}{}\text{(7)}& G_{\mathrm{w}}\left({\mathit{x}}^{\mathrm{a}}\right)={\mathcal{W}}_{\mathrm{2}}^{\mathrm{2}}({\mathit{y}}^{\mathrm{b}},{\mathit{x}}^{\mathrm{a}})+{\mathcal{W}}_{\mathrm{2}}^{\mathrm{2}}({\mathit{y}}^{\mathrm{o}},\mathbf{H}{\mathit{x}}^{\mathrm{a}}),\end{array}$$

where 𝒲₂ is some discretisation of the Wasserstein distance based on the cost defined by the square of the Euclidean distance. Note that this 3D-Var case requires balancing two instances of a Wasserstein-based metric. The analysis state is known as a Wasserstein barycentre (abridged W-barycentre in the following).

Feyeux (2016) and Feyeux et al. (2018) explored the optimisation aspects of this DA problem. However, Feyeux (2016) ultimately pointed to a possible inconsistency in the definition of the DA problem formulated in Eq. (7), where the system is only partially observed (non-trivial H). In the case where the system is fully observed, typically when H is the identity operator, the outcome of the optimisation problem, i.e. the analysis, matches our expectations. However, when the system is partially observed, inconsistencies are observed. Let us see why.

Figure 4a considers the DA problem based on Eq. (7), assuming that only half of the domain is observed. We have solved the corresponding mathematical and numerical problem as raised by Feyeux (2016) and displayed its solution. However, one observes that the mass of the solution concentrates on the observed subdomain and neglects the rest of the domain where the prior mainly concentrates, an outcome suspected by Feyeux (2016). Instead, we would have intuitively preferred a solution close to the one offered by Fig. 4b, whose formulation and numerical solution differ and follow the new approach developed in the present paper (how we obtained this solution will be described in Sect. 2).

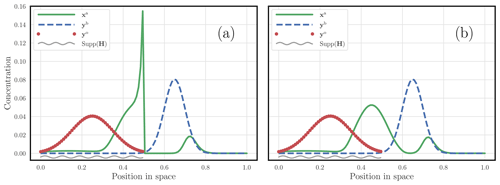
Figure 4 The panels illustrate the analysis of a 3D-Var case that relies on the Wasserstein distance rather than a local metric. The red dots represent the observations, while the dashed blue curve represents the background state. The observations are only focused on the left half of the domain. The solution of the optimisation problem in Eq. (7) is displayed as a solid green curve in panel (a). The solution of the optimisation problem that we will propose in this paper is displayed as a solid green curve in panel (b). The support of the observation is suggested using a wavy grey segment. These states are typically one-dimensional puff pollutant concentrations. They should not be confused with pdfs of a single random variable.

The main caveat of Eq. (7) comes from the fact that the system is only partially observed, as well as the requirement that OT is balanced; i.e. the origin and target densities must have the same mass. This mass balance applies to both OT terms in Eq. (7), between y^b and x^a and between y^o and Hx^a:

$$\begin{array}{}\text{(8)}& \mathrm{m}\left({\mathit{x}}^{\mathrm{a}}\right)=\mathrm{m}\left({\mathit{y}}^{\mathrm{b}}\right),\mathrm{m}\left(\mathbf{H}{\mathit{x}}^{\mathrm{a}}\right)=\mathrm{m}\left({\mathit{y}}^{\mathrm{o}}\right).\end{array}$$

Here, the mass of a vector x∈ℝ^N is defined by

$$\begin{array}{}\text{(9)}& \mathrm{m}\left(\mathit{x}\right)={\mathbf{1}}^{\top }\mathit{x}=\sum _{i=\mathrm{1}}^N{x}_i,\end{array}$$

with 1∈ℝ^N hereafter defined as the vector of entries 1.

Now, if we further assume, for simplicity, that y^b and y^o have the same mass (which is the case in Fig. 4), then

$$\begin{array}{}\text{(10)}& \mathrm{m}\left(\mathbf{H}{\mathit{x}}^{\mathrm{a}}\right)=\mathrm{m}\left({\mathit{y}}^{\mathrm{o}}\right)=\mathrm{m}\left({\mathit{y}}^{\mathrm{b}}\right)=\mathrm{m}\left({\mathit{x}}^{\mathrm{a}}\right).\end{array}$$

As a result, we obtain m(Hx^a)=m(x^a), which is an undesired prior piece of information as to where to find the mass of x^a. Simply put, unless the system is fully observed, this approach amounts to the streetlight effect. This is precisely what happens in Fig. 4a with the undesired concentration of the mass of x^a close to the edge of the observed subdomain.

To overcome this caveat and find a proper alternative to Eq. (7), we need (i) to renounce comparing the fields in observation space (in the observation discrepancy term of the cost function) and (ii) to introduce unbalanced OT (i.e. we need to be able to accommodate states of distinct masses). In the computer science context of pure OT, the latter has been discussed by Chizat et al. (2018). However, our solution differs formally and will be DA-centric.

1.6 Objective and outline

The objective of this paper is to lift the objection of Feyeux (2016) and propose a DA framework based on the Wasserstein distance, thereby offering a consistent way to bridge OT and classical DA. The new formalism will be referred to as hybrid OTDA (hybrid optimal transport data assimilation) in the rest of this paper (or OTDA for brevity). We will focus on the definition of a 3D-Var DA problem and how to obtain its analysis state and the associated analysis error covariance matrix.

At least within the perimeter of this paper, some restrictions apply. Firstly, the physical fields considered in the DA problem are non-negative (concentration of tracer, pollutants, water vapour, hydrometeors, chemical and biogeochemical species, etc.). However, as opposed to Feyeux (2016), the methods of this paper do not require the (possibly noisy) background state y^b and observation y^o to be non-negative. We stress once again that the states of our DA problem are physical fields onto which OT is applied and are not meant to be a pdf of a random variable. Secondly, the observation operator H is assumed to be linear. This is only meant for convenience and to obtain a rigorous correspondence between the primal and dual cost functions of the 3D-Var case. Making this assumption is very common in geophysical DA: H can indeed be seen as the tangent linear of a nonlinear observation operator within the inner loop of a 3D-Var or a 4D-Var case (see, for instance, Courtier, 1997).

The outline of the paper is as follows. After the present introduction (Sect. 1), Sect. 2 discloses our main idea and discusses two mathematical paths to solve the underlying optimisation problem; the first path is enlightening but not necessarily practical, whereas the alternative path is direct and robust but hides some of the concepts behind it. Section 3 provides one- and two-dimensional illustrations of a 3D-Var analysis based on the new hybrid OTDA formalism. These illustrations will show the possibilities and flexibility of the new framework. Importantly, Sect. 3 will also depict classical DA as a limit case of the formalism. In Sect. 4, the second-order analysis, i.e. the uncertainty quantification of the OTDA 3D-Var case, is derived, discussed, and illustrated. Conclusions and perspectives are given in Sect. 5.

2 The main proposal

2.1 Notation and conventions

Non-negative vectors x of size N are called discrete measures; they lie in the orthant ${\mathcal{O}}_N^{+}\stackrel{\Delta }{=}{\mathbb{R}}_{+}^N$. Although most mathematical OT theories work on normalised discrete measures, yielding probability vectors, this assumption will not be needed in this paper. The open subset of ${\mathcal{O}}_N^{+}$ of all the positive discrete measures will be denoted as ${\mathcal{O}}_N^{+,\star }\stackrel{\Delta }{=}{\mathbb{R}}_{+,\star }^N$.

We will distinguish the observations ${\mathit{y}}^{\mathrm{b}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{b}}}$ and ${\mathit{y}}^{\mathrm{o}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{o}}}$ from the observable states ${\mathit{x}}^{\mathrm{b}}\in {\mathcal{O}}_{N_{\mathrm{b}}}^{+}$ and ${\mathit{x}}^{\mathrm{o}}\in {\mathcal{O}}_{N_{\mathrm{o}}}^{+}$. y^b, which corresponds to the first guess of conventional DA, and y^o, which corresponds to the traditional observation vector, are known before solving the 3D-Var problem. These vectors embody all of the information processed in the analysis. By contrast, the observables x^b and x^o, which are related to y^b and y^o, respectively, through an observation operator (the identity for y^b and x^b), are not known a priori. They will be estimated along with the analysis state ${\mathit{x}}^{\mathrm{a}}\in {\mathcal{O}}_{N_{\mathrm{a}}}^{+}$. Note that these vectors may well lie in distinct vector spaces of different dimensions; hence, the introduction of as many dimensions $N_{\mathrm{b}},N_{\mathrm{o}},{\mathcal{N}}_{\mathrm{b}}$, and 𝒩_o. $x_i^{\star }$ can be seen as the value taken by x^⋆ at site ${\mathit{r}}_i^{\star }$, for $\star =\mathrm{b},\mathrm{o}$, and a and $i\in \left[\right[\mathrm{1},N_{\star }\left]\right]$. Mind that the distinction between y^b and x^b and the introduction of x^o are novelties of OTDA compared with classical DA.

Like in classical DA, the vectors y^b and y^o are subject to (prior) errors whose statistics are specified by the likelihoods p(y^b|x^b) and p(y^o|x^o), respectively. Up to constants that do not depend on ${\mathit{x}}^{\mathrm{b}},{\mathit{x}}^{\mathrm{o}},{\mathit{y}}^{\mathrm{b}}$, and y^o, we assume the existence of ζ_b and ζ_o, such that

$$\begin{array}{}\text{(11a)}& {\displaystyle }\ln p\left({\mathit{y}}^{\mathrm{b}}\right|{\mathit{x}}^{\mathrm{b}})\stackrel{\Delta }{=}-{\mathit{\zeta }}_{\mathrm{b}}({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{b}})+\text{cst},\text{(11b)}& {\displaystyle }\ln p\left({\mathit{y}}^{\mathrm{o}}\right|{\mathit{x}}^{\mathrm{o}})\stackrel{\Delta }{=}-{\mathit{\zeta }}_{\mathrm{o}}({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{o}})+\text{cst}.\end{array}$$

Thus, various error statistics can be considered. These errors are hypothesised to be mutually independent. The observation operator $\mathbf{H}:{\mathcal{O}}_{N_{\mathrm{o}}}^{+}\mapsto {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{o}}}$ used in the definition of ζ_o is assumed to be linear. This qualification is for convenience and could be lifted if necessary. It is further assumed that ζ_b and ζ_o are strictly convex functions. This is, for instance, the case if we choose Gaussian error statistics yielding

$$\begin{array}{}\text{(12)}& {\mathit{\zeta }}_{\mathrm{b}}\left({\mathit{e}}_{\mathrm{b}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{∥{\mathit{e}}_{\mathrm{b}}∥}_{{\mathbf{B}}^{-\mathrm{1}}}^{\mathrm{2}},{\mathit{\zeta }}_{\mathrm{o}}\left({\mathit{e}}_{\mathrm{o}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{∥{\mathit{e}}_{\mathrm{o}}∥}_{{\mathbf{R}}^{-\mathrm{1}}}^{\mathrm{2}}.\end{array}$$

Here, ${∥\mathit{e}∥}_{\mathbf{A}}=\sqrt{{\mathit{e}}^{\top }\mathbf{A}\mathit{e}}$. B is the positive definite background error covariance matrix and R is the positive definite observation error covariance matrix. Finally, in the following, the m(⋆) operator will act not only on vectors but also, more generally, on any tensor, and it will return the sum of all of its entries.

2.2 Formalism of discrete optimal transport

To discretise and solve the continuous Kantorovich optimisation problem introduced in Sect. 1.3, we will need two elementary pieces of information about OT. These are not the only techniques that we will leverage, but both represent cornerstones towards a numerical solution to our proposal and, hence, require a proper introduction.

2.2.1 The primal cost function

Let us consider two discrete measures ${\mathit{x}}^{\mathrm{b}}\in {\mathcal{O}}_{N_{\mathrm{b}}}^{+}$ and ${\mathit{x}}^{\mathrm{o}}\in {\mathcal{O}}_{N_{\mathrm{o}}}^{+}$ with the same mass:

$$\begin{array}{}\text{(13)}& m\stackrel{\Delta }{=}\mathrm{m}\left({\mathit{x}}^{\mathrm{b}}\right)=\mathrm{m}\left({\mathit{x}}^{\mathrm{o}}\right).\end{array}$$

For convenience, ${\mathcal{O}}_{\mathrm{b},\mathrm{o}}^{+}$ will be used as an alias for the set ${\mathcal{O}}_{N_{\mathrm{b}}\times N_{\mathrm{o}}}^{+}$. A cost matrix ${\mathbf{C}}_{\mathrm{bo}}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o}}^{+}$ is given. The optimisation problem will be formulated using discrete Kantorovich transference plans ${\mathbf{P}}^{\mathrm{bo}}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o}}^{+}$. The optimal discrete transference plan is given by the minimiser of the following optimisation problem:

$$\begin{array}{}\text{(14a)}& W_{{\mathbf{C}}_{\mathrm{bo}}}({\mathit{x}}^{\mathrm{b}},{\mathit{x}}^{\mathrm{o}})\stackrel{\Delta }{=}\underset{{\mathbf{P}}^{\mathrm{bo}}\in {\mathcal{U}}_{\mathrm{bo}}({\mathit{x}}^{\mathrm{b}},{\mathit{x}}^{\mathrm{o}})}{min}\mathrm{Tr}\left({\mathbf{C}}_{\mathrm{bo}}^{\top }{\mathbf{P}}^{\mathrm{bo}}\right).\end{array}$$

Here, the trace sums up the costs attached to each path, and the set of admissible transference plans is defined by

$$\begin{array}{}\text{(14b)}& {\mathcal{U}}_{\mathrm{bo}}\stackrel{\Delta }{=}\left\{\mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o}}^{+}:\mathbf{P}{\mathbf{1}}_{\mathrm{o}}={\mathit{x}}^{\mathrm{b}},{\mathbf{P}}^{\top }{\mathbf{1}}_{\mathrm{b}}={\mathit{x}}^{\mathrm{o}}\right\},\end{array}$$

which selects the discrete transference plans with the proper marginals. $W_{{\mathbf{C}}_{\mathrm{bo}}}$ could be viewed as a discrete equivalent to the square of the Wasserstein distance ${\mathcal{W}}_{{\mathcal{C}}_{\mathrm{bo}}}^{\mathrm{2}}$ introduced in Eq. (5).

2.2.2 Entropic regularisation

The optimisation problem in Eq. (14) is a linear program that is convex (Peyré and Cuturi, 2019, and references therein). However, it is not generally strictly convex and, hence, does not necessarily exhibit a single minimum. Adding to the difficulty, its cost function (Eq. 14a) is constrained. Entropic regularisation addresses these issues and is used here to lift the constraints and to render the problem strictly convex. In particular, it will force any state vector that is a solution of the problem to be positive. A comprehensive justification is given by Peyré and Cuturi (2019). More precisely, we will use a Kullback–Leibler divergence (KL) regularisation term that is inserted in Eq. (14a),

$$\begin{array}{}\text{(15)}& \mathrm{Tr}\left({\mathbf{C}}_{\mathrm{bo}}^{\top }{\mathbf{P}}^{\mathrm{bo}}\right)\to \mathrm{Tr}\left({\mathbf{C}}_{\mathrm{bo}}^{\top }{\mathbf{P}}^{\mathrm{bo}}\right)+\mathit{\epsilon }\mathcal{K}\left({\mathbf{P}}^{\mathrm{bo}}\right|{\mathit{\nu }}^{\mathrm{bo}}),\end{array}$$

which incorporates some prior transference plan ν^bo and does not require m(P^bo)=1, whereas Peyré and Cuturi (2019) opted for a basic entropy term. The KL term (Boyd and Vandenberghe, 2004) is defined by

$$\begin{array}{}\text{(16)}& \mathcal{K}\left(\mathit{p}\right|\mathit{q})\stackrel{\Delta }{=}\sum _i{p}_i\ln {\displaystyle \frac{p_i}{q_i}}-p_i+q_i.\end{array}$$

It can be checked that the Hessian of the regularised cost function (Eq. 15) is a diagonal matrix of coefficients $\mathit{\epsilon }/P_{ij}^{\mathrm{bo}}\ge \mathit{\epsilon }$ because $\mathrm{0}\le P_{ij}^{\mathrm{bo}}\le \mathrm{1}$, making the problem ε-strongly convex. We choose, for example, ${\mathit{\nu }}^{\mathrm{bo}}={\mathit{x}}^{\mathrm{b}}{\left({\mathit{x}}^{\mathrm{o}}\right)}^{\top }/m$ and ε>0, the latter of which is the regularisation scalar parameter. Note that this particular ν^bo is an admissible transference plan, i.e. it belongs to 𝒰_bo, and can be interpreted as a complete statistical decoupling of the transference plan with respect to the origin and target discrete measures. In the limit $\mathit{\epsilon }\to {\mathrm{0}}^{+}$ of vanishing regularisation, the solution should not depend on the choice of ν^bo. However, the convergence to the solution at finite ε may depend on this choice. The primal cost function augmented with such an entropic regularisation is usually solved numerically with the iterative Sinkhorn algorithm (Sinkhorn, 1964). However, this is not the path followed in this paper, although we have used it as well.

Finally note that the technique to convexify such an optimisation problem with a KL term has been introduced in DA by Bocquet (2009) and Bocquet et al. (2011) following principles of statistical physics.

2.3 From classical data assimilation to hybrid optimal transport data assimilation

Figure 5 is a schematic representation of the flow of information in a classical DA update (and in particular 3D-Var), using the notation introduced above. In this case, the observables x^b and x^o and the analysis state x^a are the same by construction; hence, x^b and x^o are not needed. This diagram, which could also be seen as a Bayesian network, corresponds to the cost function

$$\begin{array}{}\text{(17)}& L_{\mathrm{cl}}\left({\mathit{x}}^{\mathrm{a}}\right)={\mathit{\zeta }}_{\mathrm{b}}({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{a}})+{\mathit{\zeta }}_{\mathrm{o}}({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{a}})\end{array}$$

to be minimised over x^a. Now let us make use of the observables x^b and x^o as new degrees of freedom but bind them by OTs to x^a, using the cost matrices C_ba and C_oa, respectively.

This yields the diagram in Fig. 6, which corresponds to the cost function

$$\begin{array}{ll}{\displaystyle }{L}_{\mathrm{w}}\left({\mathit{x}}^{\mathrm{a}}\right)=& {\displaystyle }\underset{{\mathit{x}}^{\mathrm{b}}\in {\mathcal{O}}_{N_{\mathrm{b}}}^{+}{\mathit{x}}^{\mathrm{o}}\in {\mathcal{O}}_{N_{\mathrm{o}}}^{+}}{min}\mathit{\left\{}{\mathit{\zeta }}_{\mathrm{b}}\right({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{b}})+{\mathit{\zeta }}_{\mathrm{o}}({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{o}})\\ \text{(18)}& {\displaystyle }& {\displaystyle }+W_{{\mathbf{C}}_{\mathrm{ba}}}({\mathit{x}}^{\mathrm{b}},{\mathit{x}}^{\mathrm{a}})+W_{{\mathbf{C}}_{\mathrm{oa}}}({\mathit{x}}^{\mathrm{o}},{\mathit{x}}^{\mathrm{a}})\mathit{\}}.\end{array}$$

It must be minimised over x^a, yielding an analysis state x^a; this analysis state can also be seen as the W-barycentre between x^b and x^o. Note that x^b and x^o are discrete measures of unknown mass. For the optimisation problem, they lie in ${\mathcal{O}}_{N_{\mathrm{b}}}^{+}$ and ${\mathcal{O}}_{N_{\mathrm{o}}}^{+}$, respectively.

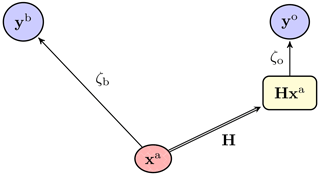
Figure 5 A diagrammatic representation of the classical 3D-Var update, with the observations y^b (the first guess) and y^o (the observation vector), the analysis state x^a, and the observed analysis Hx^a. A double-line arrow represents a deterministic map, whereas a single-line arrow represents a statistical binding between the origin and the target.

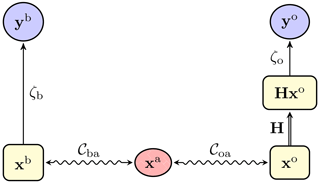
Figure 6 A diagrammatic representation of the hybrid OTDA 3D-Var update, with the observations y^b (the first guess) and y^o (the observation vector); the observables x^b and x^o; and x^a, which is the W-barycentre. A double-line arrow represents a deterministic map, a single-line arrow represents a statistical binding between the origin and the target, and a wavy line represents the weaker bindings of x^b with x^a and x^o with x^a through OTs. This diagram can be seen as an unfolding of that in Fig. 5.

Moving from Eq. (17) to Eq. (18) following the principles and guidance of the introductory Sect. 1.4 is empirical, although no more than in Ning et al. (2014) and Feyeux (2016). Showing the merits of this move from Eq. (17) to Eq. (18) is the goal of the present paper. As opposed to Feyeux et al. (2018), it can deal with sparse and noisy observations, i.e. non-trivial H. We will show that classical DA is embedded in this generalisation. Moreover, the merits of the new cost function will be a posteriori qualitatively supported by the outcome of the numerical experiments (to the expert's eyes), which improve over previous formalism's outcomes. We would like to point out that we have also developed a consistent probabilistic and Bayesian formalism fully supporting the introduction of Eq. (18). However, we felt that the derivation was too long and technical for this paper and would not be helpful in the exploration of the direct consequences of Eq. (18).

We call Eq. (18) a high-level primal cost function because the metrics $W_{{\mathbf{C}}_{\mathrm{ba}}}$ and $W_{{\mathbf{C}}_{\mathrm{oa}}}$ have not yet been replaced by their transference plan expression, as opposed to, for example, Eq. (14a). Passing to a lower-level primal cost function would require expanding Eq. (18) using Eq. (14a) twice.

In the subsequent two subsections, we will investigate two pathways to solve the optimisation problem in Eq. (18). The first path (Sect. 2.4) unveils some of the key concepts behind its solution and partially disentangles the classical DA part from the W-barycentre part of the full analysis. This approach is enlightening but not necessarily practical. The second path is an alternative which is direct and robust but hides some of the fundamental principles underlying the solution. The busy reader could skip directly to the latter (i.e. Sect. 2.5).

2.4 Decomposition of the optimisation problem and effective cost metric

In this section, key ideas behind the minimisation of Eq. (18) are sketched and discussed. The level of mathematical rigour of this section is that of casual methodological DA in the geoscience literature. However, we stress that all of the algorithms discussed here have been successfully numerically tested on various configurations. The solution of Eq. (18) presented in this section is not necessarily robust, but it is enlightening and, hence, worth discussing.

Repeated contravariant indices – meaning the same tensor index is present as the upper and lower index – in tensor expressions will be understood as summed over, following Einstein's convention.

2.4.1 Dual formulation of the primal problem

One way, although not the only one, to write the explicit primal problem associated with Eq. (18) is through the use of a gluing transference plan ${\mathbf{P}}^{\mathrm{boa}}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o},\mathrm{a}}^{+}$, where ${\mathcal{O}}_{\mathrm{b},\mathrm{o},\mathrm{a}}^{+}={\mathbb{R}}_{+}^{N_{\mathrm{b}}{N}_{\mathrm{o}}{N}_{\mathrm{a}}}$ (see pp. 11–12 of Vilani, 2009). ${\mathbf{P}}^{\mathrm{boa}}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o},\mathrm{a}}^{+}$ is a 3-tensor whose marginals are x^b, x^o, and x^a and that glues the transference plans P^ba between x^b and x^a and P^oa between x^o and x^a:

$$\begin{array}{}\text{(19a)}& {\displaystyle }\mathcal{L}=\underset{{\mathit{x}}^{\mathrm{a}}\in {\mathcal{O}}_{\mathrm{a}}^{+}}{min}{L}_{\mathrm{w}}\left({\mathit{x}}^{\mathrm{a}}\right)\text{(19b)}& {\displaystyle }\begin{array}{rl}& =\underset{{\mathit{x}}^{\mathrm{b}}\in {\mathcal{O}}_{\mathrm{b}}^{+}{\mathit{x}}^{\mathrm{o}}\in {\mathcal{O}}_{\mathrm{o}}^{+}{\mathit{x}}^{\mathrm{a}}\in {\mathcal{O}}_{\mathrm{a}}^{+}}{min}\left[{\mathit{\zeta }}_{\mathrm{b}}\right({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{b}})+{\mathit{\zeta }}_{\mathrm{o}}({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{o}})\\ & +\underset{\mathbf{P}\in {\mathcal{U}}_{\mathrm{boa}}}{min}\left\{P_{ijk}{C}_{\mathrm{ba}}^{ik}+P_{ijk}{C}_{\mathrm{oa}}^{jk}\right\}].\end{array}\end{array}$$

Here, the admissible set of (glued) transference plans, the set of all 3-tensors of non-negative entries whose marginals are x^b, x^o, and x^a, is defined by

$$\begin{array}{}\text{(19c)}& \begin{array}{rl}{\mathcal{U}}_{\mathrm{boa}}\stackrel{\Delta }{=}\mathit{\{}& \mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o},\mathrm{a}}^{+}:\forall i,P_{ijk}{\mathrm{1}}_{\mathrm{o}}^j{\mathrm{1}}_{\mathrm{a}}^k=x_i^{\mathrm{b}},\\ & \forall j,P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{a}}^k=x_j^{\mathrm{o}},\forall k,P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j=x_k^{\mathrm{a}}\mathit{\}}.\end{array}\end{array}$$

Due to the hardly scalable dimensionality of the primal problem, based on either a 3-tensor or a couple of 2-tensors, we wish to derive a dual problem equivalent to the primal one, using Lagrange multipliers to lift the constraints with (as will be checked later) a significantly smaller dimensionality.

This leads to a series of transformations of the problem ℒ, from a Lagrangian to a dual cost function, which is reported in Appendix A for the mathematically inclined reader. The outcome is a dual problem which reads

$$\begin{array}{}\text{(20a)}& \begin{array}{rl}{\mathcal{L}}^{\ast }=\underset{({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}})\in {\mathcal{U}}_{\mathrm{bo}}^{\ast }({\mathbf{C}}_{\mathrm{ba}},{\mathbf{C}}_{\mathrm{oa}},\mathbf{H})}{max}\mathit{\{}& {\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{y}}^{\mathrm{b}}+{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{y}}^{\mathrm{o}}\\ & -{\mathit{\zeta }}_{\mathrm{b}}^{\ast }\left({\mathit{f}}_{\mathrm{b}}\right)-{\mathit{\zeta }}_{\mathrm{o}}^{\ast }\left({\mathit{f}}_{\mathrm{o}}\right)\mathit{\}},\end{array}\end{array}$$

where the ∗ symbol refers to dual and where the polyhedron ${\mathcal{U}}_{\mathrm{bo}}^{\ast }({\mathbf{C}}_{\mathrm{ba}},{\mathbf{C}}_{\mathrm{oa}},\mathbf{H})$ is defined by

$$\begin{array}{}\text{(20b)}& \begin{array}{rl}{\mathcal{U}}_{\mathrm{bo}}^{\ast }({\mathbf{C}}_{\mathrm{ba}},& {\mathbf{C}}_{\mathrm{oa}},\mathbf{H}\left)\stackrel{\Delta }{=}\mathit{\right\{}{\mathit{f}}_{\mathrm{b}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{b}}},{\mathit{f}}_{\mathrm{o}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{o}}}:\\ & \forall i,j,k,f_{\mathrm{b}}^i+f_{\mathrm{o}}^l{H}_l^j\le C_{\mathrm{ba}}^{ik}+C_{\mathrm{oa}}^{jk}\mathit{\}}.\end{array}\end{array}$$

In Eq. (20), the maps ${\mathit{\zeta }}_{\mathrm{b}}^{\ast }$ and ${\mathit{\zeta }}_{\mathrm{o}}^{\ast }$ are the Legendre–Fenchel transforms of the maps ζ_b and ζ_o, respectively. Let us recall that the Legendre–Fenchel transform $\mathit{f}\mapsto {\mathit{\zeta }}^{\ast }\left(\mathit{f}\right)$ of the map e↦ζ(e) is defined by ${\mathit{\zeta }}^{\ast }\left(\mathit{f}\right)={\sup }_{\mathit{e}}\left\{{\mathit{f}}^{\top }\mathit{e}-\mathit{\zeta }\left(\mathit{e}\right)\right\}$. For instance, in the case of Gaussian error statistics (as in Eq. 12), these transforms are given by

$$\begin{array}{}\text{(21)}& {\mathit{\zeta }}_{\mathrm{b}}^{\ast }\left({\mathit{f}}_{\mathrm{b}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{∥{\mathit{f}}_{\mathrm{b}}∥}_{\mathbf{B}}^{\mathrm{2}},{\mathit{\zeta }}_{\mathrm{o}}^{\ast }\left({\mathit{f}}_{\mathrm{o}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{∥{\mathit{f}}_{\mathrm{o}}∥}_{\mathbf{R}}^{\mathrm{2}}.\end{array}$$

Note that, in this section, we do not add the entropic regularisation to the cost functions for the sake of conciseness and because it does not play a role in the key ideas developed in this section; however, it would likely be added and employed in numerical applications.

2.4.2 Decomposition of the dual problem

These transformations allow us to trade the primal for the dual problem. Due to the fact that there are N_a constraints indexed by $k\in \left[\right[\mathrm{1},N_{\mathrm{a}}\left]\right]$ for each f_b and f_o pair in ${\mathcal{U}}_{\mathrm{bo}}^{\ast }$ and that the tightest of these constraints can account for the others, the problem in Eq. (20) should be equivalent to

$$\begin{array}{}\text{(22a)}& \begin{array}{rl}{\mathcal{L}}^{\ast }& =\underset{({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}})\in {\mathcal{U}}_{\mathrm{bo}}^{\ast }({\mathbf{C}}_{\mathrm{bo}},\mathbf{H})}{max}\\ & \left\{{\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{y}}^{\mathrm{b}}+{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{y}}^{\mathrm{o}}-{\mathit{\zeta }}_{\mathrm{b}}^{\ast }\left({\mathit{f}}_{\mathrm{b}}\right)-{\mathit{\zeta }}_{\mathrm{o}}^{\ast }\left({\mathit{f}}_{\mathrm{o}}\right)\right\},\end{array}\end{array}$$

where the polyhedron ${\mathcal{U}}_{\mathrm{bo}}^{\ast }({\mathbf{C}}_{\mathrm{bo}},\mathbf{H})$ is defined by

$$\begin{array}{}\text{(22b)}& \begin{array}{rl}{\mathcal{U}}_{\mathrm{bo}}^{\ast }({\mathbf{C}}_{\mathrm{bo}},\mathbf{H})\stackrel{\Delta }{=}\mathit{\{}& {\mathit{f}}_{\mathrm{b}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{b}}},{\mathit{f}}_{\mathrm{o}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{o}}}:\\ & \forall i,j,f_{\mathrm{b}}^i+f_{\mathrm{o}}^l{H}_l^j\le C_{\mathrm{bo}}^{ij}\mathit{\}}\end{array}\end{array}$$

and the effective cost metric C_bo is given (in the absence of entropic regularisation) by

$$\begin{array}{}\text{(22c)}& [{\mathbf{C}}_{\mathrm{bo}}{]}_{ij}\stackrel{\Delta }{=}\underset{k}{min}\left\{[{\mathbf{C}}_{\mathrm{ba}}{]}_{ik}+[{\mathbf{C}}_{\mathrm{oa}}{]}_{jk}\right\}.\end{array}$$

According to Eq. (22c), this effective cost is given by the cost of the cheapest path(s), which is intuitive. The optimal transference glued plan, P, can be connected to the optimal transference plan P^bo between x^b and x^o with the cost C_bo in Eq. (22c), by marginalising on the intermediate density, i.e. the W-barycentre,

$$\begin{array}{}\text{(23)}& P_{ij}^{\mathrm{bo}}=P_{ijk}{\mathrm{1}}_{\mathrm{a}}^k.\end{array}$$

The solution for the analysis state x^a is given by

$$\begin{array}{}\text{(24)}& x_k^{\mathrm{a}}=P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j,\end{array}$$

by the definition of the marginals of the gluing transference plan P (Eq. 19c). However, we do not have direct access to the optimal gluing P from the dual problem (Eq. 22). This will be made simpler later on when adding the entropic regularisation to the problem.

For now, let us find an alternative solution bypassing the need for the gluing P and define the map

$$\begin{array}{ll}{\displaystyle }{\mathit{\kappa }}^{\mathrm{bo}}:& {\displaystyle }\left[\right[\mathrm{1},N_{\mathrm{b}}\left]\right]\times \left[\right[\mathrm{1},N_{\mathrm{o}}\left]\right]\mapsto \mathcal{P}\left(\right[[\mathrm{1},N_{\mathrm{a}}]\left]\right)\\ \text{(25)}& {\displaystyle }& {\displaystyle }(i,j)\mapsto {\mathit{\kappa }}_{ij}^{\mathrm{bo}}=\underset{k}{\arg \min }\left(C_{\mathrm{ba}}^{ik}+C_{\mathrm{oa}}^{jk}\right),\end{array}$$

where 𝒫(S) is defined as the set of all subsets of S. The set ${\mathit{\kappa }}_{ij}^{\mathrm{bo}}$ lists all of the indices k that are relays to the transport in between the sites corresponding to index i and index j. That is why the W-barycentre can be obtained from P^bo:

$$\begin{array}{}\text{(26)}& x_k^{\mathrm{a}}=P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j=\sum _{ij}{P}_{ij}^{\mathrm{bo}}{\mathit{\delta }}_{k\in {\mathit{\kappa }}_{ij}^{\mathrm{bo}}}.\end{array}$$

In the next section, we will show how to estimate P^bo using entropic regularisation and, hence, leverage Eq. (26) to compute x^a. κ^bo is reminiscent of the so-called McCann interpolant in OT theory, as it is only related to the OT between x^b and x^o, bypassing x^a and, hence, the transference plan P^bo. Please refer to Remark 7.1 by Peyré and Cuturi (2019) and to Gangbo and McCann (1996) for a description of the McCann interpolant, even when there is no Monge map. This suggests that the analysis x^a is not an interpolation of x^b and x^o in the space of values, as for classical DA, but along a geodesic in a Riemannian space built on a metric derived from the Wasserstein distance.

Nonetheless, the above derivation shows that we can trade a W-barycentre problem characterised by a couple of OT problems for a single OT problem defined by an effective metric C_bo. This principle is schematically illustrated in Fig. 7.

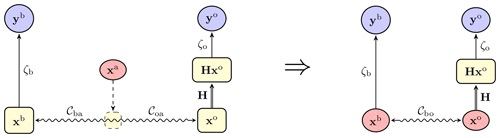
Figure 7 Trading a full hybrid OTDA problem, characterised by a W-barycentre defined by the cost metrics C_ba and C_oa, with a simplified hybrid OTDA problem, characterised by a single OT problem defined by an effective cost metric C_bo.

This suggests a simpler two-step algorithm, where the steps consist of the following: (i) solving a hybrid OTDA problem but with a single OT problem under an effective cost metric, which yields the analysed observables x^b and x^o, and (ii) computing the W-barycentre of x^b and x^o. To avoid making an overly large detour, the derivation of this algorithm is presented in Appendix B.

2.4.3 Classical data assimilation as a particular case

The primal problem (Eq. 17) of classical DA reads as follows:

$$\begin{array}{}\text{(27)}& {\mathcal{L}}_{\mathrm{cl}}=\underset{{\mathit{x}}^{\mathrm{a}}\in {\mathcal{O}}_{N_{\mathrm{a}}}^{+}}{min}\left\{{\mathit{\zeta }}_{\mathrm{b}}({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{a}})+{\mathit{\zeta }}_{\mathrm{o}}({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{a}})\right\}.\end{array}$$

Let us see how the OTDA formalism in Eq. (22) can account for classical DA. In the context of classical DA, the observable spaces for x^b, x^o, and x^a are assumed to be the same by construction. Let us then define the cost matrices

$$\begin{array}{}\text{(28)}& {\left[{\mathbf{C}}_{\mathrm{ba}}^{\mathrm{\infty }}\right]}_{ij}\stackrel{\Delta }{=}{\left[{\mathbf{C}}_{\mathrm{oa}}^{\mathrm{\infty }}\right]}_{ij}\stackrel{\Delta }{=}\left\{\begin{array}{ccc}\mathrm{0}& \text{if}& i=j\\ +\mathrm{\infty }& \text{if}& i\ne j\end{array}\right.;\end{array}$$

i.e. it is assumed that the cost of moving masses is as large as it can be. Looking back at Eq. (19) but with these costs, it is clear that, in order to avoid the primal cost function being +∞, the transference plan P_ijk must always be 0 unless $i=j=k$. However, this implies, from the definition of 𝒰_boa, that the observables coincide, ${\mathit{x}}^{\mathrm{b}}={\mathit{x}}^{\mathrm{o}}={\mathit{x}}^{\mathrm{a}}$, and that their mass is given by m(P). In this limit where the specific cost matrices are equal to ${\mathbf{C}}_{\mathrm{ba}}^{\mathrm{\infty }}$ and ${\mathbf{C}}_{\mathrm{oa}}^{\mathrm{\infty }}$, the OTDA primal problem become mathematically equivalent to classical DA. Hence, classical DA is a limit case of OTDA. Note that, from its definition (Eq. 22c), the effective cost C_bo obtained from ${\mathbf{C}}_{\mathrm{ba}}^{\mathrm{\infty }}$ and ${\mathbf{C}}_{\mathrm{oa}}^{\mathrm{\infty }}$ coincides with ${\mathbf{C}}_{\mathrm{bo}}^{\mathrm{\infty }}\stackrel{\Delta }{=}{\mathbf{C}}_{\mathrm{ba}}^{\mathrm{\infty }}={\mathbf{C}}_{\mathrm{oa}}^{\mathrm{\infty }}$.

2.5 A direct algorithmic solution

The two-step approach of Sect. 2.4 has merit in that it connects to the traditional W-barycentre problem, by first estimating x^b and x^o, and later computes the W-barycentre in between both states. It also suggests the existence of the effective cost metric of the problem. However, going through its consecutive steps may not be necessary for pure computational purposes. Here, we describe a direct approach that yields the analysis of the OTDA problem. It is less enlightening, but it is practical and will be used in the subsequent illustrations of the present paper.

An alternative formulation to the primal problem in Eq. (19) relies on two transference plans P^ba and P^oa corresponding to the two transports of the underlying W-barycentre problem, instead of the gluing one. Moreover, entropic regularisation is now enforced via 𝒦(P^ba|ν^ba) and 𝒦(P^oa|ν^oa). The corresponding optimisation problem reads as follows:

$$\begin{array}{ll}{\displaystyle }\mathcal{L}=& {\displaystyle }\underset{{\mathit{x}}^{\mathrm{b}}\in {\mathcal{O}}_{\mathrm{b}}^{+}{\mathit{x}}^{\mathrm{o}}\in {\mathcal{O}}_{\mathrm{o}}^{+}{\mathit{x}}^{\mathrm{a}}\in {\mathcal{O}}_{\mathrm{a}}^{+}}{min}\left[{\mathit{\zeta }}_{\mathrm{b}}\right({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{b}})+{\mathit{\zeta }}_{\mathrm{o}}({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{o}})\\ {\displaystyle }& {\displaystyle }+\underset{{\mathbf{P}}^{\mathrm{ba}}\in {\mathcal{U}}_{\mathrm{ba}}{\mathbf{P}}^{\mathrm{oa}}\in {\mathcal{U}}_{\mathrm{oa}}}{min}\mathit{\left\{}\mathit{\epsilon }\mathcal{K}\right({\mathbf{P}}^{\mathrm{ba}}\left|{\mathit{\nu }}^{\mathrm{ba}}\right)+\mathit{\epsilon }\mathcal{K}\left({\mathbf{P}}^{\mathrm{oa}}\right|{\mathit{\nu }}^{\mathrm{oa}})\\ \text{(29a)}& {\displaystyle }& {\displaystyle }+P_{ik}^{\mathrm{ba}}{C}_{\mathrm{ba}}^{ik}+P_{jk}^{\mathrm{oa}}{C}_{\mathrm{oa}}^{jk}\mathit{\left\}}\right],\end{array}$$

where the admissible sets of the respective transference plans P^ba and P^oa are defined by

$$\begin{array}{}\text{(29b)}& {\displaystyle }{\mathcal{U}}_{\mathrm{ba}}& {\displaystyle }\stackrel{\Delta }{=}\left\{\mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{a}}^{+}:\mathbf{P}{\mathbf{1}}_{\mathrm{a}}={\mathit{x}}^{\mathrm{b}},{\mathbf{P}}^{\top }{\mathbf{1}}_{\mathrm{b}}={\mathit{x}}^{\mathrm{a}}\right\},\text{(29c)}& {\displaystyle }{\mathcal{U}}_{\mathrm{oa}}& {\displaystyle }\stackrel{\Delta }{=}\left\{\mathbf{P}\in {\mathcal{O}}_{\mathrm{o},\mathrm{a}}^{+}:\mathbf{P}{\mathbf{1}}_{\mathrm{a}}={\mathit{x}}^{\mathrm{o}},{\mathbf{P}}^{\top }{\mathbf{1}}_{\mathrm{b}}={\mathit{x}}^{\mathrm{a}}\right\}.\end{array}$$

Following the same type of derivation as reported in the previous sections and Appendix B, the corresponding dual problem to be minimised is obtained as follows:

$$\begin{array}{}\text{(30a)}& {\mathcal{J}}_{\mathit{\epsilon }}^{\ast }=\underset{{\mathit{f}}_{\mathrm{b}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{b}}}{\mathit{f}}_{\mathrm{o}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{o}}}{\mathit{f}}_{\mathrm{a}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{a}}}}{min}{J}_{\mathit{\epsilon }}^{\ast }({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}},{\mathit{f}}_{\mathrm{a}}).\end{array}$$

Here, discarding the constant $-\mathit{\epsilon }\mathrm{m}\left({\mathit{\nu }}^{\mathrm{ba}}\right)-\mathit{\epsilon }\mathrm{m}\left({\mathit{\nu }}^{\mathrm{oa}}\right)$, the associated regularised Lagrangian is

$$\begin{array}{}\text{(30b)}& \begin{array}{rl}{J}_{\mathit{\epsilon }}^{\ast }({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}},{\mathit{f}}_{\mathrm{a}})=& \mathit{\epsilon }{Z}_{\mathit{\epsilon }}^{\mathrm{ba}}({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{a}})+\mathit{\epsilon }{Z}_{\mathit{\epsilon }}^{\mathrm{oa}}({\mathit{f}}_{\mathrm{o}},{\mathit{f}}_{\mathrm{a}})\\ & +{\mathit{\zeta }}_{\mathrm{b}}^{\ast }\left({\mathit{f}}_{\mathrm{b}}\right)+{\mathit{\zeta }}_{\mathrm{o}}^{\ast }\left({\mathit{f}}_{\mathrm{o}}\right)-{\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{y}}^{\mathrm{b}}-{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{y}}^{\mathrm{o}},\end{array}\end{array}$$

with a partition function associated with each transport:

$$\begin{array}{}\text{(30c)}& {\displaystyle }{Z}_{\mathit{\epsilon }}^{\mathrm{ba}}\stackrel{\Delta }{=}\sum _{ik}{P}_{ik}^{\mathrm{ba}},\text{(30d)}& {\displaystyle }{Z}_{\mathit{\epsilon }}^{\mathrm{oa}}\stackrel{\Delta }{=}\sum _{jk}{P}_{jk}^{\mathrm{oa}},\end{array}$$

where

$$\begin{array}{}\text{(30e)}& {\displaystyle }{P}_{ik}^{\mathrm{ba}}={\mathit{\nu }}_{ik}^{\mathrm{ba}}{e}^{\left(f_{\mathrm{b}}^i+f_{\mathrm{a}}^k-C_{\mathrm{ba}}^{ik}\right)/\mathit{\epsilon }},\text{(30f)}& {\displaystyle }{P}_{jk}^{\mathrm{oa}}={\mathit{\nu }}_{jk}^{\mathrm{oa}}{e}^{\left(f_{\mathrm{o}}^l{H}_l^j-f_{\mathrm{a}}^k-C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }}.\end{array}$$

It turns out that the optimal f_a can be obtained analytically as a function of f_b and f_o, which we checked makes the optimisation numerically more efficient and robust. Indeed, let us introduce ${\mathit{\psi }}_k\stackrel{\Delta }{=}{e}^{f_{\mathrm{a}}^k/\mathit{\epsilon }}$. We could optimise $J_{\mathit{\epsilon }}^{\ast }({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}},{\mathit{f}}_{\mathrm{a}}=\mathit{\epsilon }\ln \mathit{\psi })$ on ψ:

$$\begin{array}{}\text{(31a)}& {\displaystyle }\mathrm{0}=& {\displaystyle }{\partial }_{{\mathit{\psi }}_k}{J}_{\mathit{\epsilon }}^{\ast }({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}},{\mathit{f}}_{\mathrm{a}})\text{(31b)}& {\displaystyle }=& {\displaystyle }\sum _i{\mathit{\nu }}_{ik}^{\mathrm{ba}}{e}^{\left(f_{\mathrm{b}}^i-C_{\mathrm{ba}}^{ik}\right)/\mathit{\epsilon }}-{\displaystyle \frac{\mathrm{1}}{{\mathit{\psi }}_k^{\mathrm{2}}}}\sum _j{\mathit{\nu }}_{jk}^{\mathrm{oa}}{e}^{\left(f_{\mathrm{o}}^l{H}_l^j-C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }},\end{array}$$

yielding the solution

$$\begin{array}{}\text{(32a)}& {\displaystyle }{\mathit{\psi }}_k^{\mathrm{2}}& {\displaystyle }={\displaystyle \frac{Z_{\mathit{\epsilon },k}^{\mathrm{oa}}}{Z_{\mathit{\epsilon },k}^{\mathrm{ba}}}},\text{(32b)}& {\displaystyle }{Z}_{\mathit{\epsilon },k}^{\mathrm{oa}}& {\displaystyle }\stackrel{\Delta }{=}\sum _j{\mathit{\nu }}_{jk}^{\mathrm{oa}}{e}^{\left(f_{\mathrm{o}}^l{H}_l^j-C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }},\text{(32c)}& {\displaystyle }{Z}_{\mathit{\epsilon },k}^{\mathrm{ba}}& {\displaystyle }\stackrel{\Delta }{=}\sum _i{\mathit{\nu }}_{ik}^{\mathrm{ba}}{e}^{\left(f_{\mathrm{b}}^i-C_{\mathrm{ba}}^{ik}\right)/\mathit{\epsilon }}.\end{array}$$

Up to irrelevant constants, the resulting effective cost function using the optimal ψ_k is

$$\begin{array}{}\text{(33)}& \begin{array}{rl}{J}_{\mathit{\epsilon }}^{\ast }({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}})=& \mathrm{2}\mathit{\epsilon }\sum _k\sqrt{Z_{\mathit{\epsilon },k}^{\mathrm{ba}}{Z}_{\mathit{\epsilon },k}^{\mathrm{oa}}}+{\mathit{\zeta }}_{\mathrm{b}}^{\ast }\left({\mathit{f}}_{\mathrm{b}}\right)+{\mathit{\zeta }}_{\mathrm{o}}^{\ast }\left({\mathit{f}}_{\mathrm{o}}\right)\\ & -{\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{y}}^{\mathrm{b}}-{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{y}}^{\mathrm{o}}.\end{array}\end{array}$$

Now, the optimal W-barycentre x^a is given by either $x_k^{\mathrm{a}}=P_{ik}^{\mathrm{ba}}{\mathrm{1}}_{\mathrm{b}}^i$ or $x_k^{\mathrm{a}}=P_{jk}^{\mathrm{oa}}{\mathrm{1}}_{\mathrm{o}}^j$, i.e.

$$\begin{array}{}\text{(34)}& x_k^{\mathrm{a}}={\mathit{\psi }}_k{Z}_{\mathit{\epsilon },k}^{\mathrm{ba}}={\displaystyle \frac{\mathrm{1}}{{\mathit{\psi }}_k}}{Z}_{\mathit{\epsilon },k}^{\mathrm{oa}},\end{array}$$

from which we can infer the ψ_k-free expression

$$\begin{array}{}\text{(35)}& x_k^{\mathrm{a}}=\sqrt{Z_{\mathit{\epsilon },k}^{\mathrm{ba}}{Z}_{\mathit{\epsilon },k}^{\mathrm{oa}}}.\end{array}$$

It is also useful to retrieve the optimal value of f_a and obtain

$$\begin{array}{}\text{(36)}& f_{\mathrm{a}}^k=\mathit{\epsilon }\ln {\mathit{\psi }}_k={\displaystyle \frac{\mathit{\epsilon }}{\mathrm{2}}}\ln \left({\displaystyle \frac{Z_{\mathit{\epsilon },k}^{\mathrm{oa}}}{Z_{\mathit{\epsilon },k}^{\mathrm{ba}}}}\right),\end{array}$$

so that we can compute the other two analysed observables, x^b and x^o, using

$$\begin{array}{}\text{(37a)}& {\displaystyle }\begin{array}{rl}{x}_i^{\mathrm{b}}& =P_{ik}^{\mathrm{ba}}{\mathrm{1}}_{\mathrm{a}}^k=\sum _k{\mathit{\psi }}_k{\mathit{\nu }}_{ik}^{\mathrm{ba}}{e}^{\left(f_{\mathrm{b}}^i-C_{\mathrm{ba}}^{ik}\right)/\mathit{\epsilon }}\\ & =e^{f_{\mathrm{b}}^i/\mathit{\epsilon }}\sum _k{\mathit{\nu }}_{ik}^{\mathrm{ba}}{e}^{\left(f_{\mathrm{a}}^k-C_{\mathrm{ba}}^{ik}\right)/\mathit{\epsilon }},\end{array}\text{(37b)}& {\displaystyle }\begin{array}{rl}{x}_j^{\mathrm{o}}& =P_{jk}^{\mathrm{oa}}{\mathrm{1}}_{\mathrm{a}}^k=\sum _k{\displaystyle \frac{\mathrm{1}}{{\mathit{\psi }}_k}}{\mathit{\nu }}_{jk}^{\mathrm{oa}}{e}^{\left(f_{\mathrm{o}}^l{H}_l^j-C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }}\\ & =e^{\left(f_{\mathrm{o}}^l{H}_l^j\right)/\mathit{\epsilon }}\sum _k{\mathit{\nu }}_{jk}^{\mathrm{oa}}{e}^{\left(-f_{\mathrm{a}}^k-C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }}.\end{array}\end{array}$$

Note that most of these expressions can be assessed in a robust way in the log domain. For instance, in practice, we use, equivalently to Eqs. (35) and (37),

$$\begin{array}{ll}{\displaystyle }\mathit{\epsilon }\ln x_k^{\mathrm{a}}=& {\displaystyle \frac{\mathit{\epsilon }}{\mathrm{2}}}\ln \sum _i{\mathit{\nu }}_{ik}^{\mathrm{ba}}{e}^{\left(f_{\mathrm{b}}^i-C_{\mathrm{ba}}^{ik}\right)/\mathit{\epsilon }}\\ \text{(38a)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\mathit{\epsilon }}{\mathrm{2}}}\ln \sum _j{\mathit{\nu }}_{jk}^{\mathrm{oa}}{e}^{\left(f_{\mathrm{o}}^l{H}_l^j-C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }},\text{(38b)}& {\displaystyle }\mathit{\epsilon }\ln x_i^{\mathrm{b}}=& {\displaystyle }{f}_{\mathrm{b}}^i+\mathit{\epsilon }\ln \sum _k{\mathit{\nu }}_{ik}^{\mathrm{ba}}{e}^{\left(f_{\mathrm{a}}^k-C_{\mathrm{ba}}^{ik}\right)/\mathit{\epsilon }},\text{(38c)}& {\displaystyle }\mathit{\epsilon }\ln x_j^{\mathrm{o}}=& {\displaystyle }{f}_{\mathrm{o}}^l{H}_l^j+\mathit{\epsilon }\ln \sum _k{\mathit{\nu }}_{jk}^{\mathrm{oa}}{e}^{\left(-f_{\mathrm{a}}^k-C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }}.\end{array}$$

3 Numerical illustrations

In this section, we showcase a selection of OTDA 3D-Var analyses. These are meant to stress the versatility of the formalism and the diverse solutions it offers, with significantly more degrees of freedom than in classical DA. The OTDA state analysis is carried out using the process in Sect. 2.5 and its formulas. Unless specifically discussed, entropic regularisation is used with $\mathit{\epsilon }={\mathrm{10}}^{-\mathrm{3}}$. The dual cost function in Eq. (33) is minimised using the quasi-Newton method L-BFGS-B (Liu and Nocedal, 1989), which yields the optimal f_b and f_o. Then, Eq. (38) is employed to compute x^b, x^o, and x^a.

3.1 One-dimensional examples

Considering the case in which the physical space of the fields is one-dimensional, we build bell-shaped observations y^b and y^o, related to an observable space of size $N_{\mathrm{b}}=N_{\mathrm{o}}=N_{\mathrm{a}}={\mathrm{10}}^{\mathrm{2}}$ shared by x^b, x^o, and x^a. As y^b is a fully observed instance of x^b, we have ${\mathcal{N}}_{\mathrm{b}}=N_{\mathrm{b}}={\mathrm{10}}^{\mathrm{2}}$, while 𝒩_o may differ from N_o depending on the definition of the observation operator H. We choose (Gaussian statistics)

$$\begin{array}{}\text{(39)}& {\mathit{\zeta }}_{\mathrm{b}}\left({\mathit{e}}_{\mathrm{b}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}}}{∥{\mathit{e}}_{\mathrm{b}}∥}^{\mathrm{2}},{\mathit{\zeta }}_{\mathrm{b}}\left({\mathit{e}}_{\mathrm{o}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\sigma }}_{\mathrm{o}}^{\mathrm{2}}}}{∥{\mathit{e}}_{\mathrm{o}}∥}^{\mathrm{2}}.\end{array}$$

Here, ${\mathit{\sigma }}_{\mathrm{b}}={\mathit{\sigma }}_{\mathrm{o}}={\mathrm{10}}^{-\mathrm{2}}$. The states are discretised over the interval [0,1] at sites/grid cells $r_i^{\star }=(i-\frac{\mathrm{1}}{\mathrm{2}})/N_{\star }$ for $i\in \left[\right[\mathrm{1},N_{\star }\left]\right]$, with $\star =\mathrm{b},\mathrm{o}$, and a. Unless otherwise specified, the cost metric has a quadratic dependence on the distance between sites, i.e. $[{\mathbf{C}}_{\mathrm{ba}}{]}_{ik}=|r_i^{\mathrm{b}}-r_k^{\mathrm{a}}{|}^{\mathrm{2}}$ and $[{\mathbf{C}}_{\mathrm{oa}}{]}_{jk}=|r_j^{\mathrm{o}}-r_k^{\mathrm{a}}{|}^{\mathrm{2}}$. This is our reference set-up. The observation operator and the mass of the observations y^b and y^o will be specified for each experiment.

We consider four experiments in which we choose to vary key parameters in the OTDA set-up.

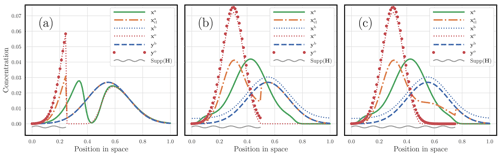
3.1.1 Varying the imbalance of the observation states

In the first experiment, the system is fully observed with H=I. We choose m(y^b)=1 and the mass of y^o to be in the set $\mathrm{m}\left({\mathit{y}}^{\mathrm{o}}\right)\in \left\{\mathrm{0.5},\mathrm{1},\mathrm{1.5}\right\}$, with all the other parameters being fixed to the reference. The results are displayed in Fig. 8. Figure 8a corresponds to the case m(y^o)=0.5. The resulting mass of the analysed observables is then $\mathrm{m}\left({\mathit{x}}^{\mathrm{a}}\right)=\mathrm{m}\left({\mathit{x}}^{\mathrm{b}}\right)=\mathrm{m}\left({\mathit{x}}^{\mathrm{o}}\right)=\mathrm{0.79}$. The adjustment of x^b compared with y^b and the adjustment of x^o compared with y^o, which are required to balance x^b and x^o, are patent. Figure 8b corresponds to the case m(y^o)=1. The resulting mass of the analysed observables is then $\mathrm{m}\left({\mathit{x}}^{\mathrm{a}}\right)=\mathrm{m}\left({\mathit{x}}^{\mathrm{b}}\right)=\mathrm{m}\left({\mathit{x}}^{\mathrm{o}}\right)=\mathrm{1}$. No adjustment is required here because m(y^o)=m(y^b), and x^o and y^o as well as x^b and y^b coincide. Finally, the mass of y^o is set to m(y^o)=1.5 in Fig. 8c. The resulting mass of the analysed observables is then $\mathrm{m}\left({\mathit{x}}^{\mathrm{a}}\right)=\mathrm{m}\left({\mathit{x}}^{\mathrm{b}}\right)=\mathrm{m}\left({\mathit{x}}^{\mathrm{o}}\right)=\mathrm{1.34}$. The adjustment of x^b compared with y^b and the adjustment of x^o compared with y^o, which are required to balance x^b and x^o, are visually obvious, but the balancing goes in the opposite direction compared with Fig. 8a, as expected.

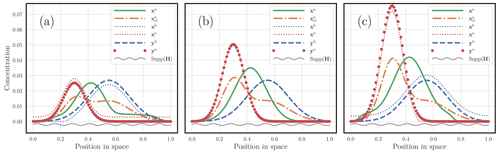
Figure 8 A hybrid OTDA 3D-Var analysis with one-dimensional physical states, where only the mass of y^o is varied. Its mass is m(y^o)=0.5 in panel (a), m(y^o)=1 in panel (b), and m(y^o)=1.5 in panel (c). The dashed blue curve corresponds to the first guess y^b; the red dots correspond to the observations y^o; the analysis state x^a is the solid green curve; and the analysed observables x^b and x^o are blue and red dotted curves, respectively. The support of the observation is underlined by a wavy grey segment. The corresponding classical analysis is also plotted with a dot-dash orange curve. The x axis corresponds to the position in space; the y axis corresponds to the concentration value of the fields.

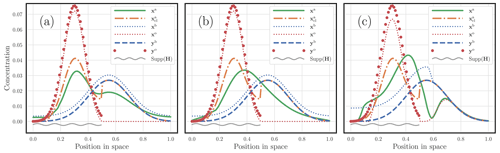
3.1.2 Varying the sparseness of the observation operator

In this second experiment, with all of the other parameters being fixed to their reference value, only a fraction of the domain is observed, over $\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{4}}\right]$, $\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right]$, and $\left[\mathrm{0},\frac{\mathrm{3}}{\mathrm{4}}\right]$, where $\mathbf{H}\in {\mathcal{O}}_{{\mathcal{N}}_{\mathrm{o}}\times N_{\mathrm{o}}}^{+}$ with ${\mathcal{N}}_{\mathrm{o}}=N_{\mathrm{o}}/\mathrm{4},N_{\mathrm{o}}/\mathrm{2},\mathrm{3}{N}_{\mathrm{o}}/\mathrm{4}$, and $H_l^j={\mathit{\delta }}_{l,j}$ for $l\in \left[\right[\mathrm{1},{\mathcal{N}}_{\mathrm{o}}\left]\right]$ and $j\in \left[\right[\mathrm{1},N_{\mathrm{o}}\left]\right]$.

The masses of the states that are built to generate y^b and y^o, before applying any observation operator, are set to 1 and 1.5, respectively. As a result, we have m(y^b)=1, but m(y^o) may depart from 1.5 depending on H. The fully observed case corresponds to Fig. 8c. The results are displayed in Fig. 9. It shows how smooth the OTDA solution can be compared with that of classical DA. However, as in Fig. 9a, OTDA can also handle obviously diverging sources of information, as is the case when the support of H is $\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{4}}\right]$ and when y^o and y^b can be seen to be barely consistent. In that case, the OTDA solution is smooth but bimodal.

Figure 9 A hybrid OTDA 3D-Var analysis with one-dimensional physical states, where the observation operator is increasingly sparse. The support of H is $\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{4}}\right]$ for panel (a), $\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right]$ for panel (b), and $\left[\mathrm{0},\frac{\mathrm{3}}{\mathrm{4}}\right]$ for panel (c). See Fig. 8 for a description of the legend.

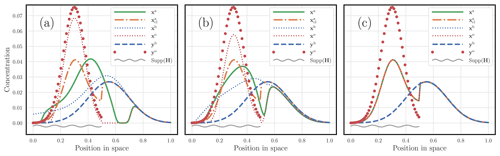
3.1.3 Changing the nature of the cost metric

In this third experiment, we choose the cost metric to be of the form $[{\mathbf{C}}_{\mathrm{ba}}{]}_{ik}=|r_i^{\mathrm{b}}-r_k^{\mathrm{a}}{|}^{\mathit{\alpha }}$ and $[{\mathbf{C}}_{\mathrm{oa}}{]}_{jk}=|r_j^{\mathrm{o}}-r_k^{\mathrm{a}}{|}^{\mathit{\alpha }}$. Only half of the domain is observed over $\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right]$, as in the case of Fig. 9b. As the mass of the state used to produce y^o is 1.5, we have a slightly different m(y^o)=1.49, with the rest of the mass being located in the unobserved part of the domain. All of the other parameters follow the reference set-up. The results are displayed in Fig. 10. For Fig. 10a, α is set to 0.5. For Fig. 10b, α is set to 1. For Fig. 10c, the cost metric is piecewise; it is quadratic, i.e. α=2, for pairs of sites separated by less than 10⁻¹, i.e. $|r_i^{\mathrm{b}}-r_k^{\mathrm{a}}|=|r_j^{\mathrm{o}}-r_k^{\mathrm{a}}|\le {\mathrm{10}}^{-\mathrm{1}}$, whereas the costs are chosen to be infinite for pairs of sites beyond this range. Hence, transport is prohibited beyond a distance of 10⁻¹. The case of a pure quadratic cost corresponds to Fig. 9b. The impact on the shape of the OTDA analysis is very significant and suggests that one could easily tailor their own cost to suit their specific DA problem.

Figure 10 A hybrid OTDA 3D-Var analysis with one-dimensional physical states, where the cost metrics are changed. See the bulk of the text for a definition of the three cost metrics. See Fig. 8 for a description of the legend.

3.1.4 Classical data assimilation as a sub-case of the hybrid optimal transport data assimilation

In the fourth experiment, we would like to numerically check the theoretical prediction of Sect. 2.4.3. Consider again the reference configuration; however, only half of the domain, over $\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right]$, is observed, $\mathbf{H}\in {\mathcal{O}}_{{\mathcal{N}}_{\mathrm{o}}\times N_{\mathrm{o}}}^{+}$ with ${\mathcal{N}}_{\mathrm{o}}=N_{\mathrm{o}}/\mathrm{2}$ and $H_l^j={\mathit{\delta }}_{l,j}$ for $l\in \left[\right[\mathrm{1},{\mathcal{N}}_{\mathrm{o}}\left]\right]$ and $j\in \left[\right[\mathrm{1},N_{\mathrm{o}}\left]\right]$. Most importantly, the cost metric has a quadratic dependence on the distance between sites, i.e. $[{\mathbf{C}}_{\mathrm{ba}}{]}_{ik}=\mathit{\lambda }|r_i^{\mathrm{b}}-r_k^{\mathrm{a}}{|}^{\mathrm{2}}$ and $[{\mathbf{C}}_{\mathrm{oa}}{]}_{jk}=\mathit{\lambda }|r_j^{\mathrm{o}}-r_k^{\mathrm{a}}{|}^{\mathrm{2}}$. The case λ=1 corresponds to Fig. 9b. Figure 11 shows the results corresponding to λ=10³ for panel (a), λ=10⁴ for panel (b), and λ=10⁶ for panel (c). When λ is increased, the OTDA analysis should tend to the classical DA solution. This is indeed corroborated by Fig. 11 and supports the claim of Sect. 2.4.3. Note that, as opposed to the three earlier experiments, we had to tune ε here, as the wide range of λ has a significant impact on the balance of the key terms of the cost function (transport cost, discrepancy errors, and regularisation).

Figure 11 Scaling up the cost metrics λC_ba and λC_oa with increasing λ, the OTDA analysis converges to the classical DA analysis. Panels (a), (b), and (c) correspond to the scaling values $\mathit{\lambda }={\mathrm{10}}^{\mathrm{3}},{\mathrm{10}}^{\mathrm{4}},$ and 10⁶, respectively. See Fig. 8 for a description of the legend.

3.2 Two-dimensional examples

Considering the case in which the physical space of the fields is two-dimensional, we perform a couple of 3D-Var analyses on concentration fields (puffs of a pollutant). The states are discretised in the domain [0,1]² at sites/grid cells ${\mathit{r}}_{i,j}^{\star }=\left((i-\frac{\mathrm{1}}{\mathrm{2}})/N_{\star }^x,(j-\frac{\mathrm{1}}{\mathrm{2}})/N_{\star }^y\right)$ for $(i,j)\in \left[\right[\mathrm{1},N_{\star }^x\left]\right]\times \left[\right[\mathrm{1},N_{\star }^y\left]\right]$, with $\star =\mathrm{b},\mathrm{o}$, and a. We choose $N_{\mathrm{b}}^x=N_{\mathrm{b}}^y=N_{\mathrm{o}}^x=N_{\mathrm{o}}^y=N_{\mathrm{a}}^x=N_{\mathrm{a}}^y={\mathrm{10}}^{\mathrm{2}}$, such that $N_{\mathrm{b}}=N_{\mathrm{o}}=N_{\mathrm{a}}={\mathrm{10}}^{\mathrm{4}}$. Hence, the number of control variables is 3×10⁴. The observation vectors are y^b and y^o. As y^b is a fully observed instance of x^b, we have 𝒩_b=N_b, while 𝒩_o may differ from N_o depending on the definition of the observation operator H. Moreover, we choose (Gaussian statistics)

$$\begin{array}{}\text{(40)}& {\mathit{\zeta }}_{\mathrm{b}}\left({\mathit{e}}_{\mathrm{b}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}}}{∥{\mathit{e}}_{\mathrm{b}}∥}^{\mathrm{2}},{\mathit{\zeta }}_{\mathrm{b}}\left({\mathit{e}}_{\mathrm{o}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\sigma }}_{\mathrm{o}}^{\mathrm{2}}}}{∥{\mathit{e}}_{\mathrm{o}}∥}^{\mathrm{2}}.\end{array}$$

Here, ${\mathit{\sigma }}_{\mathrm{b}}={\mathit{\sigma }}_{\mathrm{o}}={\mathrm{10}}^{-\mathrm{2}}$. The entropic regularisation parameter is set to $\mathit{\epsilon }={\mathrm{10}}^{-\mathrm{3}}$.

The first analysis is displayed in Fig. 12. The observation operator H is the identity, but its support is restricted to the subdomain [0,0.6]². The plumes of pollutants y^b and y^o are generated from states formed as combinations of bell-like puffs. The system is unbalanced with m(y^b)=1.35 and m(y^o)=0.73. The cost metric has a quadratic dependence on the distance between sites, i.e. $[{\mathbf{C}}_{\mathrm{ba}}{]}_{ik}={∥{\mathit{r}}_i^{\mathrm{b}}-{\mathit{r}}_k^{\mathrm{a}}∥}_{\mathrm{2}}^{\mathrm{2}}$ and $[{\mathbf{C}}_{\mathrm{oa}}{]}_{jk}={∥{\mathit{r}}_j^{\mathrm{o}}-{\mathit{r}}_k^{\mathrm{a}}∥}_{\mathrm{2}}^{\mathrm{2}}$. The OTDA analysis is clearly smoother than the classical solution. The classical solution does not cope very well with the seemingly disagreeing sources of information y^b and y^o, generating sharp transitions in the classical analysis. If y^b and y^o were consistently obtained from a truth perturbed with errors with short-range correlation, i.e. if they were drawn from the true prior distribution and in the absence of mislocation errors, then the classical analysis would be as good as it can be, whereas the OTDA solution may be too safe, i.e. too smooth. However, if one believes that structural errors and, in particular, location errors can impact y^b and y^o, then the classical solution is improper and the OTDA analysis preferable.

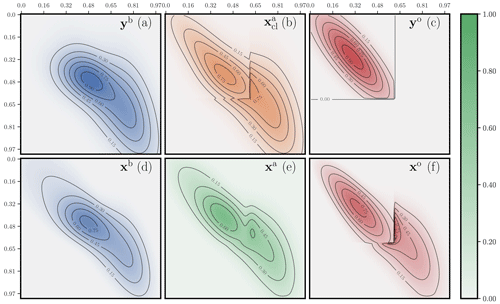
Figure 12 Two-dimensional concentration maps (plumes) of a hybrid OTDA analysis for the first configuration. The observations y^b and y^o; the analysed observables x^b and x^a, i.e. the state analysis; x^o; and the corresponding classical DA analysis ${\mathit{x}}_{\mathrm{cl}}^{\mathrm{a}}$ are displayed. All fields are rescaled so that their joint maximum is 1. All concentration maps use the same scale. The colour bar represents a unified contrast scale for the diverse field concentrations.

The second analysis is displayed in Fig. 13. The support of the observation operator H is again contained within the subdomain [0,0.6]², but only one of four grid cells is actually observed in this area. The observation states y^b and y^o are generated from the same states as for Fig. 12. The system is unbalanced with m(y^b)=1.35 and m(y^o)=0.18. The cost metric is defined to be the same as in Fig. 12. The OTDA analysis is even smoother in this case compared with the classical DA analysis. It is much less impacted by the sparseness of the observation operator. The classical solution has to account for the staggered observations in the top left corner of the domain because the first guess in that region is very uncertain. By contrast, the OTDA solution assumes that location errors are possible; hence, it moves around the mass corresponding to these observations so that the structure of the observation operator is not as impactful on the analysis.

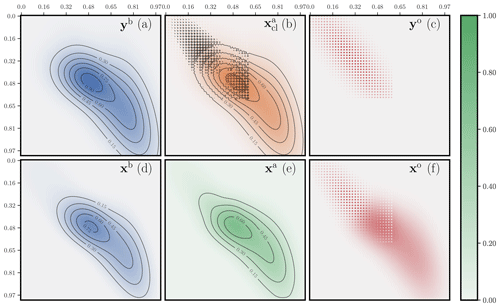
Figure 13 Two-dimensional concentrations maps of a hybrid OTDA analysis for the second configuration. The observations y^b and y^o; the analysed observables x^b and x^a, i.e. the state analysis; x^o; and the corresponding classical DA analysis are displayed. Compared to Fig. 12, only H has changed. The level sets in panels (c) and (f) are omitted because they are driven by the staggered observation operator.

4 Uncertainty quantification

In this section, we compute the posterior error covariance matrix P^a associated with the state analysis x^a, in order to complete the OTDA 3D-Var analysis description. There are many ways to proceed depending on the chosen regularisation and on the targeted degree of generality. Here, for the sake of consistency, we report on the way to derive P^a following the computation of the analysis state x^a proposed in Sect. 2.5.

4.1 Mathematical results

Let us denote the compounded vectors of the observations, of the Lagrange multipliers, and of the observables as well as the compounded observation operator by

$$\begin{array}{}\text{(41)}& \begin{array}{rl}& \mathit{y}\stackrel{\Delta }{=}\left[\begin{array}{c}{\mathit{y}}^{\mathrm{b}}\\ {\mathit{y}}^{\mathrm{o}}\end{array}\right],\mathit{f}\stackrel{\Delta }{=}\left[\begin{array}{c}{\mathit{f}}_{\mathrm{b}}\\ {\mathit{f}}_{\mathrm{o}}\end{array}\right],\\ & \mathit{x}\stackrel{\Delta }{=}\left[\begin{array}{c}{\mathit{x}}^{\mathrm{b}}\\ {\mathit{x}}^{\mathrm{o}}\end{array}\right],\mathcal{H}\stackrel{\Delta }{=}\left[\begin{array}{cc}{\mathbf{I}}_{\mathrm{b}}& \mathbf{0}\\ \mathbf{0}& \mathbf{H}\end{array}\right],\end{array}\end{array}$$

of size 𝒩_b+𝒩_o, 𝒩_b+𝒩_o, N_b+N_o, and $({\mathcal{N}}_{\mathrm{b}}+{\mathcal{N}}_{\mathrm{o}})\times (N_{\mathrm{b}}+N_{\mathrm{o}})$, respectively. Similarly, we define the sum of the error statistics by $\mathit{\zeta }\left(\mathit{f}\right)\stackrel{\Delta }{=}{\mathit{\zeta }}_{\mathrm{b}}\left({\mathit{f}}_{\mathrm{b}}\right)+{\mathit{\zeta }}_{\mathrm{o}}\left({\mathit{f}}_{\mathrm{o}}\right)$, whose Legendre–Fenchel transform is ${\mathit{\zeta }}^{\ast }\left(\mathit{f}\right)={\mathit{\zeta }}_{\mathrm{b}}^{\ast }\left({\mathit{f}}_{\mathrm{b}}\right)+{\mathit{\zeta }}_{\mathrm{o}}^{\ast }\left({\mathit{f}}_{\mathrm{o}}\right)$. Using this notation, we can recapitulate the key results of Sect. 2.5: the effective dual cost function is

$$\begin{array}{}\text{(42a)}& {\displaystyle }{J}_{\mathit{\epsilon }}^{\ast }\left(\mathit{f}\right)\stackrel{\Delta }{=}\mathit{\epsilon }{Z}_{\mathit{\epsilon }}\left(\mathit{f}\right)+{\mathit{\zeta }}^{\ast }\left(\mathit{f}\right)-{\mathit{f}}^{\top }\mathit{y},\text{(42b)}& {\displaystyle }{Z}_{\mathit{\epsilon }}\left(\mathit{f}\right)\stackrel{\Delta }{=}\mathrm{2}\sum _k\sqrt{Z_{\mathit{\epsilon },k}^{\mathrm{ba}}\left({\mathit{f}}_{\mathrm{b}}\right)Z_{\mathit{\epsilon },k}^{\mathrm{oa}}\left({\mathit{f}}_{\mathrm{o}}\right)}.\end{array}$$

Here, the analysis state reads

$$\begin{array}{}\text{(43)}& x_k^{\mathrm{a}}\left(\mathit{f}\right)=\sqrt{Z_{\mathit{\epsilon },k}^{\mathrm{ba}}\left({\mathit{f}}_{\mathrm{b}}\right)Z_{\mathit{\epsilon },k}^{\mathrm{oa}}\left({\mathit{f}}_{\mathrm{o}}\right)},\end{array}$$

where the dependence of the analysis state and the partition functions on f, f_b, and f_o is now emphasised and made explicit.

Any prior source of error in the system stems from the information vector y and hence drives the posterior error in the analysis x^a. That is why we are interested in the sensitivity of x^a with respect to y, i.e. $\mathit{\delta }{\mathit{x}}^{\mathrm{a}}={\partial }_{\mathit{y}}{\mathit{x}}^{\mathrm{a}}\mathit{\delta }\mathit{y}$. Denoting the expectation operator by 𝔼, the error covariance matrix is then defined by

$$\begin{array}{}\text{(44a)}& {\displaystyle }{\mathbf{P}}^{\mathrm{a}}=\mathbb{E}\left[\mathit{\delta }{\mathit{x}}^{\mathrm{a}}{\left(\mathit{\delta }{\mathit{x}}^{\mathrm{a}}\right)}^{\top }\right],\text{(44b)}& {\displaystyle }=\left({\partial }_{\mathit{y}}{\mathit{x}}^{\mathrm{a}}\right)\mathbb{E}\left[\mathit{\delta }\mathit{y}\mathit{\delta }{\mathit{y}}^{\top }\right]{\left({\partial }_{\mathit{y}}{\mathit{x}}^{\mathrm{a}}\right)}^{\top },\text{(44c)}& {\displaystyle }=\left({\partial }_{\mathit{y}}{\mathit{x}}^{\mathrm{a}}\right)\left({\partial }_{\mathit{f}}^{\mathrm{2}}{\mathit{\zeta }}^{\ast }\right){\left({\partial }_{\mathit{y}}{\mathit{x}}^{\mathrm{a}}\right)}^{\top },\end{array}$$

from which a matrix factor X^a of P^a, i.e. which satisfies ${\mathbf{P}}^{\mathrm{a}}={\mathbf{X}}^{\mathrm{a}}{\left({\mathbf{X}}^{\mathrm{a}}\right)}^{\top }$ and whose expressions are usually much shorter than those of P^a, can be extracted, up to the multiplication by an orthogonal matrix on the right:

$$\begin{array}{}\text{(45)}& {\mathbf{X}}^{\mathrm{a}}={\partial }_{\mathit{y}}{\mathit{x}}^{\mathrm{a}}({\partial }_{\mathit{f}}^{\mathrm{2}}{\mathit{\zeta }}^{\ast }{)}^{\frac{\mathrm{1}}{\mathrm{2}}}.\end{array}$$

To compute the sensitivity matrix ∂_yx^a, we leverage the stationarity of the dual cost function at the minimum:

$$\begin{array}{}\text{(46)}& {\partial }_{\mathit{f}}{J}_{\mathit{\epsilon }}^{\ast }\left(\mathit{f}\right(\mathit{y}),\mathit{y})=\mathbf{0}.\end{array}$$

We resort to the implicit function theorem:

$$\begin{array}{}\text{(47)}& \mathbf{0}={\mathrm{d}}_{\mathit{y}}{\partial }_{\mathit{f}}{J}_{\mathit{\epsilon }}^{\ast }\left(\mathit{f}\right(\mathit{y}),\mathit{y})={\partial }_{\mathit{f}}^{\mathrm{2}}{J}_{\mathit{\epsilon }}^{\ast }{\partial }_{\mathit{y}}\mathit{f}+{\partial }_{\mathit{f}}{\partial }_{\mathit{y}}{J}_{\mathit{\epsilon }}^{\ast },\end{array}$$

which yields

$$\begin{array}{}\text{(48)}& {\partial }_{\mathit{y}}\mathit{f}=-{\left[{\partial }_{\mathit{f}}^{\mathrm{2}}{J}_{\mathit{\epsilon }}^{\ast }\right]}^{-\mathrm{1}}{\partial }_{\mathit{f}}{\partial }_{\mathit{y}}{J}_{\mathit{\epsilon }}^{\ast }={\left[{\partial }_{\mathit{f}}^{\mathrm{2}}{J}_{\mathit{\epsilon }}^{\ast }\right]}^{-\mathrm{1}},\end{array}$$

as ${\partial }_{\mathit{f}}{\partial }_{\mathit{y}}{J}_{\mathit{\epsilon }}^{\ast }=-{\mathbf{I}}_{bo}$, where I_bo is the identity matrix in the compounded observation space ${\mathbb{R}}^{{\mathcal{N}}_{\mathrm{b}}+{\mathcal{N}}_{\mathrm{o}}}$. The sensitivity ∂_yx^a can now be computed using the Leibniz chain rule and Eq. (48):

$$\begin{array}{}\text{(49)}& {\displaystyle \frac{\partial {\mathit{x}}^{\mathrm{a}}}{\partial \mathit{y}}}={\displaystyle \frac{\partial {\mathit{x}}^{\mathrm{a}}}{\partial \mathit{f}}}{\displaystyle \frac{\partial \mathit{f}}{\partial \mathit{y}}}={\partial }_{\mathit{f}}{\mathit{x}}^{\mathrm{a}}{\left[{\partial }_{\mathit{f}}^{\mathrm{2}}{J}_{\mathit{\epsilon }}^{\ast }\right]}^{-\mathrm{1}}.\end{array}$$

Let us now compute the Jacobian and Hessian in the right-hand side of Eq. (49). To that end and in order to externalise the observation operator, we introduce ${\widehat{Z}}_{\mathit{\epsilon }}$ and ${\widehat{\mathit{x}}}_{\mathrm{a}}$, such that

$$\begin{array}{}\text{(50)}& {\widehat{Z}}_{\mathit{\epsilon }}(\mathit{\eta }={\mathcal{H}}^{\top }\mathit{f})\stackrel{\Delta }{=}{Z}_{\mathit{\epsilon }}\left(\mathit{f}\right),{\widehat{\mathit{x}}}_{\mathrm{a}}(\mathit{\eta }={\mathcal{H}}^{\top }\mathit{f})\stackrel{\Delta }{=}{\mathit{x}}^{\mathrm{a}}\left(\mathit{f}\right),\end{array}$$

and the related Jacobian and Hessians,

$$\begin{array}{}\text{(51a)}& {\displaystyle }{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{a}}\stackrel{\Delta }{=}{\partial }_{\mathit{\eta }}{\widehat{\mathit{x}}}_{\mathrm{a}},\text{(51b)}& {\displaystyle }{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}\stackrel{\Delta }{=}\mathit{\epsilon }{\partial }_{\mathit{\eta }}^{\mathrm{2}}{\widehat{Z}}_{\mathit{\epsilon }},\text{(51c)}& {\displaystyle }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}\stackrel{\Delta }{=}{\partial }_{\mathit{f}}^{\mathrm{2}}{\mathit{\zeta }}^{\ast }.\end{array}$$

${\widehat{Z}}_{\mathit{\epsilon }}$ and ${\widehat{\mathit{x}}}_{\mathrm{a}}$ can be shown to exist; they can be read off from the explicit expressions of Z_ε and x^a as functions of f. These Jacobian and Hessians depend on the choice of the regularisation operator and need to be computed analytically, which is simple but tedious; this is not reported here, as it is a regularisation-dependent calculation. The Hessian of the dual cost function Eq. (42a) can then be written as the sum

$$\begin{array}{}\text{(52)}& {\partial }_{\mathit{f}}^{\mathrm{2}}{J}_{\mathit{\epsilon }}^{\ast }={\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}+\mathcal{H}{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}{\mathcal{H}}^{\top },\end{array}$$

while the sensitivity matrix now reads

$$\begin{array}{}\text{(53)}& {\partial }_{\mathit{f}}{\mathit{x}}^{\mathrm{a}}={\mathbf{\Omega }}_{\mathrm{bo},\mathrm{a}}^{\top }{\mathcal{H}}^{\top }.\end{array}$$

Note that Ω_bo,bo can be interpreted as the covariance matrix of x, the compounded observable vector as defined in Eq. (41) (although seen as a random vector), under the assumption that x^b and x^o are connected via the W-barycentre x^a and the optimal transference plans P^ba and P^oa (all seen as random vectors). Combining Eqs. (52) and (53) with Eq. (45), we finally obtain the expression for a factor X^a of P^a:

$$\begin{array}{}\text{(54)}& {\mathbf{X}}^{\mathrm{a}}={\mathbf{\Omega }}_{\mathrm{bo},\mathrm{a}}^{\top }{\mathcal{H}}^{\top }{\left[{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}+\mathcal{H}{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}{\mathcal{H}}^{\top }\right]}^{-\mathrm{1}}{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{\frac{\mathrm{1}}{\mathrm{2}}}.\end{array}$$

Alternatively, we can use the Sherman–Morrison–Woodbury transformation, under the assumption that Ω_bo,bo is invertible:

$$\begin{array}{}\text{(55)}& {\mathbf{X}}^{\mathrm{a}}={\mathbf{\Omega }}_{\mathrm{bo},\mathrm{a}}^{\top }{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}^{-\mathrm{1}}{\left[{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}^{-\mathrm{1}}+{\mathcal{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\mathrm{1}}\mathcal{H}\right]}^{-\mathrm{1}}{\mathcal{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}.\end{array}$$

These formulas are similar to the normal equations of classical DA. However, it should be noted that, in Eqs. (54) and (55), all of the prior error statistics are encapsulated in Λ_bo,bo, whereas the impact of OT is encoded in Ω_bo,bo. To be concrete, note that, when using Gaussian statistics (Eq. 12), Λ_bo,bo would simply read

$$\begin{array}{}\text{(56)}& {\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}=\left[\begin{array}{cc}{\mathbf{\Lambda }}_{\mathrm{bb}}& \mathbf{0}\\ \mathbf{0}& {\mathbf{\Lambda }}_{\mathrm{oo}}\end{array}\right]=\left[\begin{array}{cc}\mathbf{B}& \mathbf{0}\\ \mathbf{0}& \mathbf{R}\end{array}\right].\end{array}$$

4.2 Interpretation

Further, we can perform a block decomposition of Ω onto the spaces of x^b and x^o:

$$\begin{array}{}\text{(57)}& {\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}\stackrel{\Delta }{=}\left[\begin{array}{cc}{\mathbf{\Omega }}_{\mathrm{bb}}& {\mathbf{\Omega }}_{\mathrm{bo}}\\ {\mathbf{\Omega }}_{\mathrm{bo}}^{\top }& {\mathbf{\Omega }}_{\mathrm{oo}}\end{array}\right].\end{array}$$

It can be shown that Ω_bo is proportional to the optimal transference plan of the effective transport between x^o and x^b and that the blocks of the diagonal are themselves diagonal and depend on the observable states:

$$\begin{array}{}\text{(58a)}& {\displaystyle }{\mathbf{\Omega }}_{\mathrm{bo}}={\displaystyle \frac{\mathrm{1}}{\mathit{\epsilon }}}{\mathbf{P}}^{\mathrm{bo}},\text{(58b)}& {\displaystyle }{\mathbf{\Omega }}_{\mathrm{bb}}={\displaystyle \frac{\mathrm{1}}{\mathit{\epsilon }}}\mathrm{diag}\left({\mathit{x}}^{\mathrm{b}}\right),\text{(58c)}& {\displaystyle }{\mathbf{\Omega }}_{\mathrm{oo}}={\displaystyle \frac{\mathrm{1}}{\mathit{\epsilon }}}\mathrm{diag}\left({\mathit{x}}^{\mathrm{o}}\right).\end{array}$$

For instance, this could be shown by the explicit computation of ${\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}=\mathit{\epsilon }{\partial }_{\mathit{\eta }}^{\mathrm{2}}{\widehat{Z}}_{\mathit{\epsilon }}$.

Let us now examine the impact of OT on the analysis error covariance matrix. We first define

$$\begin{array}{}\text{(59)}& \mathbf{\Delta }={\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}\mathcal{H}{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}^{\frac{\mathrm{1}}{\mathrm{2}}},\end{array}$$

whose thin singular value decomposition is UΣV^⊤, where U is an orthogonal matrix of size $({\mathcal{N}}_{\mathrm{b}}+{\mathcal{N}}_{\mathrm{o}})\times ({\mathcal{N}}_{\mathrm{b}}+{\mathcal{N}}_{\mathrm{o}})$, Σ is a rectangular and diagonal matrix of size $({\mathcal{N}}_{\mathrm{b}}+{\mathcal{N}}_{\mathrm{o}})\times (N_{\mathrm{b}}+N_{\mathrm{o}})$, and V is an orthogonal matrix of size $(N_{\mathrm{b}}+N_{\mathrm{o}})\times (N_{\mathrm{b}}+N_{\mathrm{o}})$. Then, we standardise Eq. (54) following, for example, Sect. 2.4.1 in Rodgers (2000):

$$\begin{array}{}\text{(60a)}& {\displaystyle }{\mathbf{X}}^{\mathrm{a}}={\mathbf{\Omega }}_{\mathrm{bo},\mathrm{a}}^{\top }{\mathcal{H}}^{\top }{\left[{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}+\mathcal{H}{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}{\mathcal{H}}^{\top }\right]}^{-\mathrm{1}}{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{\frac{\mathrm{1}}{\mathrm{2}}},\text{(60b)}& {\displaystyle }\begin{array}{rl}& ={\mathbf{\Omega }}_{\mathrm{bo},\mathrm{a}}^{\top }{\mathcal{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}\\ & \times {\left[{\mathbf{I}}_{bo}+{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}\mathcal{H}{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}{\mathcal{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}\right]}^{-\mathrm{1}},\end{array}\text{(60c)}& {\displaystyle }={\mathbf{\Omega }}_{\mathrm{bo},\mathrm{a}}^{\top }{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}{\mathbf{\Delta }}^{\top }{\left[{\mathbf{I}}_{bo}+\mathbf{\Delta }{\mathbf{\Delta }}^{\top }\right]}^{-\mathrm{1}},\text{(60d)}& {\displaystyle }={\mathbf{\Omega }}_{\mathrm{bo},\mathrm{a}}^{\top }{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}\mathbf{V}{\mathbf{\Sigma }}^{\top }{\left[{\mathbf{I}}_{bo}+\mathbf{\Sigma }{\mathbf{\Sigma }}^{\top }\right]}^{-\mathrm{1}}{\mathbf{U}}^{\top }.\end{array}$$

Defining $\mathit{\sigma }={\left(\mathbf{\Sigma }{\mathbf{\Sigma }}^{\top }\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}$, which is a square diagonal of size $({\mathcal{N}}_{\mathrm{b}}+{\mathcal{N}}_{\mathrm{o}})\times ({\mathcal{N}}_{\mathrm{b}}+{\mathcal{N}}_{\mathrm{o}})$, we obtain, up to a multiplication by an irrelevant orthogonal matrix on the right, an equivalent factor for P^a:

$$\begin{array}{}\text{(60e)}& {\mathbf{X}}^{\mathrm{a}}={\mathbf{\Omega }}_{\mathrm{bo},\mathrm{a}}^{\top }{\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}\mathbf{V}{\displaystyle \frac{\mathit{\sigma }}{{\mathbf{I}}_{bo}+{\mathit{\sigma }}^{\mathrm{2}}}}.\end{array}$$

The diagonal values of σ, denoted σ_i≥0, represent the independent degrees of freedom (dof) values of information that can be extracted from the observations, which, in our case, is the first guess y^b and the traditional observations y^o, in contrast to Rodgers (2000), who only considers the dof values from y^o. The higher the σ_i, the more information attached to the dof of index i and the more squeezed the corresponding direction in X^a and P^a. From Eq. (59) and, in particular, its transpose, ${\mathbf{\Delta }}^{\top }={\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}^{\frac{\mathrm{1}}{\mathrm{2}}}{\mathcal{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}$, we can trace the flow of any piece of information. Such information stems from the observation vectors; hence, its flow starts in Δ^⊤ from ${\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}$, the square root of the precision matrix ${\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\mathrm{1}}$. It is then transferred from the observation spaces to the observable spaces through 𝓗^⊤. It is finally optimally transported across the space of x^b and x^o by Ω_bo,bo, whose off-diagonal block is proportional to the transference plan P^bo. Hence, OT is not a primary source of uncertainty, as y^b and y^o can be, but moves information in between the observable spaces.

Let us now check the OTDA analysis error covariance matrix P^a in the classical DA limit. To that end, we study Eq. (54) in the classical limit. Similarly to Ω_bb and Ω_oo in Eq. (58a), Ω_aa is defined as the covariance matrix of x^a when only accounting for both OTs, and it can be shown that it reads

$$\begin{array}{}\text{(61)}& {\mathbf{\Omega }}_{\mathrm{aa}}={\displaystyle \frac{\mathrm{1}}{\mathit{\epsilon }}}\mathrm{diag}\left({\mathit{x}}^{\mathrm{a}}\right).\end{array}$$

When the cost tends to ${\mathbf{C}}_{\mathrm{bo}}^{\mathrm{\infty }}$, following the same arguments as in Sect. 2.4.3, x^b, x^o, and x^a must merge and, consequently, ${\mathbf{\Omega }}_{\mathrm{bo}}={\mathbf{\Omega }}_{\mathrm{aa}}={\mathbf{\Omega }}_{\mathrm{bb}}={\mathbf{\Omega }}_{\mathrm{oo}}$. Hence, in this limit, ${\mathbf{\Omega }}_{\mathrm{bo},\mathrm{bo}}={\mathbf{1}}_{\mathrm{2}}{\mathbf{\Omega }}_{\mathrm{aa}}{\mathbf{1}}_{\mathrm{2}}^{\top }$ and ${\mathbf{\Omega }}_{\mathrm{bo},\mathrm{a}}={\mathbf{1}}_{\mathrm{2}}{\mathbf{\Omega }}_{\mathrm{aa}}$, with ${\mathbf{1}}_{\mathrm{2}}=[\mathrm{1}\mathrm{1}{]}^{\top }$. Then, substituting these expressions of Ω_bo,bo and Ω_bo,a into Eq. (54), we get

$$\begin{array}{}\text{(62a)}& {\displaystyle }\begin{array}{rl}{\mathbf{X}}^{\mathrm{a}}& ={\mathbf{\Omega }}_{\mathrm{aa}}{\mathbf{1}}_{\mathrm{2}}^{\top }{\mathcal{H}}^{\top }{\left[{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}+\mathcal{H}{\mathbf{1}}_{\mathrm{2}}{\mathbf{\Omega }}_{\mathrm{aa}}{\mathbf{1}}_{\mathrm{2}}^{\top }{\mathcal{H}}^{\top }\right]}^{-\mathrm{1}}{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{\frac{\mathrm{1}}{\mathrm{2}}},\end{array}\text{(62b)}& {\displaystyle }\begin{array}{rl}& ={\mathbf{\Omega }}_{\mathrm{aa}}{\mathbf{1}}_{\mathrm{2}}^{\top }{\mathcal{H}}^{\top }{\left[{\mathbf{I}}_{bo}+{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\mathrm{1}}\mathcal{H}{\mathbf{1}}_{\mathrm{2}}{\mathbf{\Omega }}_{\mathrm{aa}}{\mathbf{1}}_{\mathrm{2}}^{\top }{\mathcal{H}}^{\top }\right]}^{-\mathrm{1}}{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}},\end{array}\text{(62c)}& {\displaystyle }\begin{array}{rl}& ={\mathbf{\Omega }}_{\mathrm{aa}}{\left[{\mathbf{I}}_{\mathrm{a}}+{\mathbf{1}}_{\mathrm{2}}^{\top }{\mathcal{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\mathrm{1}}\mathcal{H}{\mathbf{1}}_{\mathrm{2}}{\mathbf{\Omega }}_{\mathrm{aa}}\right]}^{-\mathrm{1}}{\mathbf{1}}_{\mathrm{2}}^{\top }{\mathcal{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}},\end{array}\text{(62d)}& {\displaystyle }\begin{array}{rl}& ={\left[{\mathbf{\Omega }}_{\mathrm{aa}}^{-\mathrm{1}}+{\mathbf{1}}_{\mathrm{2}}^{\top }{\mathcal{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\mathrm{1}}\mathcal{H}{\mathbf{1}}_{\mathrm{2}}\right]}^{-\mathrm{1}}{\mathbf{1}}_{\mathrm{2}}^{\top }{\mathcal{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\frac{\mathrm{1}}{\mathrm{2}}}.\end{array}\end{array}$$

Here, I_a is the identity matrix of size N_a. From Eq. (62b) to Eq. (62c), we relied on the shift matrix lemma (e.g. Asch et al., 2016). For ${\mathbf{\Omega }}_{\mathrm{aa}}^{-\mathrm{1}}$ in Eq. (62d) to exist, it must be assumed that ${\mathit{x}}^{\mathrm{a}}\in {\mathcal{O}}_{N_{\mathrm{a}}}^{+,\star }$; i.e. all the entries of x^a are positive. This is verified when using entropic regularisation with ε>0, no matter how small the entries of x^a are. Moreover, if x^a has zero entries, x^a can be represented as the limit of a sequence of positive discrete measures.

Now, as we have

$$\begin{array}{}\text{(63)}& {\mathbf{A}}^{-\mathrm{1}}\stackrel{\Delta }{=}{\mathbf{1}}_{\mathrm{2}}^{\top }{\mathcal{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{bo},\mathrm{bo}}^{-\mathrm{1}}\mathcal{H}{\mathbf{1}}_{\mathrm{2}}={\mathbf{\Lambda }}_{\mathrm{bb}}^{-\mathrm{1}}+{\mathbf{H}}^{\top }{\mathbf{\Lambda }}_{\mathrm{oo}}^{-\mathrm{1}}\mathbf{H},\end{array}$$

we conclude, from Eq. (62d), that the classical limit of the analysis error covariance matrix is

$$\begin{array}{}\text{(64a)}& {\displaystyle }{\mathbf{P}}^{\mathrm{a}}={\mathbf{X}}^{\mathrm{a}}{\left({\mathbf{X}}^{\mathrm{a}}\right)}^{\top }\text{(64b)}& {\displaystyle }={\left[{\mathbf{\Omega }}_{\mathrm{aa}}^{-\mathrm{1}}+{\mathbf{A}}^{-\mathrm{1}}\right]}^{-\mathrm{1}}{\mathbf{A}}^{-\mathrm{1}}{\left[{\mathbf{\Omega }}_{\mathrm{aa}}^{-\mathrm{1}}+{\mathbf{A}}^{-\mathrm{1}}\right]}^{-\mathrm{1}}.\end{array}$$

If the limit of x^a when $\mathit{\epsilon }\to {\mathrm{0}}^{+}$ is in ${\mathcal{O}}_{N_{\mathrm{a}}}^{+,\star }$, then ${\mathbf{\Omega }}_{\mathrm{aa}}^{-\mathrm{1}}=\mathit{\epsilon }\mathrm{diag}({\mathit{x}}^{\mathrm{a}}{)}^{-\mathrm{1}}$ must vanish. In this case,

$$\begin{array}{}\text{(65)}& {\mathbf{P}}^{\mathrm{a}}\underset{\mathit{\epsilon }\to {\mathrm{0}}^{+}}{⟶}\mathbf{A}={\left({\partial }_{{\mathit{f}}_{\mathrm{b}}}^{\mathrm{2}}{\mathit{\zeta }}_{\mathrm{b}}+{\mathbf{H}}^{\top }{\partial }_{{\mathit{f}}_{\mathrm{o}}}^{\mathrm{2}}{\mathit{\zeta }}_{\mathrm{o}}\mathbf{H}\right)}^{-\mathrm{1}},\end{array}$$

which, assuming Gaussian errors, would read ${\mathbf{P}}^{\mathrm{a}}={\left({\mathbf{B}}^{-\mathrm{1}}+{\mathbf{H}}^{\top }{\mathbf{R}}^{-\mathrm{1}}\mathbf{H}\right)}^{-\mathrm{1}}$, as expected from classical DA. However, if some of the entries of x^a vanish in the limit $\mathit{\epsilon }\to {\mathrm{0}}^{+}$, we suspect that the limit of P^a will be the classical analysis error covariance matrix A but with the columns and rows associated with the vanishing entries of x^a tapered to 0.

4.3 Numerical illustration

We consider the one-dimensional example where half of the domain is observed, over $\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right]$. Here, $\mathbf{H}\in {\mathcal{O}}_{{\mathcal{N}}_{\mathrm{o}}\times N_{\mathrm{o}}}^{+}$ with ${\mathcal{N}}_{\mathrm{o}}=N_{\mathrm{o}}/\mathrm{2}$ and $H_l^j={\mathit{\delta }}_{l,j}$ for $l\in \left[\right[\mathrm{1},{\mathcal{N}}_{\mathrm{o}}\left]\right]$ and $j\in \left[\right[\mathrm{1},N_{\mathrm{o}}\left]\right]$. Further, the observations are unbalanced, m(y^b)=1 and m(y^o)=1.49; they have been generated through 𝓗 by discrete measures of mass 1 and 1.5, respectively. Moreover, the cost metric has a quadratic dependence on the distance between sites, i.e. $[{\mathbf{C}}_{\mathrm{ba}}{]}_{ik}=\mathit{\lambda }|r_i^{\mathrm{b}}-r_k^{\mathrm{a}}{|}^{\mathrm{2}}$ and $[{\mathbf{C}}_{\mathrm{oa}}{]}_{jk}=\mathit{\lambda }|r_j^{\mathrm{o}}-r_k^{\mathrm{a}}{|}^{\mathrm{2}}$, where λ=10³. We use the results of Sect. 4.1 to compute the analysis error covariance matrix P^a, the transference plan P^bo, and the Jacobian Ω_bo,a. The numerical results are displayed in Fig. 14. The OTDA analysis state is bimodal, with some mass being left over to the right of the domain to account for the long tail of the first guess, which is far from the observation support. Hence, there is a vanishing field region, roughly [0.6,0.7], which separates the two components of the analysis state. As expected from OT theory, P^bo seems to converge towards a (non-trivial and barely differentiable) Monge map which, in this discrete context, has two branches, separated by the gap created by the vanishing field region. The analysis error covariance matrix P^a seems to converge to a diagonal matrix, with the exception of the vanishing field region. Indeed, there seems to be an uncertainty with respect to how much mass should be transferred from the first guess tail [0.7,1] to the main region [0,0.6]. This is given away by variance peaks near the edges of the gap and by negative covariances between the two edge points of the gap.

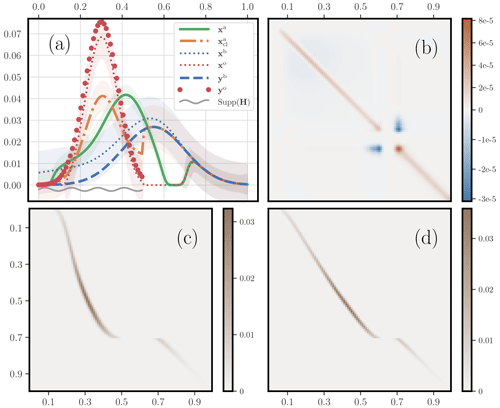
Figure 14 Illustration of the second-order analysis of an OTDA 3D-Var. Panel (a) shows the same plot as Fig. 11a but with the addition of shaded regions delineated by plus and minus the standard deviations about the estimates for ${\mathit{x}}^{\mathrm{a}},{\mathit{x}}_{\mathrm{cl}}^{\mathrm{a}},{\mathit{x}}^{\mathrm{b}}$, and x^o. These standard deviations are computed from the diagonal of the diagnosed posterior error covariance matrices associated with x^a, ${\mathit{x}}_{\mathrm{cl}}^{\mathrm{a}}$, x^b, and x^o. Panel (b) displays the analysis error covariance matrix P^a. Panel (c) shows the optimal transference plan P^bo. Panel (d) shows the a,b block part of the Jacobian matrix Ω_bo,a, which is denoted Ω_ba.

5 Conclusions

In this paper, we have introduced a theoretical framework for integrating nonlocal optimal transport (OT) metrics into data assimilation (DA), which we refer to as hybrid OTDA. This framework addresses the inconsistencies initially identified by Feyeux et al. (2016) when local metrics in classical DA are replaced with nonlocal ones based on OT.

Our focus has been on defining a 3D-Var approach for hybrid OTDA and deriving the first- and second-order moments of its analysis. The hybrid OTDA 3D-Var method blends classical DA and its background and observation error statistics with a Wasserstein barycentre problem involving the observables associated with the first guess and the observation vector. Importantly, our work demonstrates that classical DA is encompassed within this theoretical framework.

We have shown that this optimisation problem can be decomposed and simplified into a hybrid OTDA problem with a single OT problem based on an effective cost. This first problem yields the estimated x^b and x^o, followed by a pure W-barycentre problem involving these states, whose solution is known as the McCann interpolant. This W-barycentre computation serves as the final analysis step.

Our proposed method can be applied to sparsely and noisily observed systems, as expected from a robust DA method. It can also accommodate non-trivial error statistics typical of a 3D-Var approach. Furthermore, we have illustrated the method's flexibility in defining cost metrics through various one- and two-dimensional numerical examples. We have empirically checked how the OTDA analysis shifts towards the classical DA analysis, within the OTDA framework. Note that, for now, some limitations apply; mainly, the framework is presently meant for non-negative fields.

While we have looked into several other promising developments regarding our methodology, we have chosen not to report them in this paper. These developments will be the subject of a future publication and include the following:

• the derivation of a Bayesian and probabilistic standpoint on OTDA;

• a generalised formalism enforcing physical regularisation, such as smoothness of the field, on the analysis state;

• a stochastic matrix formalism, which is a substitute to using transference plans but could offer more robustness in the presence of entropic regularisation;

• employing cost matrices defined across several spaces, which is useful for realistic application where x^b and x^o lie in very distinct spaces, such as the space of emission of a pollutant and the space of the pollutant concentrations, respectively.

While our primary focus in this paper was on the derivation and understanding of key cost functions within the hybrid OTDA framework, we did not delve much into the numerical challenges, algorithmic complexity, or computing acceleration. For this aspect of the developments, we would rather rely on developments from OT experts, who are continuously improving the efficiency of numerical OT (e.g. Flamary et al., 2021).

In addition to strengthening the developments mentioned above, our future research will explore the application of the hybrid OTDA formalism in a sequential DA framework, as this paper concentrated solely on static analysis. We are also interested in investigating the role played by error statistics and cost metrics $\left\{{\mathit{\zeta }}_{\mathrm{b}},{\mathit{\zeta }}_{\mathrm{o}},{\mathbf{C}}_{\mathrm{ba}},{\mathbf{C}}_{\mathrm{oa}}\right\}$ and their balancing in the hybrid OTDA analysis as well as in developing their objective tuning.

Appendix A: From the primal to the dual cost function for the full problem

This appendix is dedicated to the derivation of the transformation from a Lagrangian variant of the primal problem to the dual cost function (Eq. 20). It takes the form of the following series of transformations of the problem (from a Lagrangian to a dual cost function):

$$\begin{array}{}\text{(A1a)}& {\displaystyle }\begin{array}{rl}\mathcal{L}=& \underset{{\mathit{x}}^{\mathrm{b}}{\mathit{x}}^{\mathrm{o}}{\mathit{x}}^{\mathrm{a}}}{min}[\underset{{\mathit{f}}_{\mathrm{b}}}{max}\left\{({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{b}}{)}^{\top }{\mathit{f}}_{\mathrm{b}}-{\mathit{\zeta }}_{\mathrm{b}}^{\ast }({\mathit{f}}_{\mathrm{b}})\right\}\\ & +\underset{{\mathit{f}}_{\mathrm{o}}}{max}\left\{({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{o}}{)}^{\top }{\mathit{f}}_{\mathrm{o}}-{\mathit{\zeta }}_{\mathrm{o}}^{\ast }({\mathit{f}}_{\mathrm{o}})\right\}\\ & +\underset{\mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o},\mathrm{a}}^{+}}{min}\mathit{\{}{P}_{ijk}{C}_{\mathrm{ba}}^{ik}+P_{ijk}{C}_{\mathrm{oa}}^{jk}\\ & +\underset{{\mathit{h}}_{\mathrm{b}}{\mathit{h}}_{\mathrm{o}}{\mathit{f}}_{\mathrm{a}}}{max}\mathit{\{}{h}_i^{\mathrm{b}}\left(x_i^{\mathrm{b}}-P_{ijk}{\mathrm{1}}_{\mathrm{o}}^j{\mathrm{1}}_{\mathrm{a}}^k\right)\\ & +h_j^{\mathrm{o}}\left(x_j^{\mathrm{o}}-P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{a}}^k\right)\\ & +f_{\mathrm{a}}^k\left(x_k^{\mathrm{a}}-P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j\right)\mathit{\left\}}\mathit{\right\}}],\end{array}\text{(A1b)}& {\displaystyle }\begin{array}{rl}=& \underset{{\mathit{x}}^{\mathrm{a}}{\mathit{x}}^{\mathrm{b}}{\mathit{x}}^{\mathrm{o}}}{min}\left[\underset{{\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}}}{max}\mathit{\right\{}({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{b}}{)}^{\top }{\mathit{f}}_{\mathrm{b}}\\ & -{\mathit{\zeta }}_{\mathrm{b}}^{\ast }\left({\mathit{f}}_{\mathrm{b}}\right)+({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{o}}{)}^{\top }{\mathit{f}}_{\mathrm{o}}\\ & -{\mathit{\zeta }}_{\mathrm{o}}^{\ast }\left({\mathit{f}}_{\mathrm{o}}\right)\mathit{\}}+\underset{{\mathit{h}}_{\mathrm{b}}{\mathit{h}}_{\mathrm{o}}{\mathit{f}}_{\mathrm{a}}}{max}\underset{\mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o},\mathrm{a}}^{+}}{min}\mathit{\{}{P}_{ijk}{C}_{\mathrm{ba}}^{ik}+P_{ijk}{C}_{\mathrm{oa}}^{jk}\\ & +h_i^{\mathrm{b}}\left(x_i^{\mathrm{b}}-P_{ijk}{\mathrm{1}}_{\mathrm{o}}^j{\mathrm{1}}_{\mathrm{a}}^k\right)+h_j^{\mathrm{o}}\left(x_j^{\mathrm{o}}-P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{a}}^k\right)\\ & +f_{\mathrm{a}}^k\left(x_k^{\mathrm{a}}-P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j\right)\mathit{\left\}}\right],\end{array}\text{(A1c)}& {\displaystyle }\begin{array}{rl}=& \underset{\begin{array}{c}{\mathit{h}}_{\mathrm{b}}{\mathit{h}}_{\mathrm{o}}{\mathit{f}}_{\mathrm{a}}\\ {\mathit{f}}_{\mathrm{b}}{\mathit{f}}_{\mathrm{o}}\end{array}}{max}\underset{\begin{array}{c}{\mathit{x}}^{\mathrm{a}}{\mathit{x}}^{\mathrm{b}}{\mathit{x}}^{\mathrm{o}}\\ \mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o},\mathrm{a}}^{+}\end{array}}{min}\\ & \left[\right({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{b}}{)}^{\top }{\mathit{f}}_{\mathrm{b}}-{\mathit{\zeta }}_{\mathrm{b}}^{\ast }\left({\mathit{f}}_{\mathrm{b}}\right)\\ & +({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{o}}{)}^{\top }{\mathit{f}}_{\mathrm{o}}-{\mathit{\zeta }}_{\mathrm{o}}^{\ast }({\mathit{f}}_{\mathrm{o}})+P_{ijk}{C}_{\mathrm{ba}}^{ik}+P_{ijk}{C}_{\mathrm{oa}}^{jk}\\ & +h_i^{\mathrm{b}}\left(x_i^{\mathrm{b}}-P_{ijk}{\mathrm{1}}_{\mathrm{o}}^j{\mathrm{1}}_{\mathrm{a}}^k\right)+h_j^{\mathrm{o}}\left(x_j^{\mathrm{o}}-P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{a}}^k\right)\\ & +f_{\mathrm{a}}^k\left(x_k^{\mathrm{a}}-P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j\right)],\end{array}\text{(A1d)}& {\displaystyle }\begin{array}{rl}=& \underset{{\mathit{f}}_{\mathrm{b}}{\mathit{f}}_{\mathrm{o}}}{max}\mathit{\{}{\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{y}}^{\mathrm{b}}+{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{y}}^{\mathrm{o}}-{\mathit{\zeta }}_{\mathrm{b}}^{\ast }({\mathit{f}}_{\mathrm{b}})-{\mathit{\zeta }}_{\mathrm{o}}^{\ast }({\mathit{f}}_{\mathrm{o}})\\ & +\underset{\begin{array}{c}{\mathit{h}}_{\mathrm{b}}{\mathit{h}}_{\mathrm{o}}{\mathit{f}}_{\mathrm{a}}\\ {\mathit{x}}^{\mathrm{a}}{\mathit{x}}^{\mathrm{b}}{\mathit{x}}^{\mathrm{o}}\mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o},\mathrm{a}}^{+}\end{array}}{min}\\ & \left[\right({\mathit{h}}_{\mathrm{b}}-{\mathit{f}}_{\mathrm{b}}{)}^{\top }{\mathit{x}}^{\mathrm{b}}+({\mathit{h}}_{\mathrm{o}}-{\mathbf{H}}^{\top }{\mathit{f}}_{\mathrm{o}}{)}^{\top }{\mathit{x}}^{\mathrm{o}}+{\mathit{f}}_{\mathrm{a}}^{\top }{\mathit{x}}^{\mathrm{a}}\\ & +P_{ijk}\left(C_{\mathrm{ba}}^{ik}+C_{\mathrm{oa}}^{jk}-h_i^{\mathrm{b}}{\mathrm{1}}_{\mathrm{o}}^j{\mathrm{1}}_{\mathrm{a}}^k-h_j^{\mathrm{o}}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{a}}^k-f_{\mathrm{a}}^k{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j\right)\left]\mathit{\right\}}\end{array},\end{array}$$

A1e$$\begin{array}{}\text{(A1e)}& {\displaystyle }\begin{array}{rl}=& \underset{{\mathit{f}}_{\mathrm{b}}{\mathit{f}}_{\mathrm{o}}}{max}[{\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{y}}^{\mathrm{b}}+{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{y}}^{\mathrm{o}}-{\mathit{\zeta }}_{\mathrm{b}}^{\ast }({\mathit{f}}_{\mathrm{b}})-{\mathit{\zeta }}_{\mathrm{o}}^{\ast }({\mathit{f}}_{\mathrm{o}})\\ & +\underset{\begin{array}{c}\mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o},\mathrm{a}}^{+}\end{array}}{min}{P}_{ijk}\left(C_{\mathrm{ba}}^{ik}+C_{\mathrm{oa}}^{jk}-f_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j{\mathrm{1}}_{\mathrm{a}}^k-H_l^j{f}_{\mathrm{o}}^l{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{a}}^k\right)].\end{array}\end{array}$$

In Eq. (A1a), the maps ${\mathit{\zeta }}_{\mathrm{b}}^{\ast }$ and ${\mathit{\zeta }}_{\mathrm{o}}^{\ast }$ are the Legendre–Fenchel transforms of the maps ζ_b and ζ_o, respectively. From Eq. (A1d) to Eq. (A1eA1e), taking the minimum over the observables x^b, x^o, and x^a implies enforcing h_b=f_b, ${\mathit{h}}_{\mathrm{o}}={\mathbf{H}}^{\top }{\mathit{f}}_{\mathrm{o}}$, and f_a=0. Hence, we obtain the dual problem which only depends on the Lagrange multipliers:

$$\begin{array}{}\text{(A2a)}& \begin{array}{rl}{\mathcal{L}}^{\ast }=\underset{({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}})\in {\mathcal{U}}_{\mathrm{bo}}^{\ast }({\mathbf{C}}_{\mathrm{ba}},{\mathbf{C}}_{\mathrm{oa}},\mathbf{H})}{max}\mathit{\{}& {\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{y}}^{\mathrm{b}}+{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{y}}^{\mathrm{o}}\\ & -{\mathit{\zeta }}_{\mathrm{b}}^{\ast }\left({\mathit{f}}_{\mathrm{b}}\right)-{\mathit{\zeta }}_{\mathrm{o}}^{\ast }\left({\mathit{f}}_{\mathrm{o}}\right)\mathit{\}},\end{array}\end{array}$$

where the ∗ symbol refers to dual and where the polyhedron ${\mathcal{U}}_{\mathrm{bo}}^{\ast }({\mathbf{C}}_{\mathrm{ba}},{\mathbf{C}}_{\mathrm{oa}},\mathbf{H})$ is defined by

$$\begin{array}{}\text{(A2b)}& \begin{array}{rl}{\mathcal{U}}_{\mathrm{bo}}^{\ast }({\mathbf{C}}_{\mathrm{ba}},{\mathbf{C}}_{\mathrm{oa}},& \mathbf{H}\left)\stackrel{\Delta }{=}\mathit{\right\{}{\mathit{f}}_{\mathrm{b}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{b}}},{\mathit{f}}_{\mathrm{o}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{o}}}:\\ & \forall i,j,k,f_{\mathrm{b}}^i+f_{\mathrm{o}}^l{H}_l^j\le C_{\mathrm{ba}}^{ik}+C_{\mathrm{oa}}^{jk}\mathit{\}}.\end{array}\end{array}$$

The inequality constraints of the polyhedron ${\mathcal{U}}_{\mathrm{bo}}^{\ast }$ stem from the positivity constraint P_ijk≥0 in Eq. (A1eA1e). Very importantly, we have the coincidence of the minimum of the primal problem with the maximum of the dual problem $\mathcal{L}={\mathcal{L}}^{\ast }$, a property called strong duality (see Sect. 5.2 in Boyd and Vandenberghe, 2004). Strong duality can, for instance, be achieved if both the primal and dual cost functions are convex, which is the case here.

Appendix B: Derivation of the two-step hybrid optimal transport data assimilation algorithm

Here, we derive the two-step algorithm elaborated in Sect. 2.4.2. Moreover, entropic regularisation is added to the problem.

B1 First step: simplified hybrid optimal transport data assimilation problem

The first step of the full OTDA algorithm is a simplified OTDA problem based on a single OT problem driven by the cost C_bo. The corresponding high-level primal cost function is

$$\begin{array}{}\text{(B1)}& \begin{array}{rl}\mathcal{L}=\underset{{\mathit{x}}^{\mathrm{b}}\in {\mathcal{O}}_{\mathrm{b}}^{+}{\mathit{x}}^{\mathrm{o}}\in {\mathcal{O}}_{\mathrm{o}}^{+}}{min}\mathit{\{}& {\mathit{\zeta }}_{\mathrm{b}}({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{b}})+{\mathit{\zeta }}_{\mathrm{o}}({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{o}})\\ & +W_{{\mathbf{C}}_{\mathrm{bo}}}({\mathit{x}}^{\mathrm{b}},{\mathit{x}}^{\mathrm{o}})\mathit{\}}.\end{array}\end{array}$$

The associated (lower-level) primal cost function, adding entropic regularisation (ε>0), is then

$$\begin{array}{}\text{(B2a)}& \begin{array}{rl}{\mathcal{L}}_{\mathit{\epsilon }}=\underset{{\mathit{x}}^{\mathrm{b}}\in {\mathcal{O}}_{\mathrm{b}}^{+}{\mathit{x}}^{\mathrm{o}}\in {\mathcal{O}}_{\mathrm{o}}^{+}}{min}& \left[{\mathit{\zeta }}_{\mathrm{b}}\right({\mathit{y}}^{\mathrm{b}}-{\mathit{x}}^{\mathrm{b}})+{\mathit{\zeta }}_{\mathrm{o}}({\mathit{y}}^{\mathrm{o}}-\mathbf{H}{\mathit{x}}^{\mathrm{o}})\\ & +\underset{\mathbf{P}\in {\mathcal{U}}_{\mathrm{bo}}}{min}\left(\mathit{\epsilon }\mathcal{K}\left(\mathbf{P}\right|\mathit{\nu })+P_{ij}{C}_{\mathrm{bo}}^{ij}\right)].\end{array}\end{array}$$

In this optimisation problem, the admissible set of transference plans, i.e. the set of all 2-tensors of non-negative entries whose marginals are x^b and x^o, is defined by

$$\begin{array}{}\text{(B2b)}& {\mathcal{U}}_{\mathrm{bo}}\stackrel{\Delta }{=}\left\{\mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o}}^{+}:\mathbf{P}{\mathbf{1}}_{\mathrm{o}}={\mathit{x}}^{\mathrm{b}},{\mathbf{P}}^{\top }{\mathbf{1}}_{\mathrm{b}}={\mathit{x}}^{\mathrm{o}}\right\}.\end{array}$$

As x^b and x^o are not predetermined, the prior transference plan ν cannot be selected from 𝒰_bo a priori. Hence, the simplest choice, which we decided to implement, is to set ν_ij to a constant, which assumes some statistical prior independence of x^b and x^o. A derivation of the dual problem equivalent to ℒ_ε can be obtained in the exact same way as in the previous subsection, although it is now less cluttered because there is only one OT to account for, instead of two. The associated Lagrangian is

$$\begin{array}{}\text{(B3)}& \begin{array}{rl}{\mathcal{L}}_{\mathit{\epsilon }}=& \underset{{\mathit{f}}_{\mathrm{b}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{b}}}{\mathit{f}}_{\mathrm{o}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{o}}}}{max}[{\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{y}}^{\mathrm{b}}+{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{y}}^{\mathrm{o}}-{\mathit{\zeta }}_{\mathrm{b}}^{\ast }({\mathit{f}}_{\mathrm{b}})-{\mathit{\zeta }}_{\mathrm{o}}^{\ast }({\mathit{f}}_{\mathrm{o}})\\ & +\underset{\mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o}}^{+}}{min}(\mathit{\epsilon }\sum _{ij}\left\{P_{ij}\ln {\displaystyle \frac{P_{ij}}{{\mathit{\nu }}_{ij}}}-P_{ij}+{\mathit{\nu }}_{ij}\right\}\\ & +P_{ij}\left\{C_{\mathrm{bo}}^{ij}-f_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j-H_l^j{f}_{\mathrm{o}}^l{\mathrm{1}}_{\mathrm{b}}^i\right\}\left)\right].\end{array}\end{array}$$

Again, the maps ${\mathit{\zeta }}_{\mathrm{b}}^{\ast }$ and ${\mathit{\zeta }}_{\mathrm{o}}^{\ast }$ are the Legendre–Fenchel transforms of the maps ζ_b and ζ_o, respectively. The variables f_b and f_o are Lagrange vectors; they are used to enforce the marginals of the transference plan associated with $W_{{\mathbf{C}}_{\mathrm{bo}}}$. The unconstrained minimisation over P, i.e. the inner minimisation problem in Eq. (B3), is obtained by cancelling the gradient with respect to P, which yields

$$\begin{array}{}\text{(B4)}& P_{ij}={\mathit{\nu }}_{ij}{e}^{\left(f_{\mathrm{b}}^i+f_{\mathrm{o}}^l{H}_l^j-C_{\mathrm{bo}}^{ij}\right)/\mathit{\epsilon }}.\end{array}$$

Substituting this solution into minus the Lagrangian −ℒ_ε gives the regularised dual problem

$$\begin{array}{}\text{(B5a)}& {\mathcal{J}}_{\mathit{\epsilon }}^{\ast }=\underset{{\mathit{f}}_{\mathrm{b}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{b}}}{\mathit{f}}_{\mathrm{o}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{o}}}}{min}{J}_{\mathit{\epsilon }}^{\ast }({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}}),\end{array}$$

with the associated Lagrangian

$$\begin{array}{}\text{(B5b)}& \begin{array}{rl}{J}_{\mathit{\epsilon }}^{\ast }({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}})=& \mathit{\epsilon }\left(Z_{\mathit{\epsilon }}-\mathrm{m}\left(\mathit{\nu }\right)\right)+{\mathit{\zeta }}_{\mathrm{b}}^{\ast }\left({\mathit{f}}_{\mathrm{b}}\right)+{\mathit{\zeta }}_{\mathrm{o}}^{\ast }\left({\mathit{f}}_{\mathrm{o}}\right)\\ & -{\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{y}}^{\mathrm{b}}-{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{y}}^{\mathrm{o}},\end{array}\end{array}$$

which relies on the partition function

$$\begin{array}{}\text{(B5c)}& Z_{\mathit{\epsilon }}=\sum _{ij}{P}_{ij}.\end{array}$$

The notation ${\mathcal{J}}_{\mathit{\epsilon }}^{\ast }$ and $J_{\mathit{\epsilon }}^{\ast }$, rather than ${\mathcal{L}}_{\mathit{\epsilon }}^{\ast }$ and $L_{\mathit{\epsilon }}^{\ast }$, signifies that we work on the opposite of ${\mathcal{L}}_{\mathit{\epsilon }}^{\ast }$ and $L_{\mathit{\epsilon }}^{\ast }$ so as to obtain a dual problem to be minimised rather than maximised. Most importantly, we have, under conditions that will be satisfied in the following, the coincidence of the two minima ${\mathcal{J}}_{\mathit{\epsilon }}^{\ast }=-{\mathcal{L}}_{\mathit{\epsilon }}$, i.e. strong duality. Assuming one can obtain a proper correspondence between the optimal f_b and f_o of the dual problem and x^b and x^o of the primal problem, this implies, once again, that the primal problem can be traded for the dual problem.

Even though the regularised optimisation problem is slightly different from the unregularised one, a difference which is controlled by the value of ε, the new dual optimisation problem is free, i.e. without constraints. It can be solved as it is, using, for instance, the L-BFGS-B minimiser (Liu and Nocedal, 1989). The advantage of the regularised dual formulation is twofold: (1) the dual cost function is unconstrained (free optimisation), and (2) we will trade a minimisation over N_b×N_o variables for a minimisation over N_b+N_o variables. This dual formulation can be viewed as a generalised physical-space statistical analysis system (PSAS) formalism (Courtier, 1997), an approach in which classical DA algebra is mostly carried out in observation space.

Once the optimal values for f_b and f_o are obtained, the optimal discrete Kantorovich transference plan P can be computed using Eq. (B4). As a result, as marginals of this transference plan, the solutions for the observables are

$$\begin{array}{}\text{(B6)}& x_i^{\mathrm{b}}=P_{ij}{\mathrm{1}}_{\mathrm{o}}^j=\sum _j{P}_{ij},x_j^{\mathrm{o}}=P_{ij}{\mathrm{1}}_{\mathrm{b}}^i=\sum _i{P}_{ij}.\end{array}$$

B2 Second step: Wasserstein barycentre

Now that we have obtained the observables x^b and x^o via Eq. (B6), we would like to compute their W-barycentre. The joint mass m of these observables can be computed as follows:

$$\begin{array}{}\text{(B7)}& m=\mathrm{m}\left({\mathit{x}}^{\mathrm{b}}\right)=\mathrm{m}\left({\mathit{x}}^{\mathrm{o}}\right).\end{array}$$

The high-level primal cost function of this W-barycentre problem is

$$\begin{array}{}\text{(B8)}& J_{\mathrm{w}}=\underset{{\mathit{x}}^{\mathrm{a}}\in {\mathcal{O}}_{N_{\mathrm{a}}}^{+}}{min}\left\{W_{{\mathbf{C}}_{\mathrm{ba}}}({\mathit{x}}^{\mathrm{b}},{\mathit{x}}^{\mathrm{a}})+W_{{\mathbf{C}}_{\mathrm{oa}}}({\mathit{x}}^{\mathrm{o}},{\mathit{x}}^{\mathrm{a}})\right\}.\end{array}$$

We have found and practised several ways to solve this problem. One way is to compute the McCann interpolant. This is theoretically elegant, but Eq. (26) did not leverage regularisation of the W-barycentre problem. Instead, the approach reported here is to use the dual optimisation problem, in conjunction with entropic regularisation at finite ε>0. We leverage our knowledge of the mass m resulting from the first step of the algorithm by enforcing the mass in the cost function, m(P)=m. This seems redundant, but it actually yields, by construction and very naturally, a numerically efficient algorithm comparable to the ad hoc log-domain scheme proposed in Sect. 4.4 of Peyré and Cuturi (2019).

Again, one way (although not the only way) to write the primal problem is to use a gluing transference plan, a 3-tensor whose marginals are x^b, x^o, and x^a:

$$\begin{array}{}\text{(B9a)}& \begin{array}{rl}{L}_{\mathit{\epsilon }}=\underset{{\mathit{x}}^{\mathrm{a}}\in {\mathcal{O}}_{N_{\mathrm{a}}}^{+}\mathbf{P}\in {\mathcal{U}}_{\mathrm{boa}}\left({\mathit{x}}^{\mathrm{a}}\right)}{min}\mathit{\{}& \mathbf{P}\cdot {\mathbf{C}}_{\mathrm{boa}}+\mathit{\epsilon }\mathcal{K}\left(\mathbf{P}\right|\mathit{\nu })\\ & +{\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{x}}^{\mathrm{b}}+{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{x}}^{\mathrm{o}}\mathit{\}},\end{array}\end{array}$$

where $[{\mathbf{C}}_{\mathrm{boa}}{]}_{ijk}=C_{\mathrm{ba}}^{ik}+C_{\mathrm{oa}}^{jk}$, the binary operator ⋅ denotes the contraction of tensors, and

$$\begin{array}{}\text{(B9b)}& \begin{array}{rl}{\mathcal{U}}_{\mathrm{boa}}(& {\mathit{x}}^{\mathrm{a}}\left)\stackrel{\Delta }{=}\mathit{\right\{}\mathbf{P}\in {\mathcal{O}}_{\mathrm{b},\mathrm{o},\mathrm{a}}^{+}:\forall i,P_{ijk}{\mathrm{1}}_{\mathrm{o}}^j{\mathrm{1}}_{\mathrm{a}}^k=x_i^{\mathrm{b}},\\ & \forall j,P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{a}}^k=x_j^{\mathrm{o}},\forall k,P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j=x_k^{\mathrm{a}}\mathit{\}}.\end{array}\end{array}$$

The 3-tensor ν is chosen to be ${\mathit{\nu }}_{ijk}=x_i^{\mathrm{b}}{x}_j^{\mathrm{o}}/\left(m{N}_{\mathrm{a}}\right)$, which is uniform in k and for which m(ν)=m. The resulting dual problem is

$$\begin{array}{}\text{(B10a)}& {\mathcal{J}}^{\ast }=\underset{{\mathit{f}}_{\mathrm{b}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{b}}}{\mathit{f}}_{\mathrm{o}}\in {\mathbb{R}}^{{\mathcal{N}}_{\mathrm{o}}}}{min}{J}^{\ast }({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}}),\end{array}$$

where the associated Lagrangian is

$$\begin{array}{ll}{\displaystyle }{J}^{\ast }({\mathit{f}}_{\mathrm{b}},{\mathit{f}}_{\mathrm{o}})=& {\displaystyle }\mathit{\epsilon }\left(m\ln {\displaystyle \frac{Z_{\mathit{\epsilon }}}{m}}+m-\mathrm{m}\left(\mathit{\nu }\right)\right)\\ \text{(B10b)}& {\displaystyle }& {\displaystyle }-{\mathit{f}}_{\mathrm{b}}^{\top }{\mathit{x}}^{\mathrm{b}}-{\mathit{f}}_{\mathrm{o}}^{\top }{\mathit{x}}^{\mathrm{o}},\end{array}$$

with the partition function

$$\begin{array}{}\text{(B10c)}& Z_{\mathit{\epsilon }}=\sum _{ijk}{\mathit{\nu }}_{ijk}{e}^{\left(f_{\mathrm{b}}^i+f_{\mathrm{o}}^l{H}_l^j-C_{\mathrm{ba}}^{ik}-C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }}.\end{array}$$

This partition function is elegant but impractical because, with high dimensionality, a 3-tensor might be too large to store and compute with. However the partition function in Eq. (B10c) can be simplified by noticing that

$$\begin{array}{}\text{(B11)}& Z_{\mathit{\epsilon }}=\sum _{ij}{\mathit{\nu }}_{ij}{e}^{\left(f_{\mathrm{b}}^i+f_{\mathrm{o}}^l{H}_l^j-C_{\mathrm{bo}}^{ij}\right)/\mathit{\epsilon }},\end{array}$$

where we introduced the effective cost metric

$$\begin{array}{}\text{(B12)}& {\left[{\mathbf{C}}_{\mathrm{bo}}\right]}_{ij}=-\mathit{\epsilon }\ln \left(\sum _k{\displaystyle \frac{{\mathit{\nu }}_{ijk}}{{\mathit{\nu }}_{ij}}}{e}^{-\left(C_{\mathrm{ba}}^{ik}+C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }}\right),\end{array}$$

which is the regularised cost – known in statistics and machine learning as a soft-plus transform – of Eq. (22c). The 2-tensor ν_ij plays the same role as that of the first step of the algorithm; we choose it as ${\mathit{\nu }}_{ij}=x_i^{\mathrm{b}}{x}_j^{\mathrm{o}}/m$, for which m(ν)=m. The dual problem now only involves 2-tensors and becomes numerically more efficient. Given the optimal f_b and f_o, the (glued) optimal transference plan P^boa is formally given by

$$\begin{array}{}\text{(B13)}& P_{ijk}^{\mathrm{boa}}={\displaystyle \frac{{\mathit{\nu }}_{ijk}}{Z_{\mathit{\epsilon }}}}{e}^{\left(f_{\mathrm{b}}^i+f_{\mathrm{o}}^l{H}_l^j-C_{\mathrm{ba}}^{ik}-C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }}.\end{array}$$

The W-barycentre x^a is then given as a marginal of P^boa:

$$\begin{array}{}\text{(B14a)}& {\displaystyle }{x}_k^{\mathrm{a}}& {\displaystyle }=P_{ijk}{\mathrm{1}}_{\mathrm{b}}^i{\mathrm{1}}_{\mathrm{o}}^j\text{(B14b)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{Z_{\mathit{\epsilon }}}}\sum _{ij}{\mathit{\nu }}_{ijk}{e}^{\left(f_{\mathrm{b}}^i+f_{\mathrm{o}}^l{H}_l^j-C_{\mathrm{ba}}^{ik}-C_{\mathrm{oa}}^{jk}\right)/\mathit{\epsilon }}.\end{array}$$

Because of the normalisation of the transference plan to m, the entropic regularisation exhibits a εmln Z_ε instead of εZ_ε. This systematically enforces normalisation in the computations of the gradients, as well as in the course of the numerical optimisation of the dual cost function, de facto working in the log domain. We experienced more stable computations and the ability to reach smaller ε, compared with the case without normalisation. This completes the solution through the two-step OTDA algorithm.