Clustering of settling microswimmers in turbulence

Clustering of plankton plays a vital role in several biological activities, including feeding, predation, and mating. Gyrotaxis is one of the mechanisms that induces clustering. A recent study (Candelier et al., 2022) reported a fluid inertial torque acting on a spherical microswimmer, which has the same effect as a gyrotactic torque. In this study, we model plankton cells as microswimmers that are subject to gravitational sedimentation as well as a fluid inertial torque. We use direct numerical simulations to obtain the trajectories of swimmers in homogeneous isotropic turbulence. We also investigate swimmers' clustering using Voronoï analysis. Our findings indicate that fluid inertial torque leads to notable clustering, with its intensity depending on the swimming and settling speeds of swimmers. Using Voronoï analysis, we demonstrate that swimmers preferentially sample downwelling regions where clustering is more prevalent.

1 Introduction

Plankton are known to form small-scale clusters in a turbulent environment (Rothschild and Osborn, 1988). These clusters can be down to the centimeter scale and significantly impact the basic life processes of plankton, such as feeding, predation, and mating. Gyrotaxis is one of the mechanisms that causes plankton to form clusters. Many plankton species experience a gravitational stabilizing torque that causes them to swim against gravity (Kessler, 1986). When plankton encounter flow shear, the gyrotactic torque opposes the fluid viscous torque and tends to stabilize the swimming direction of the plankton (Qiu et al., 2022b).

Gyrotactic plankton can form different kinds of clusters depending on the flow characteristics. For instance, plankton accumulate in the center or the wall regions in downward or upward pipe flow, respectively (Kessler, 1985). Plankton that are vertically migrating also form clusters when they encounter a shear layer that interrupts the migration (Durham et al., 2009). Plankton in turbulence form small-scale clusters that can be characterized by the swimming speed and the intensity of the gyrotactic torque. Durham et al. (2013) modeled plankton as spherical gyrotactic microswimmers and numerically studied their fractal clustering in homogeneous isotropic turbulence. They demonstrated that the intensity of clustering depends on the swimming speed and the intensity of gyrotaxis. Clustering is also shown to be correlated to the preferential sampling of downwelling regions (Durham et al., 2013). Later, Zhan et al. (2014) numerically investigated the effect of plankton shape on clustering. Elongated swimmers are more sensitive to fluid shear than spherical ones, weakening the clustering of strongly gyrotactic swimmers. However, elongation causes preferential alignment in local fluid structures, strengthening the clustering of weakly gyrotactic swimmers. To further clarify the complex relationship between clustering and the swimming speed, gyrotaxis, and shape of the swimmers, Gustavsson et al. (2016) and Fouxon and Leshansky (2015) established theories to describe clustering using stochastic models. These theories were later verified by direct numerical simulations of swimmers in homogeneous isotropic turbulence (Borgnino et al., 2018).

Previous studies have suggested that gyrotaxis originates from asymmetric body structures, such as nonuniform mass distribution (bottom-heaviness) (Kessler, 1985, 1986; Pedley and Kessler, 1987). However, a recent study by Candelier et al. (2022) modeled planktonic microorganisms as settling spherical squirmers and found that a fluid inertial torque drives the squirmer to swim against gravity. The squirmer model was proposed by Lighthill (1952) and improved by Blake (1971) to describe the slip velocity on the surface of microorganisms generated by the movement of cilia. The squirmer model can describe the typical propulsion modes, such as the puller mode for algae and the pusher mode for Escherichia coli, by changing model parameters. Both theory and simulations have indicated that fluid inertial torque on a settling squirmer is analogous to a gyrotactic torque, with a magnitude that is proportional to the settling and swimming speeds (Candelier et al., 2022). Planktonic organisms are usually slightly negatively buoyant and, thus, subject to a gravitational settling effect. For instance, dinoflagellates have a typical swimming speed of 300 µm s⁻¹ and a settling speed of 30 µm s⁻¹ (Smayda, 2010). Larger organisms, such as copepod nauplii, have swimming speeds of up to 1000 µm s⁻¹ and settling speeds of 200 µm s⁻¹ (Titelman and Kiørboe, 2003). As pointed out by Candelier et al. (2022), an organism with high swimming and settling speeds obtains a fluid inertial torque that is comparable to typical gyrotactic torque. However, earlier studies usually neglected the gravity sedimentation and the fluid inertial torque, highlighting the need to consider their effects on the motion of swimming and settling plankton.

In this study, we aim to analyze the clustering of planktonic swimmers under the influence of fluid inertial torque. We model plankton as point-like spherical microswimmers undergoing gravity sedimentation. We use direct numerical simulations of swimmers in homogeneous isotropic turbulence to analyze their clustering characteristic. In Sect. 2.1, we describe the model and the numerical approaches. In Sect. 3, we investigate the clustering using Voronoï analysis and show the relation between clustering and preferential sampling of downwelling regions. In Sect. 4, we draw the conclusions of the present study.

2 Methods

2.1 Model of spherical swimmers

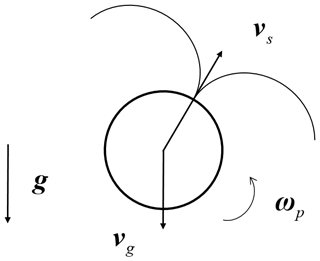
In the present study, we consider a spherical swimmer undergoing gravitational sedimentation, as shown in Fig. 1. The motion of plankton in fluid flows is usually described by a microswimmer model (Durham et al., 2009, 2013; Gustavsson et al., 2016; Lovecchio et al., 2019; Zhan et al., 2014), which assumes plankton to be a point-like microswimmer carried by a fluid flow. This assumption is justified when the Reynolds number, $\mathit{Re}=a|\mathit{v}-\mathit{u}|/\mathit{\gamma }$, is much smaller than unity. Here, the Reynolds number is defined based on the radius of a swimmer (a), the differences between the velocities of a swimmer (v) and the local undisturbed flow (u), and the kinematic viscosity of the fluid (γ). For typical plankton species, this assumption is justified because of their tiny size and limited motility, as summarized in our recent publication (Qiu et al., 2022a). For instance, the typical size and swimming speed of zooplankton are a=0.1 mm and $|\mathit{v}-\mathit{u}|=\mathrm{1.0}$ mm, respectively. Accordingly, we obtain Re=0.1 using the viscosity of water $\mathit{\gamma }={\mathrm{10}}^{-\mathrm{6}}$ mm² s⁻¹.

Figure 1 A sketch of a settling swimmer.

The dynamics of the swimmer is governed by the following expressions:

$$\begin{array}{}\text{(1)}& {\displaystyle }{m}_{\mathrm{p}}{\displaystyle \frac{\mathrm{d}\mathit{v}}{\mathrm{d}t}}=\mathrm{6}\mathit{\pi }a\mathit{\gamma }{\mathit{\rho }}_{\mathrm{f}}(\mathit{u}-\mathit{v})+m_{\mathrm{p}}\left(\mathrm{1}-{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{f}}}{{\mathit{\rho }}_{\mathrm{p}}}}\right)\mathit{g}+F_{\mathrm{s}}\mathit{n},\text{(2)}& {\displaystyle }\begin{array}{rl}{\displaystyle }{m}_{\mathrm{p}}{I}_{\mathrm{p}}{\displaystyle \frac{\mathrm{d}{\mathit{\omega }}_{\mathrm{p}}}{\mathrm{d}t}}=& {\displaystyle }\mathrm{6}\mathit{\pi }a{\mathit{\rho }}_{\mathrm{f}}\mathit{\gamma }C\left({\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\omega }-{\mathit{\omega }}_{\mathrm{p}}\right)\\ {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\mathrm{9}{m}_{\mathrm{p}}{\mathit{\rho }}_{\mathrm{f}}}{\mathrm{8}{\mathit{\rho }}_{\mathrm{p}}}}\left[\left(\mathit{v}-\mathit{u}\right)\times {\mathit{v}}_{\mathrm{s}}\right].\end{array}\end{array}$$

Here, m_p and ρ_p are the mass and the density of the swimmer, respectively. Equation (1) governs the translational motion of the swimmer, where the first term on the right-hand side denotes the Stokes drag. Here, ρ_f is the density of fluid. The second term represents the gravity and buoyancy on the swimmers due to gravity acceleration (g). The third term represents a swimming force (F_s) in the direction of the head of the swimmer, denoted as n. Meanwhile, Eq. (2) governs the rotation of the swimmer, where $I_{\mathrm{p}}=\mathrm{2}{a}^{\mathrm{2}}/\mathrm{5}$ denotes the moment of inertia per unit mass and ω_p represents the angular velocity of the swimmer. The first term on the right-hand side of Eq. (2) represents the Jeffery torque (Jeffery, 1922), where $C=\mathrm{4}{a}^{\mathrm{2}}/\mathrm{3}$, and ω is the vorticity of the fluid flow. The second term represents the fluid inertial torque experienced by a squirmer (Candelier et al., 2022), where v_s represents the swimming speed of the squirmer in a quiescent fluid. The model of fluid inertial torque is derived in the limit of Re→0, but it has been shown to be justified when Re<0.3 (Candelier et al., 2022), within the typical range of plankton physical properties (Qiu et al., 2022a).

Using the characteristic scales for velocity and time of the flow, u_f and τ_f, respectively, we make Eqs. (1) and (2) dimensionless:

$$\begin{array}{}\text{(3)}& {\displaystyle }\mathit{St}{\displaystyle \frac{\mathrm{d}{\mathit{v}}^{\prime }}{\mathrm{d}{t}^{\prime }}}={\mathit{u}}^{\prime }-{\mathit{v}}^{\prime }+{\mathrm{\Phi }}_{\mathrm{s}}\mathit{n}+{\mathrm{\Phi }}_{\mathrm{g}}{\mathit{e}}_{\mathrm{g}},\text{(4)}& {\displaystyle }\mathit{St}{\displaystyle \frac{I_{\mathrm{p}}}{C}}{\displaystyle \frac{\mathrm{d}{\mathit{\omega }}_{\mathrm{p}}^{\prime }}{\mathrm{d}{t}^{\prime }}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\omega }}^{\prime }-{\mathit{\omega }}_{\mathrm{p}}^{\prime }+{\displaystyle \frac{\mathrm{3}{\mathit{\tau }}_{\mathrm{f}}{u}_{\mathrm{f}}^{\mathrm{2}}}{\mathrm{16}\mathit{\gamma }}}\left[\left({\mathit{u}}^{\prime }-{\mathit{v}}^{\prime }\right)\times {\mathrm{\Phi }}_{\mathrm{s}}\mathit{n}\right],\end{array}$$

where the quantities with primes are dimensionless. In the above equations, the Stokes number $\mathit{St}=\left(\mathrm{2}{a}^{\mathrm{2}}{\mathit{\rho }}_{\mathrm{p}}\right)/\left(\mathrm{9}\mathit{\gamma }{\mathit{\rho }}_{\mathrm{f}}{\mathit{\tau }}_{\mathrm{f}}\right)$ reflects the inertia of the swimmer relative to the fluid of the same mass. ${\mathrm{\Phi }}_{\mathrm{s}}=v_{\mathrm{s}}/u_{\mathrm{f}}$ and ${\mathrm{\Phi }}_{\mathrm{g}}=\mathrm{2}({\mathit{\rho }}_{\mathrm{p}}/{\mathit{\rho }}_{\mathrm{f}}-\mathrm{1})a^{\mathrm{2}}g/\left(\mathrm{9}\mathit{\gamma }{u}_{\mathrm{f}}\right)$ are the dimensionless swimming and settling speeds, respectively. Typically, the St values of planktonic microswimmers are usually negligibly small, as summarized in Qiu et al. (2022a). For instance, using a=0.1mm, ${\mathit{\rho }}_{\mathrm{p}}/{\mathit{\rho }}_{\mathrm{f}}=\mathrm{1.05}$, and a typical range for the turbulence Kolmogorov timescale τ_f=31.6 to 1.0 s calculated from a typical dissipation rate (Kiørboe and Enric, 1995), one obtains $\mathit{St}=\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{4}}$ to $\mathrm{2.3}\times {\mathrm{10}}^{-\mathrm{3}}$. In such a limit, the left-hand sides of the Eqs. (3) and (4) can be neglected, and the dynamics simplifies to

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}{\mathit{x}}^{\prime }}{\mathrm{d}{t}^{\prime }}}={\mathit{v}}^{\prime },\text{(6)}& {\displaystyle \frac{\mathrm{d}\mathit{n}}{\mathrm{d}{t}^{\prime }}}={\mathit{\omega }}_{\mathrm{p}}^{\prime }\times \mathit{n},\text{(7)}& {\displaystyle }{\mathit{v}}^{\prime }={\mathit{u}}^{\prime }+{\mathrm{\Phi }}_{\mathrm{s}}\mathit{n}+{\mathrm{\Phi }}_{\mathrm{g}}{\mathit{e}}_{\mathrm{g}},\text{(8)}& {\displaystyle }{\mathit{\omega }}_{\mathrm{p}}^{\prime }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\omega }}^{\prime }+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathrm{\Psi }}_I}}\left({\mathit{e}}_{\mathrm{g}}\times \mathit{n}\right).\end{array}$$

Here, ${\mathrm{\Psi }}_I=\mathrm{8}\mathit{\gamma }/\left(\mathrm{3}{\mathit{\tau }}_{\mathrm{f}}{u}_{\mathrm{f}}^{\mathrm{2}}{\mathrm{\Phi }}_{\mathrm{s}}{\mathrm{\Phi }}_{\mathrm{g}}\right)$. The last term of Eq. (8) indicates that fluid inertial torque drives a squirmer swimmer to swim against gravity. Here, we use a dimensionless timescale Ψ_I to quantify the effect of fluid inertial torque. Ψ_I can be understood as the dimensionless time in which a swimmer in still fluid restores upward orientation from an inclined orientation under a reorientation torque. This is identical to the gyrotactic effect induced by bottom-heaviness, which is typically expressed as $\left(\mathrm{2}\mathrm{\Psi }{)}^{-\mathrm{1}}\right({\mathit{e}}_{\mathrm{g}}\times \mathit{n})$ (Kessler, 1986). However, we note that they are two different mechanisms. The gyrotactic torque on a bottom-heavy cell depends on the distance of the offset between the center of gravity and the hydrodynamic forces on a cell, which is usually determined by morphology. On the contrary, the fluid inertial torque is due to the fluid motion disturbed by the swimming and settling behavior of the cell and, thus, determined by motility.

In turbulence, we can take the respective turbulence Kolmogorov velocity and timescales u_η and τ_η as the characteristic scales of the flow. Using the relation $\mathit{\gamma }=u_{\mathit{\eta }}^{\mathrm{2}}{\mathit{\tau }}_{\mathit{\eta }}$, Ψ_I can be simplified as follows:

$$\begin{array}{}\text{(9)}& {\mathrm{\Psi }}_I={\displaystyle \frac{\mathrm{8}}{\mathrm{3}{\mathrm{\Phi }}_{\mathrm{s}}{\mathrm{\Phi }}_{\mathrm{g}}}}.\end{array}$$

The typical value of Φ_s and Φ_g of plankton can be estimated with their swimming and settling speeds as well as the Kolmogorov velocity scale of ocean turbulence. As summarized in Qiu et al. (2022a), the swimming speeds of different species vary from 200 to 1500 µm s⁻¹, while the settling speeds vary from 10 to 200 µm s⁻¹. The Kolmogorov velocity scale of ocean turbulence can be estimated from the typical dissipation rate $\mathit{ϵ}={\mathrm{10}}^{-\mathrm{9}}$ to 10⁻⁶ m² s⁻³ (Kiørboe and Enric, 1995), yielding $u_{\mathit{\eta }}=(\mathit{\gamma }\mathit{ϵ}{)}^{\mathrm{1}/\mathrm{4}}=\mathrm{178}$ to 1000 µm s⁻¹ with $\mathit{\gamma }={\mathrm{10}}^{-\mathrm{6}}$ m² s⁻¹. Based on these estimations, we consider a typical parameter space of $\mathrm{0}<{\mathrm{\Phi }}_{\mathrm{s}}<\mathrm{10}$ and $\mathrm{0}<{\mathrm{\Phi }}_{\mathrm{g}}<\mathrm{1}$. Large Φ_s and Φ_g are reached by swimmers with strong motility in weak turbulence where u_η is small. In such a case, the assumptions of our model are still justified. First, Re can still be small for plankton that swim fast, as long as their size is sufficiently small. Second, St is independent of plankton motility, which has been shown to be negligibly small for typical turbulence conditions in the ocean (Qiu et al., 2022a).

2.1.1 Direct numerical simulations of swimmers in turbulence

The motion of swimmers in homogeneous isotropic turbulence is simulated by Eulerian–Lagrangian direct simulations. The flow field is resolved in the Eulerian frame, while the motions of individual swimmers are solved along the Lagrangian trajectories using local flow information at swimmers' positions. The incompressible turbulent flow is directly simulated by solving the Navier–Stokes equations:

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{\partial \mathit{u}}{\partial t}}+\mathit{u}\cdot \mathrm{\nabla }\mathit{u}=-{\displaystyle \frac{\mathrm{\nabla }{p}_{\text{f}}}{{\mathit{\rho }}_{\mathrm{f}}}}+\mathit{\gamma }{\mathrm{\nabla }}^{\mathrm{2}}\mathit{u}+\mathit{f},\text{(11)}& {\displaystyle }\mathrm{\nabla }\cdot \mathit{u}=\mathrm{0},\end{array}$$

where p_f is the pressure of fluid. An external force f is applied to sustain turbulence and balance the rate of viscous dissipation at the Kolmogorov-scale η. The force is applied to the large-scale motion using the scheme proposed by Machiels (1997). Periodic boundary conditions are applied on all boundaries of the cubic domain with a size of (2π)³. We use a pseudo-spectral method to solve the Navier–Stokes equations, and we adopt the “$\mathrm{3}/\mathrm{2}$ rule” for reducing the aliasing error on the nonlinear term. The separation between turbulent motion of large and small scales is quantified by the Taylor Reynolds number ${\mathit{Re}}_{\mathit{\lambda }}=u_{\text{rms}}{L}_{\mathit{\lambda }}/\mathit{\gamma }$, where u_rms is the root-mean-square velocity and $L_{\mathit{\lambda }}=u_{\text{rms}}\sqrt{\mathrm{15}\mathit{\gamma }{\mathit{ϵ}}^{-\mathrm{1}}}$. In the present study, we consider a turbulence of Re_λ=60. To resolve the turbulent flow down to the Kolmogorov scale, we use 96³ grid points, which allows the maximum wave number resolved to be 1.78 times greater than the Kolmogorov wave number to ensure the accuracy of resolution even at Kolmogorov scales (Pope, 2000). The initial flow field is set as a random flow with an exponential energy spectrum, and an explicit second-order Adams–Bashforth scheme is used for time integration of Eqs. (10) and (11) with a time step smaller than 0.01τ_η (Rogallo, 1981).

Swimmers are initialized with random positions and orientations after turbulence is fully developed. When solving the trajectories of swimmer, fluid velocity and its gradients at Eulerian grid points are interpolated by a second-order Lagrangian method at the positions of swimmers. Equations (5) and (6) are integrated using the same second-order Adams–Bashforth scheme as the fluid phase. For each parameter configuration, 10⁵ swimmers are simulated, and the statistics are obtained by making an ensemble average over more than 80 uncorrelated time samples after the dynamics has reached a steady state.

3 Results

The instantaneous location and orientation of swimmers are depicted in Fig. 2. When swimmers are not settling (Fig. 2a), they are distributed randomly with a random orientation. Spherical swimmers are known to exhibit a random orientation due to the random fluid vorticity of turbulence. As a result, their motions in turbulence remain random and no cluster is formed. However, when swimmers are settling under the influence of the gravity (Fig. 2b), they tend to swim upwards and form clusters due to the contribution of fluid inertial torque. As discussed earlier, the fluid inertial torque on a settling swimmer induces an effect equivalent to the gyrotaxis mechanism. Gyrotactic swimmers are known to form spatial clusters and preferentially sample regions with downwelling or upwelling fluid velocity. Previous studies have documented that these phenomena depend on the swimming speed, reorientation time, and the shape of swimmers (Durham et al., 2013; Zhan et al., 2014; Gustavsson et al., 2016; Borgnino et al., 2018). However, in these studies, the reorientation time is determined by bottom-heaviness, which is independent of either swimming or settling speeds. Here, a reorientation effect is induced by fluid inertial torque with a timescale Ψ_I, which depends on the swimming and settling speeds of swimmers. Ψ_I cannot be treated as an independent parameter as earlier studies did (Durham et al., 2013; Zhan et al., 2014; Gustavsson et al., 2016; Borgnino et al., 2018). Hence, the picture of clustering may differ from previous studies, and it is worth further investigation.

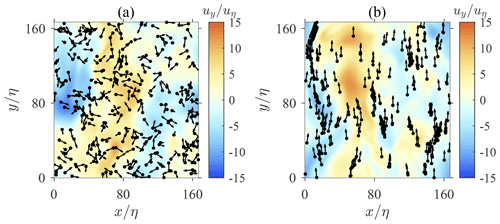
Figure 2 Instantaneous spatial distribution of swimmers in homogeneous isotropic turbulence. Black dots and tiny arrows represent the position and swimming direction of each swimmer, respectively. Background contour represents the vertical fluid velocity u_y. Panel (a) shows non-settling swimmers (Φ_g=0, Φ_s=10), whereas panel (b) shows settling swimmers (Φ_g=1, Φ_s=10).

3.1 Clustering

The clustering of swimmers is quantified by a three-dimensional Voronoï tessellation (Nilsen et al., 2013; Monchaux et al., 2010). The whole domain is divided into many Voronoï polyhedrons based on the positions of swimmers, with each polyhedron containing one swimmer. Any point in a polyhedron is closest to the corresponding swimmer among all swimmers. The volume of a Voronoï polyhedron is smaller when the corresponding swimmer is surrounded by more other swimmers, and vice versa. Therefore, the distribution of Voronoï polyhedron volumes quantifies the clusters of swimmers.

We use the MATLAB toolbox “voronoi.m” and “convhull.m” functions to compute the vertices of Voronoï polyhedrons and calculate their volumes. Figure 3a shows the probability distribution function (PDF) of Voronoï volumes for swimmers with different settling speeds. The PDF of Voronoï volumes of non-settling swimmers remains the same as the one generated from random positions, indicating the absence of clustering. When the settling speed increases, the PDFs become skewed and a peak at small $V/\langle V\rangle$ appears. This indicates the occurrence of clustering, because swimmers in clusters remain close to each other and their Voronoï volumes are thus small. Settling swimmers form clusters due to the effect of fluid inertial torque. As shown in Eq. (8), the fluid inertial torque drives settling swimmer to orient upward with a finite reorientation timescale Ψ_I. This is the same as the effect of bottom-heaviness (Kessler, 1986) which also drives swimmers to orient upward with a timescale Ψ dependent on the offset of the center of gravity with the center of hydrodynamic forces. For inertial torque, however, the timescale Ψ_I is inversely proportional to both the settling and swimming speeds of the swimmer.

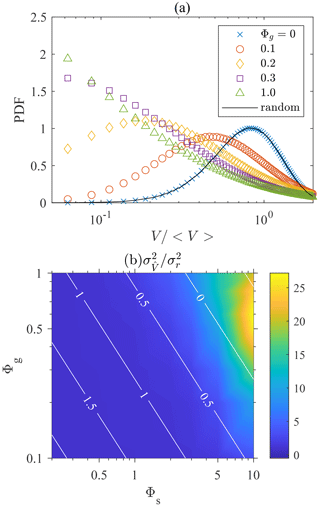
Figure 3 (a) Probability distribution function (PDF) of the volumes of Voronoï cells, normalized by the mean volume 〈V〉. Φ_s=10. (b) Variance of Voronoï volumes ${\mathit{\sigma }}_{\widehat{V}}^{\mathrm{2}}=E(V/\langle V\rangle -\mathrm{1}{)}^{\mathrm{2}}$ normalized by the value of randomly distributed particles. The white contour lines represent the value of log ₁₀Ψ_I in the parameter space.

To show how clustering depends on the settling and swimming speeds, we depict the variance of Voronoï volumes for different Φ_g and Φ_s in Fig. 3b. The corresponding magnitude of log ₁₀Ψ_I is also shown by white contour lines. We calculate the Voronoï volume of each swimmer and obtain the variance of the volume distribution normalized by the mean volume of each swimmer, ${\mathit{\sigma }}_{\widehat{V}}^{\mathrm{2}}=E(V/\langle V\rangle -\mathrm{1}{)}^{\mathrm{2}}$. The variance of Voronoï volumes quantifies the intensity of clustering because a stronger clustering results in a less uniform distribution of Voronoï volumes with larger variance. Figure 3b shows that clustering becomes stronger with increasing Φ_s and Φ_g, reaching a peak at Φ_g≈0.5 and Φ_s≈10. Further increasing Φ_g leads to a drop in the clustering intensity. This trend can be explained using the dimensionless reorientation timescale Ψ_I, which is inversely proportional to Φ_s and Φ_g (Eq. 9). When Ψ_I is zero, gyrotaxis is infinitely strong, causing swimmers to swim straight up against gravity, yielding $\mathit{n}=-{\mathit{e}}_{\mathrm{g}}$. As the fluid is incompressible, according to Eq. (7), the velocity field of swimmers has zero divergence, $\mathrm{\nabla }\cdot \mathit{v}=\mathrm{\nabla }\cdot \mathit{u}=\mathrm{0}$, indicating that no clustering is formed. When Ψ_I is infinitely large, the fluid inertial torque is negligible and the swimming direction is entirely determined by turbulent shear and becomes random, resulting in no clustering. Therefore, maximal clustering is expected to occur at a finite Ψ_I. Durham et al. (2013) observed that the intensity of the clustering of gyrotactic swimmers reaches its maximal when Ψ is of the order of unity (Durham et al., 2013). As Ψ_I is analogous to Ψ, the maximal clustering in the present case is also observed at a certain Φ_s and Φ_g that yields Ψ_I∼1.

3.2 Preferential sampling of downwelling regions

The clustering of spherical gyrotactic swimmers in turbulence has been shown to be associated with the preferential sampling of downwelling regions (Durham et al., 2013). Figure 4 shows the mean vertical fluid velocity at the position of swimmers. Swimmers always sample downwelling regions, and the maximal sampling occurs at large Φ_s but moderate Φ_g, which yields Ψ_I≈1. This observation clearly agrees with Durham et al. (2013), in which the maximal preferential sampling is also reached when Ψ≈1.

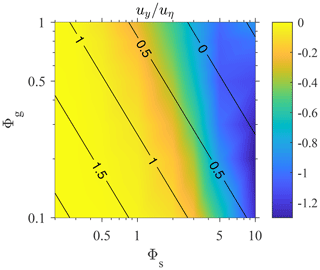
Figure 4 Mean vertical fluid velocity at swimmers' positions, 〈u_y〉, normalized by u_η as a function of Φ_g and Φ_s. The black contour lines represent the value of log ₁₀Ψ_I in the parameter space.

Comparing Figs. 4 and 3b, we observed a very similar trend between the sampling of downwelling regions and the intensity of clustering. The magnitude of both quantities increases with Φ_s, and maximal values are reached at a large Φ_s and a moderate Φ_g. This supports the theory that clustering occurs in downwelling regions (Durham et al., 2013; Fouxon and Leshansky, 2015; Gustavsson et al., 2016). Durham et al. (2013) showed that the divergence of the swimmer velocity field is $\mathrm{\nabla }\cdot \mathit{v}\propto -{\mathrm{\nabla }}^{\mathrm{2}}{u}_y$. As the ∇²u_y is negatively correlated to u_y in incompressible, homogeneous isotropic turbulence, the sinks of the swimmer velocity field tend to be located in downwelling regions with u_y<0. Here, we provide more direct evidence of clustering in downwelling regions.

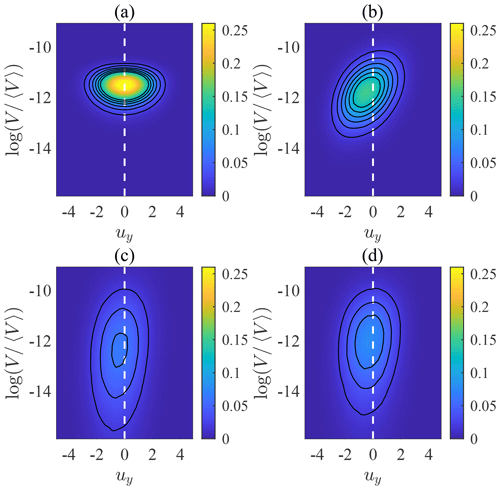
Voronoï analysis allows us to track the Voronoï volume of each swimmer. Based on the values of volumes, we can distinguish whether each swimmer is inside a cluster (with a small Voronoï volume) or located away from other swimmers (with a large Voronoï volume). Figure 5 shows the joint probability distribution function (joint PDF) of u_y and $\log (V/\langle V\rangle )$ for swimmers with different settling speeds. When Φ_g=0 (Fig. 5a), fluid inertial torque vanishes and swimmers do not preferentially sample downwelling regions, resulting in a symmetric joint PDF with respect to u_y=0. Moreover, because non-settling swimmers do not form clusters and their Voronoï volumes tend to be uniform, the joint PDF along $\log (V/\langle V\rangle )$ is concentrated at the peak. However, when Φ_g>0, the joint PDF becomes asymmetric with respect to u_y (Fig. 5b). The peak shifts towards u_y<0 because swimmers preferentially sample downwelling regions. Moreover, $\log (V/\langle V\rangle )$ tends to be smaller when u_y<0, indicating that swimmers in downwelling regions are more likely to form clusters. When the settling speed increases to Φ_g=0.5 (Fig. 5c), the joint PDF becomes flattened along $\log (V/\langle V\rangle )$, because the intensity of clustering reaches its maximal (see Fig. 3b), making it more probable for swimmers to have both smaller and larger Voronoï volumes. Furthermore, the joint PDF becomes less asymmetric with respect to u_y, indicating that strong clustering no longer occurs only in downwelling regions. When Φ_g further increases to Φ_g=1, the distribution becomes slightly concentrated again because the intensity of clustering is weakened compared with the case of Φ_g=0.5. In general, the joint PDFs reveal that swimmers are more likely to form cluster in downwelling regions, but when clustering is intense, the bias is weak.

Figure 5 Joint probability distribution function (PDF) of the vertical fluid velocity u_y and the Voronoï volumes $\log (V/\langle V\rangle )$. Φ_s=10 for all panels. White dashed lines correspond to u_y=0. (a) Φ_g=0. (b) Φ_g=0.2. (c) Φ_g=0.5. (d) Φ_g=1.0.

4 Conclusions

A settling spherical squirmer experiences a fluid inertial torque that causes it to swim against gravity, acting as an effective gyrotactic torque (Candelier et al., 2022). While previous studies have focused on gyrotactic torque originating from bottom-heaviness, the role of fluid inertial torque has been neglected (Durham et al., 2013; Zhan et al., 2014; Gustavsson et al., 2016; Borgnino et al., 2018). In the present study, we modeled an inertia-less microswimmer under the influence of fluid inertial torque. The magnitude of the torque is quantified using a dimensionless reorientation timescale Ψ_I which is proportional to the inverse of the dimensionless swimming speed (Φ_s) and settling speed (Φ_g).

Using direct numerical simulation, we investigated the clustering of swimmers under fluid inertial torque. We quantified the clustering using Voronoï analysis. When swimmers are not settling, the fluid inertial torque vanishes and the swimmers are randomly distributed, resulting from a random swimming direction, with no clustering observed. Settling swimmers experience a fluid inertial torque and behave similarly to gyrotactic swimmers. We observed that swimmers form more intense clustering when Φ_s and Φ_g become larger, with maximal clustering intensity occurring at the largest Φ_s and a modest Φ_g, corresponding to Ψ_I∼1.

We also examined how the clustering of spherical swimmers is related to their preferential sampling of downwelling regions. We found that when swimmers are not settling, their dynamics remains isotropic and no preferential sampling is observed in the gravity direction. However, the fluid inertial torque and the settling speed break this symmetry and drive settling swimmers to sample downwelling regions. The sampling is more pronounced with larger Φ_s and Φ_g, reaching the maximum when Ψ_I≈1. The trend of preferential sampling shows a similar pattern to that of clustering intensity, indicating a correlation between the two phenomena. We used the joint PDF of Voronoï volumes and local vertical fluid velocity to demonstrate that swimmers tend to form clusters in downwelling regions.

The fluid inertial torque on settling swimmers can cause the formation of small-scale clusters, highlighting the importance of fluid inertial effects on the dynamics of plankton. However, most earlier studies did not consider gravitational sedimentation, leading to the neglect of fluid inertial torque. This results in an underestimate of the intensity of gyrotaxis, as the total gyrotactic torque is contributed by both fluid inertial torque and bottom-heaviness. In addition, the fluid inertial torque is proportional to the swimming and settling speeds, making the reorientation time a dependent parameter. Therefore, planktonic swimmers have the potential to tune their reorientation behavior and, thus, control clustering intensity by adjusting their swimming speed, which further impacts their mating, predation, and feeding.

Finally, it is necessary to clarify the assumptions of our model. First, we considered only spherical swimmers. Nonspherical plankton, such as elongated ones, probably experience a fluid inertial torque stemming from both their nonspherical shape (Dabade et al., 2015; Sheikh et al., 2020; Gustavsson et al., 2019; Qiu et al., 2022a) and propulsion mechanism (Candelier et al., 2022). While the analytical solution for the fluid inertial torque on a nonspherical swimmer remains unclear, fully resolved numerical simulation could be used to reveal the dynamics of nonspherical settling swimmers. The resulting findings could be potentially applied to the model of point-like swimmer. The second assumption is that we neglected the inertia of the microorganisms by assuming St→0. Under this assumption, the dynamics (3) and (4) are simplified into a kinematic model (Eqs. 5–8). This is usually adequate for small microorganisms. For instance, St for some typical marine plankton species ranges from 10⁻⁷ to 10⁻³ (Qiu et al., 2022a). However, the St of large organisms in a relatively quiescent flow can be potentially too large to ignore the inertia of microorganisms. In such case, the full dynamics (3) and (4) must be considered, and the effect of the inertia of microorganisms needs further investigation in future studies.