Mahalanobis distance-based recognition of changes in the dynamics of a seismic process

In the present work, we aim to analyse the regularity of a seismic process based on its spatial, temporal, and energetic characteristics. Increments of cumulative times, increments of cumulative distances, and increments of cumulative seismic energies are calculated from an earthquake catalogue for southern California from 1975 to 2017.

As the method of analysis, we use the multivariate Mahalanobis distance calculation, combined with a surrogate data testing procedure that is often used for the testing of non-linear structures in complex data sets. Before analysing the dynamical features of the seismic process, we tested the used approach for two different 3-D models in which the dynamical features were changed from more regular to more randomised conditions by adding a certain degree of noise.

An analysis of the variability in the extent of regularity of the seismic process was carried out for different completeness magnitude thresholds.

The results of our analysis show that in about a third of all the 50-data windows the original seismic process was indistinguishable from a random process based on its features of temporal, spatial, and energetic variability. It was shown that prior to the occurrence of strong earthquakes, mostly in periods of generation of relatively small earthquakes, the percentage of windows in which the seismic process is indistinguishable from a random process increases (to 60 %–80 %). During periods of aftershock activity, the process of small earthquake generation became regular in all of the windows considered, and thus was markedly different from the randomised catalogues.

In some periods within the catalogue, the seismic process appeared to be closer to randomness, while in other cases it became closer to a regular behaviour. More specifically, in periods of relatively decreased earthquake generation activity (with low energy release), the seismic process appears to be random, while during periods of occurrence of strong events, followed by series of aftershocks, significant deviation from randomness is shown, i.e. the extent of regularity markedly increases. The period for which such deviation from random behaviour lasts depends on the amount of seismic energy released by the strong earthquake.

1 Introduction

The process of earthquake generation remains a focus of diverse interdisciplinary investigations by Earth science researchers worldwide. The practical and scientific reasons for this interest are well known and easily explainable. However, despite this strong interest and the enormous research efforts that have already been applied, many important aspects of the complex seismic process characterised by space and time clustering are still not clear (Bowman and Sammis, 2004; Godano and Tramelli, 2016; Kossobokov and Nekrasova, 2017; Matcharashvili et al., 2018; Pasten et al., 2018).

One of the fundamental questions of modern Earth science concerns the dynamics of the seismic process. As a logical compromise between the different approaches that have been proposed for this problem, it has been suggested that the dynamical features of the seismic process may vary, ranging from periodic (primarily for large events) to the totally random occurrence of earthquakes (Matcharashvili et al., 2000; Corral, 2004; Davidsen and Goltz, 2004). The same, in terms of the concept of intermittent criticality of earthquake generation, can be expressed as the ability of a tectonic system to approach and/or retreat from the critical state, i.e. the state of the system in which strong earthquakes occur (see e.g. Sornette and Sammis, 1995; Bowman et al., 1998; Bowman and Sammis, 2004; Corral, 2004).

Current knowledge of the scaling and memory characteristics of the overall seismic process indeed supports this proposed diversity in the dynamics of earthquake generation (Sornette and Sammis, 1995; Bowman et al., 1998; Abe und Suzuki, 2004; Chelidze and Matcharashvili, 2007; Czechowski, 2001, 2003; Białecki and Czechowski, 2010; Kossobokov and Nekrasova, 2017). Moreover, the results of analyses carried out to assess the dynamical features of the seismic process in terms of its separate domains (time, space, and energy) also indicate differences in behaviour (see e.g. Goltz, 1998; Matcharashvili et al., 2000, 2002; Abe and Suzuki, 2004; Chelidze and Matcharashvili, 2007; Iliopoulos et al., 2012). More specifically, it has been shown that the seismic process in the temporal and spatial domains may reveal features that are close to so-called low-dimensional dynamical structures, although the features of the behaviour in the energy domain appear close to randomness, i.e. representing high-dimensional dynamical processes (Goltz, 1998; Matcharashvili et al., 2000; Iliopoulos et al., 2012). This has been shown for whole catalogues as well as for their parts and for different time periods.

Coming back to the concept of a critical state, it should be emphasised that intermittent criticality implies time-dependent variations in the activity during a seismic cycle. Thus, since the critical state is usually described as the state of the system when it is at the boundary between order and disorder (Bowman et al., 1998), we can describe the time variability of the seismic process in terms of the contemporary concept of geocomplexity (Rundle et al., 2000).

According to present knowledge, and in complete accordance with the concept of intermittent criticality, it is accepted that the extent of regularity (order) of the seismic process may vary in all its domains (temporal, spatial, and energetic) (Goltz, 1998; Abe and Suzuki, 2004; Chelidze and Matcharashvili, 2007; Iliopoulos et al., 2012; Matcharashvili et al., 2000, 2002, 2018). At the same time, despite the large number of recent publications demonstrating the diversity of these changes in the dynamics of the seismic process, interest in this issue continues to grow. In this context, it should be emphasised that it is important to assess these dynamical changes on the basis of multivariate analysis, taking into account all the temporal, spatial, and energetic constituents of the seismic process. Thus, one important research task is to understand the character of these changes in the entire seismic process.

Based on the state-of-the-art studies mentioned above, we aim in the present work to investigate the dynamical features of the seismic process based on all its temporal, spatial, and energetic characteristics. We carry out a multivariate comparison of the seismic process using an original earthquake catalogue for southern California and a set of randomised catalogues in which unique (temporal, spatial, and energetic) dynamical structures have been intentionally distorted by a shuffling procedure. This multivariate comparison of an original catalogue with randomised catalogues may help us to gain new knowledge about the character of the changes that occur in the extent of order/disorder of the seismic process. In addition, we will have stronger arguments regarding where and how the dynamics of the original seismic process in the analysed catalogue was close to disorder (irregularity) or order (regularity). We also aim to determine whether such changes are related to the process of preparation for strong earthquakes.

The results obtained in our research show that the extent of regularity in the analysed seismic process changes and is closer to randomness in the periods prior to strong earthquakes. After strong earthquakes, the regularity of the original seismic process assessed based on its temporal, spatial, and energetic characteristics is clearly increased.

2 Data used

We based our analysis on the southern California (SC) earthquake catalogue, which is available from http://www.isc.ac.uk/iscbulletin/search/catalogue/ (last access: November 2018). We focused on the time period from 1975 to 2017 (see Fig. 1). According to results of a time completeness analysis, the SC earthquake catalogue for the considered period is complete for M=2.6.

Figure 1 Map of the area covered by the southern California earthquake catalogue (1975–2017).

As pointed out above, we aimed to carry out a multivariate analysis of the dynamical features of the seismic process. Thus, in order to preserve the original character of the temporal, spatial, and energetic characteristics of this process, we intentionally avoided any cleaning or filtering of the earthquake catalogue used here. This approach was based on a widely accepted practice (see e.g. Bak et al., 2002; Christensen et al., 2002; Corral, 2004; Davidsen and Goltz, 2004; Matcharashvili et al., 2018) in which all events are assumed to be on the same footing and the catalogue is considered as a whole. In other words, we did not pay attention to the details of tectonic features, the locations of the earthquakes, or their classification as mainshock or aftershock (Bak et al., 2002; Christensen et al., 2002; Corral, 2004).

3 Methods of analysis

In view of our research goal, i.e. a multivariate assessment of the extent of the regularity of the original seismic process, we need to analyse the seismic process in terms of the simultaneous variability in all three of its domains: temporal, spatial, and energetic. From this point of view, we consider cumulative sums of the characteristics of earthquakes in the temporal, spatial, and energetic domains (Fig. 2). The cumulative sum representation in the time domain is trivial, since time is already a cumulative characteristic, representing the cumulative sum of inter-earthquake times. Cumulative representation in the spatial domain is also quite feasible, and we consider cumulative sums of distances between consecutive earthquakes in the seismic catalogue. The cumulative sum of seismic energies released by consecutive earthquakes is also often used in the context of the different aspects of earthquake generation (e.g. Bowman et al, 1998; Bowman and Sammis, 2004; Nakamichi et al., 2018). Here, we add that despite some controversies (see e.g. Corral, 2004, 2008) over the question of the reliable energetic measurement of earthquake size, its relation to the magnitude of an earthquake is generally accepted. Thus, from the earthquake magnitudes in the SC catalogue, we can calculate the amount of seismic energy released, according to Kanamori (1977).

We start from the first earthquake in the catalogue (for the time period of interest, from 1975 to 2017), which we consider a starting point, and then follow the time sequence. Thus, ICT(i) is the ith interevent time (i.e. the time between the ith earthquake and the (i-1)th earthquake); ICD(i) is the distance between consecutive events and ICE(i) is the energy of the ith earthquake. We can also define these quantities in terms of increments of the cumulative sums; i.e. ICT(i), ICD(i), and ICE(i) are the increments of cumulative sums of the interevent times, interevent distances, and seismic energy released by consecutive earthquakes, respectively.

In order to have the same standard deviation for the three groups of data, the standard deviations were calculated for each of the ICT(i), ICD(i), and ICE(i) data sets, and the data sets were then normalised to have their standard deviations equal to 1.

In order to characterise the seismic process from a multivariate point of view, we used a well-known statistical test, the Mahalanobis distance (MD) calculation. Calculation of the MD is an effective multivariate method for different classification purposes and is often used for data sets of different origins. Thus, the objective of our analysis can be regarded as a classification task of the features of a seismic process, assessed using the variability in ICT(i), ICD(i), and ICE(i).

Figure 2 Cumulative sums of (a) interevent times; (b) inter-earthquake distances; and (c) released seismic energies, starting from the first event in the southern California catalogue (1975–2017).

In other words, we aimed to assess the changes that occurred in the seismic process over the period covered by the SC catalogue (1975–2017). It is well known that the correctness of a multivariate assessment and classification of a system is strongly dependent on correct feature extraction (McLachlan, 1992, 1999). In other words, the data sets used should be specifically focused on the targeted features of the process under investigation. Hence, in order to have data sets with a similar physical sense, enabling us to assess the dynamical features of seismicity in three domains, we used ICT(i), ICD(i), and ICE(i) data sets.

The MD (Mahalanobis, 1930; McLachlan, 1992, 1999) is a widely accepted method of measuring the separation of two groups of vectors (e.g. one group A, consisting of N_A vectors ${\mathit{a}}_i=(a_{ix},a_{iy},a_{iz}$), and another group B, with N_B vectors b_i). In this method, the difference between the groups can be considered in terms of the difference between the mean vectors 〈a_i〉 and 〈b_i〉 of each group relative to the common within-group variation. This allows us to draw a conclusion on whether the investigated groups are similar or dissimilar. The MD (often denoted as D) can be calculated from the following expression:

$$\begin{array}{}\text{(1)}& D^{\mathrm{2}}=\left(〈{\mathit{a}}_i〉-〈{\mathit{b}}_i〉\right){}^{\mathrm{T}}{\mathbf{S}}^{-\mathrm{1}}\left(〈{\mathit{a}}_i〉-〈{\mathit{b}}_i〉\right),\end{array}$$

where S is the pooled covariance matrix

$$\begin{array}{}\text{(2)}& \mathbf{S}={\displaystyle \frac{(N_{\mathrm{A}}-\mathrm{1}){\mathbf{S}}_{\mathrm{A}}+(N_{\mathrm{B}}-\mathrm{1}){\mathbf{S}}_{\mathrm{B}}}{N_{\mathrm{A}}+N_{\mathrm{B}}-\mathrm{2}}},\end{array}$$

and S_A, S_B are covariance matrices of the corresponding groups, e.g.

$$\begin{array}{}\text{(3)}& {\mathbf{S}}_{\mathrm{A}}={\displaystyle \frac{\mathrm{1}}{N_{\mathrm{A}}}}{\mathbf{X}}_{\mathrm{A}}^{\mathrm{T}}{\mathbf{X}}_{\mathrm{A}}.\end{array}$$

The superscripts “T” and “−1” denote the transpose and the inverse operators, respectively. The rows of matrix X_A (X_B) form the components of the N_A (N_B) vectors a_i(b_i), e.g.

$$\begin{array}{}\text{(4)}& {\mathbf{X}}_{\mathrm{A}}=\left[\begin{array}{ccc}{a}_{\mathrm{1}x}& a_{\mathrm{1}y}& a_{\mathrm{1}z}\\ \begin{array}{l}\mathrm{\dots }\\ \mathrm{\dots }\end{array}& \begin{array}{l}\mathrm{\dots }\\ \mathrm{\dots }\end{array}& \begin{array}{l}\mathrm{\dots }\\ \mathrm{\dots }\end{array}\\ a_{N_{\mathrm{A}}x}& a_{N_{\mathrm{A}}y}& a_{N_{\mathrm{A}}z}\end{array}\right].\end{array}$$

In general, two conditions or states of a system are more likely to fall into the same class or group (or have a higher probability of being similar) if the calculated MD value is smaller. In order to assess the significance of the difference between the groups, Hotelling's T² statistic was used, converted into an F value and assessed using an F test. The F value was calculated as follows:

$$\begin{array}{}\text{(5)}& F={\displaystyle \frac{N_{\mathrm{A}}{N}_{\mathrm{B}}(N_{\mathrm{A}}+N_{\mathrm{B}}-p-\mathrm{1})}{(N_{\mathrm{A}}+N_{\mathrm{B}})(N_{\mathrm{A}}+N_{\mathrm{B}}-\mathrm{2})p}}{D}^{\mathrm{2}}.\end{array}$$

In Eq. (5), p is the degrees of freedom. Then, in order to draw a final conclusion on the similarity or dissimilarity of the two groups, we compare the calculated F values with a critical value F_c (corresponding to the degrees of freedom). In the case where F>F_c, a statistically significant difference between the groups is established, with a specific probability (significance level).

When dealing with analysis of complex seismic processes, it needs to be pointed out that the MD calculation is sensitive to inter-variable changes in a multivariate system (Mahalanobis, 1930; Lattin et al., 2003) and that it takes into account the correlations between several variables providing information on the similarity or dissimilarity between the compared groups (Taguchi and Jugulum, 2002; Kumar et al., 2012).

If we are primarily interested in analysing dynamical changes occurring on short scales (short data sets), it is useful to combine the advantages of multivariate analysis and surrogate testing (Matcharashvili et al., 2017, 2018). In this case, we can use the multivariate MD calculation to examine whether the original seismic process is similar to or dissimilar from a random process (randomised catalogues) by comparing them based on the three main characteristics listed above.

In summary, we aim to analyse the way in which the order in the seismic process, as assessed using its derivative temporal, spatial, and energetic characteristics (the quantities ICT(i), ICD(i), and ICE(i)), changes over the period of analysis. To achieve this, we compare the original SC earthquake catalogue (1975–2017) with a set of artificial catalogues in which the original dynamical structures (of the temporal, spatial, and energetic distributions) have been intentionally destroyed by a shuffling procedure (Kantz and Schreiber, 1998). We generated 100 such randomised catalogues. In order to analyse the seismic process, we divided these catalogues into consecutive, non-overlapping 50-data windows shifted by 50 data. Thus, each window from the original catalogue represents group A, and each window from the shuffled catalogue forms a group B (we have a total of 100 B groups). For example, the vector ${\mathit{a}}_i=(a_{ix},a_{iy},a_{iz})=\left(\text{ICT}\right(i),\text{ICD}(i),\text{ICE}(i\left)\right)$.

4 Testing the method on models

In order to verify whether the approach used here, which combines MD calculation with surrogate testing, is indeed useful for discerning any changes occurring in the natural 3-D system (the seismic process in a tectonic system), with slightly or strongly different dynamical features, we used time series generated by two 3-D simulated systems with added noise. These were a 3-D Lorenz system and a crack fusion model with added Gaussian noise.

4.1 Lorenz model

The well-known Lorenz model describes the motion of an incompressible fluid contained in a cell that has a higher temperature at the bottom and a lower temperature at the top. Despite the simple form of this set of equations, very complex behaviour can be exhibited. This approach has therefore been commonly used to present the interesting non-linear dynamics of 3-D systems.

The Lorenz model has the following form (see e.g. Hilborn, 1994):

$$\begin{array}{}\text{(6)}& \begin{array}{l}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}=p(y-x),\\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}=-xz+rx-y,\\ {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}t}}=xy-bz,\end{array}\end{array}$$

where p represents the Prandtl number, r is the Rayleigh number, and b is related to the ratio of the vertical height of the fluid layer to the horizontal size of the convection rolls. For values of r<1, trajectories in 3-D space (x, y, z) are attracted by the origin (0, 0, 0). When r>0, the Lorenz model has three fixed points which can have different features.

In this work, we need time series that are close to stationary, and thus in order to avoid periodic orbits we assume r<1, namely r=0.7. In order to generate our time series, we use the discrete version of the Lorenz equations that are modified by the introduction of two random noise terms:

$$\begin{array}{}\text{(7)}& \begin{array}{l}{x}_{t+\mathrm{\Delta }t}=p(y_t-x_t)\mathrm{\Delta }t+x_t+c{\mathit{\xi }}_t+\mathit{\epsilon }{\mathit{\zeta }}_x,\\ y_{t+\mathrm{\Delta }t}=(-x_t{z}_t+r{x}_t-y_t)\mathrm{\Delta }t+y_t+c{\mathit{\xi }}_t+\mathit{\epsilon }{\mathit{\zeta }}_y,\\ z_{t+\mathrm{\Delta }t}=(x_t{y}_t-b{z}_t)\mathrm{\Delta }t+z_t+c{\mathit{\xi }}_t+\mathit{\epsilon }{\mathit{\zeta }}_z.\end{array}\end{array}$$

The first noise term, ξ, is the same (i.e. has the same value) in all three equations and for all cases under investigation. Due to fluctuations generated by the noise, the states of the system are around the attractor at the origin (0, 0, 0). The Lorenz model with only the ξ noise term will be treated as a basic reference system, i.e. a “deterministic” system. The second noise term ζ_x (ζ_y and ζ_z) is generated separately for each of the three equations. It is multiplied by the parameter ε whose values will increase. The role of the second noise term is to check the influence of increasing randomness on the measures of order in the process. To generate time series using the system in Eq. (5), we assume the following values for the parameters: p=10, r=0.7, $b=\mathrm{8}/\mathrm{3}$, and c=3. The initial values are (x(0), y(0), z(0)) $=(\mathrm{0},\mathrm{0},\mathrm{20})$ and the time step is Δt=0.001. The parameter ε increases from 0.0 (for the reference system) to 1.0.

4.2 Crack fusion model

The kinetic crack fusion model (Czechowski, 1991, 1993, 1995) describes the evolution of a system of numerous cracks which can nucleate, propagate, and coalesce under applied stress. Here, we use a simple version of the model (related to seismic processes) in which only three crack populations (small cracks x(t), medium cracks y(t), and large cracks z(t)) are taken into account. Their evolution is governed by the following system of non-linear equations:

$$\begin{array}{}\text{(8)}& \begin{array}{l}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}=-a(\mathrm{1}-k_x)xx-axy-axz+bz+\mathit{\mu }T,\\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}=a(k_y-k_x)xx-a(\mathrm{1}-k_y)yy-a(\mathrm{1}-\mathrm{2}{k}_y)xy-ayz,\\ {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}a(\mathrm{1}-\mathrm{2}{k}_y)(xx+\mathrm{2}xy+yy)-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}azz-gz,\end{array}\end{array}$$

where the parameters a,k_x, and k_y are related to the probability of coalescence, b is the nucleation rate of small cracks around large cracks, and g is the healing rate of large cracks. The second source term for small cracks is due to the external stress T(t), which can grow in response to relative tectonic plate motion and diminish according to the number of large cracks z(t), i.e.

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\mathrm{d}T}{\mathrm{d}t}}=\left\{\begin{array}{ll}v(\mathrm{1}-z)& T\ge \mathrm{0},\\ \mathrm{0}& T<\mathrm{0}.\end{array}\right.\end{array}$$

In a similar way to the Lorenz model, the crack fusion model exhibits two kinds of behaviour: it can decay to one stationary point or its attractor can be given by periodic orbits. As above, we need stationary-like time series, so in order to avoid periodic orbits, we assume the parameters $v\mathit{\mu }=\mathrm{1000}<(v\mathit{\mu }{)}_{\mathrm{crit}}=\mathrm{6320}$ and modify the hierarchical system by introducing two random noise terms ξ and ζ_x to the equation for small cracks only.

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{x}_{t+\mathrm{\Delta }t}=& (-a(\mathrm{1}-k_x)x_t{x}_t-a{x}_t{y}_t-a{x}_t{z}_t\\ & +b{z}_t+\mathit{\mu }{T}_t)\mathrm{\Delta }t+x_t+c{\mathit{\xi }}_t+\mathit{\epsilon }{\mathit{\zeta }}_x,\\ y_{t+\mathrm{\Delta }t}=& \left(a\right(k_y-k_x)x_t{x}_t-a(\mathrm{1}-k_y)y_t{y}_t\\ & -a(\mathrm{1}-\mathrm{2}{k}_y)x_t{y}_t-a{y}_t{z}_t)\mathrm{\Delta }t+y_t,\\ z_{t+\mathrm{\Delta }t}=& \left({\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}a(\mathrm{1}-\mathrm{2}{k}_y)(x_t{x}_t+\mathrm{2}{x}_t{y}_t+y_t{y}_t)\right.\\ & \left.-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}a{z}_t{z}_t-g{z}_t\right)\mathrm{\Delta }t+z_t.\end{array}\end{array}$$

In order to generate time series using the system of equations in Eq. (10), we assume the following values for the parameters: a=8, b=20, c=0.5, g=1, k_x=0.3, k_y=0.45, v=10, μ=100, initial values (x(0), y(0), z(0)) $=(\mathrm{0},\mathrm{0},\mathrm{20})$, and time step Δt=0.01. The parameter ε increases from 0.0 (for the reference system) to 0.35.

Thus, in order to ensure that the multivariate method used here enables us to discriminate between different conditions of dynamical systems, we use 3-D models in which the dynamical features are changed from more regular to more randomised conditions by adding some extent of noises. We start with the Lorenz system (Fig. 3) and then proceed to the crack fusion model (Czechowski, 1991, 1993, 1995) (Fig. 4). As explained above, in both cases we add noises of different intensity to the original 3-D system, assuming that the more intense the added noise, the closer the model system is to randomness. Figures 3 and 4 clearly show that the number (or portion) of the 50-data windows in which the condition of the 3-D system is indistinguishable from the initial condition (the system with no added noise) gradually decreases when the intensity of the added noise is increased. This means that the method of analysis used here enables us to distinguish the conditions of systems even in cases when they are only slightly different (i.e. only a small amount of noise is added) (see the left-hand parts of the curves in Figs. 3 and 4, showing a smaller amount of added noise).

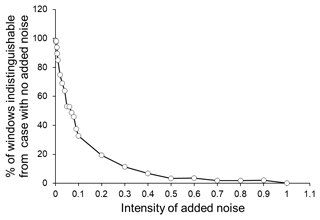
Figure 3 Percentage of the 50-data windows (shifted by 50 data steps) of the Lorenz system with added noise that are indistinguishable from the initial condition (system with no added noise).

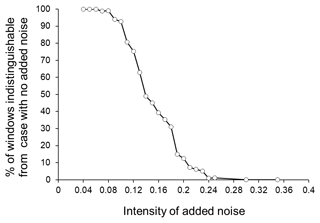
Figure 4 The percentage of the 50-data windows (shifted by 50 data steps) of the crack fusion model with added noise that are indistinguishable from the initial condition (system with no added noise).

For clarity, we note here that in Figs. 3 and 4, we show results for the case of windows 50-data long, since in the analysis of the seismic catalogue below, we also use this size of window. At the same time, it should be emphasised that the result of the above analysis depends on the timescale used (the size of the windows). For larger windows (500- or 1000-data long, for example) distinguishability from the starting condition (i.e. without added noise) requires a larger amount of added noise, although the general conclusion remains the same: the method of analysis used here enables us to distinguish between the states of 3-D systems with different extents (or degrees) of dynamical regularity.

5 Results and discussion

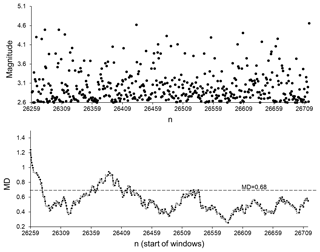
Having shown that the multivariate testing method selected for this research enables us to discriminate between different conditions of dynamical systems, we proceed to analyse data sets from the original seismic catalogue and the randomised catalogues mentioned above. We start from the case where MD values are calculated for non-overlapping, 50-data, windows shifted by 50 data steps, in the same way as for the 3-D model data sets. Figure 5 presents the results of this calculation. Groups consisting of the ICT(i), ICD(i), and ICE(i) columns from the original catalogue were compared with the corresponding three columns of ICT(i), ICD(i), and ICE(i) data from each of 100 randomised catalogues (shuffled in time, space, and by magnitudes). In this way, the MD(i) values were calculated. The MD values shown in Fig. 5 are averages of the MD(i) values calculated for each of the randomised catalogues. The dashed lines in this figure and the following figures indicate the critical value F_c, which was discussed in the previous section. For the number of degrees of freedom used in this research, F_c=3.99, corresponding to a significant difference between the groups with p=0.01 (MD =0.68 corresponds to F_c=3.99).

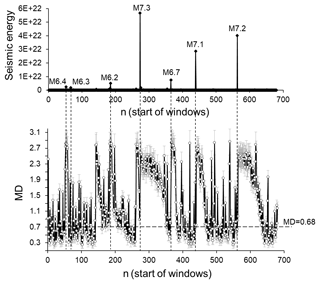
Figure 5 Seismic energy released (upper curve) and average MD values (bottom curve) calculated for consecutive non-overlapping 50-data windows shifted by 50 data steps, for the southern California earthquake catalogue (1975–2017). Averages of the MD values and the corresponding standard deviations (given in the lower plot by white circles and grey error bars) were calculated by comparing ICT(i), ICD(i), and ICE(i) sequences in the original catalogue and in the set of randomised catalogues. The dotted line corresponds to a significant difference between windows at p=0.01.

For a more precise analysis, we calculate the MD values for 50 data windows shifted by one data step (Fig. 6).

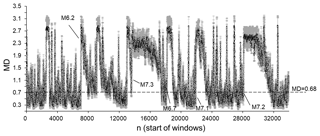
Figure 6 Average MD values calculated by comparing ICT(i), ICD(i), and ICE(i) sequences from the original SC catalogue and from the set of randomised catalogues. The dotted line corresponds to a significant difference between windows at p=0.01. MD values are calculated for 50 data windows shifted by one data step.

The results in Figs. 5 and 6 support the view that despite the generality of the background physics (Lombardi and Marzocchi, 2007; Di Toro et al., 2004; Davidsen and Goltz, 2004; Helmstetter, 2003; Helmstetter and Sornette, 2002; Corral, 2008), the processes taking place prior to and after main shocks are nevertheless different (Sornette and Knopoff, 1997; Davidsen and Goltz, 2004; Wang and Kuo, 1998). According to recent research, the latter is characterised by long- and short-range correlations and thus is more ordered, while the former is apparently more uncorrelated and random-like (Touati et al., 2009; Godano, 2015). Indeed, according to Bowman et al. (1998), the loss of energy (released also in the form of seismic energy) that is related to the occurrence of strong events introduces memory into the system (Bowman and Sammis, 2004).

We can see from Figs. 5 and 6 that in the SC earthquake catalogue considered here, the seismic process after strong earthquakes is more regular than in the periods prior to these events. Indeed, in all windows, the seismic process, as assessed based on the variability in ICT(i), ICD(i), and ICE(i), after strong earthquakes is significantly different from the randomised catalogues. In contrast, the majority of the 50-data windows examined here show that the original seismic process prior to strong earthquakes is statistically indistinguishable from the randomised catalogues (see Figs. 5 and 6). It is important to mention that the windows, located prior to strong earthquakes, make up 33 % of the total number of windows in the entire catalogue. Moreover, if we consider only those periods in the catalogue that immediately precede strong earthquakes, the proportion of windows in which the seismic process is indistinguishable from randomness increases to 60 %–80 %. Thus, in the overwhelming majority of windows that immediately precede strong earthquakes, the seismic process is indistinguishable from that observed in the randomised catalogues. The seismic process in these parts of the original catalogue can therefore be regarded as random-like.

In order to exclude the possibility that some of the characteristics selected here (ICT(i), ICD(i), and ICE(i)) may have more influence on the results than the others, we carried out a similar analysis comparing groups of original and randomised catalogues by two of the three characteristics. The results of this separate comparison of the groups, using pairs of columns (ICT(i) and ICD(i); ICT(i) and ICE(i); ICD(i) and ICE(i)), are not shown here, but generally coincide with the results of the above analysis (using all three columns). This indicates that the results of our analysis cannot be reduced to the influence of only a single characteristic. Thus, the changes shown in Figs. 5 and 6 reveal changes in the dynamical features of the seismic process as whole, involving changes in all three of its domains.

For better visualisation of the above results (see Fig. 6), Fig. 7 presents MD values calculated for 50 data windows for the period from 14 May 1990 (the window started from event 12100 in the SC catalogue) to 28 June 1992 (the window started from event 13797 in the SC catalogue). Within this period, two strong earthquakes occurred, M 6.1 (23 April 1992) and M 7.3 (28 June 1992). Prior to both of these strong earthquakes, we observe windows in which the seismic process is indistinguishable from the randomised catalogues in terms of the variation in ICT(i), ICD(i), and ICE(i) data (see circles below the dotted significant difference line). It is also noticeable that after these strong events, the extent of order in the seismic process strongly increases, as shown by the changes in MD values (the original catalogue becomes more different from the randomised catalogue). For M 7.3, unlike the M 6.1 event, this increase lasted for a considerable time after the strong event, at least until January 1993 (see Fig. 6).

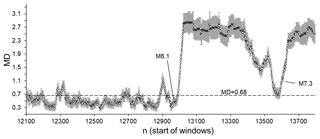
Figure 7 Average MD values calculated for the period from 14 May 1990 (12100) to 28 June 1992 (13797) in which two strong earthquakes occurred: M 6.1 (23 April 1992) and M 7.3 (28 June 1992). MD values are calculated by comparing ICT(i), ICD(i), and ICE(i) sequences from the original SC catalogue and from the set of randomised catalogues. The dotted line corresponds to a significant difference between windows at p=0.01. MD values are calculated for 50-data windows shifted by one data step.

The next period selected for detailed analysis was from 24 August 1997 (the window started from event 20760 in the SC catalogue) to 16 October 1999 (the window started from event 21160 in the SC catalogue). Two large events occurred in this period: a moderate M 5.23 earthquake (6 March 1998) and a strong M 7.1 earthquake (16 October 1999). Here, we note the obvious fact that there is no use trying to find the magnitude range that may occur in windows where seismicity behaves in a random-like way. Indeed, our results show (see Figs. 5, 6, and 7) that earthquakes of any size may occur in any window, both those in which the seismic process is closer to regular behaviour and where it is more random. Hence, we cannot speak about a magnitude threshold or about a range of magnitudes in the sense of their immediate influence on changes in the extent of the regularity of seismic process. On the other hand, our results show that during periods of mostly small earthquake generation, prior to the occurrence of a strong earthquake, the seismic process in the majority of windows is indistinguishable from randomness. Thus, as assessed based on simultaneous variations in ICT(i), ICD(i), and ICE(i), the seismic process of relatively small earthquakes' generation prior to strong earthquakes can be regarded as being random-like.

The results shown in Fig. 8 are mostly similar to those in Fig. 7. Strong and relatively strong (for this selected short period) earthquakes are preceded by a significant number of windows in which the seismic process in the original catalogue is indistinguishable from that observed for randomised catalogues. In contrast, in all 50-data windows following strong (or relatively strong) earthquakes, we can observe a statistically significant difference. A multivariate comparison of these windows based on the variation in ICT(i), ICD(i), and ICE(i) demonstrates that in these windows, the original seismic process is significantly different from the processes taking place in the randomised catalogues (see Figs. 7 and 8).

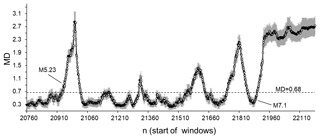
Figure 8 Average MD values calculated for the period from 24 August 1997 (20760) to 16 October 1999 (21160) in which two strong earthquakes occurred: M 5.23 (6 March 1998) and M 7.1 (16 October 1999). The MDs are calculated by comparing ICT(i), ICD(i), and ICE(i) sequences from the original SC catalogue and from the set of randomised catalogues. The dotted line corresponds to a significant difference between the windows at p=0.01. MD values are calculated for 50-data windows shifted by one data step.

Separate consideration of the period of the strong M 7.2 earthquake occurrence leads to a similar conclusion. From Fig. 9, we can again observe that prior to strong earthquakes, the seismic process looks mostly random, and that the extent of order strongly increases after these events.

As expected, the behaviour of the seismic process prior to and following all of the strong events considered here is similar. The only difference is the length of the period during which the post-earthquake seismic process remains significantly regular compared to the randomised catalogues. For strong earthquakes, this period is clearly longer (see Fig. 6). This appears to be connected with the generation of a series of aftershocks, in which the spatial, temporal, and energetic features are causally related to the mainshock. This is in agreement with the well-known productivity law that states that the larger the magnitude of the mainshock, the larger the total number of aftershocks (Helmstetter, 2003; Baiesi and Paczuski, 2004; Godano and Tramelli, 2016). Here, we emphasise that the question of the temporal length of the aftershock sequence following a strong earthquake is still not understood, as it is related to the timescale of background seismic activity (Godano and Tramelli, 2016).

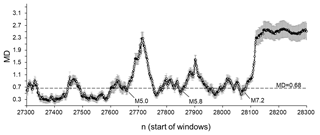
Figure 9 Average MD values calculated for the period from 30 October 2008 (27300) to 5 April 2010 (28300) in which three moderate and strong earthquakes occurred: M 5.0 (1 October 2009), M 5.8 (30 December 2009), and M 7.2 (4 April 2010). MDs are calculated by comparing ICT(i), ICD(i), and ICE(i) sequences from the original SC catalogue and from the set of randomised catalogues. The dotted line corresponds to a significant difference between windows at p=0.01. MD values are calculated for 50-data windows shifted by one data step.

From Figs. 7 to 9, we can see that the extent of order in the seismic process (as assessed based on the temporal, spatial, and energetic distributions of earthquakes) may change not only in the periods prior to and following strong (M 7.3, M 7.2, and M 7.1) earthquakes, but also prior to and following other events that are not as strong, or even moderate. For example, as can be seen from Fig. 8, the M 4.93 (14 May 1999, in window 21570) and M 4.71 (24 August 1999, in window 21776) earthquakes are preceded by windows in which the seismic process mostly appears random, and are followed by windows in which the extent of order of the seismic process is markedly increased. The only difference is that for strong earthquakes, the number of windows in which the extent of order increases is much larger than for moderate ones. A similar conclusion can be drawn from Figs. 7 and 9. Thus, the most important conclusion is that prior to almost all strong earthquakes, in periods which can be regarded as relatively seismically calm, the original seismic process is indistinguishable from a random process, as assessed based on the MD values calculated for windows of 50-data sequences of ICT(i), ICD(i), and ICE(i) characteristics. In this sense, the end part of the catalogue analysed in our work (where we found a long sequence of windows (see Figs. 5 and 6) in which the seismic process is indistinguishable from randomness, observed in a period when seismic activity could be regarded as relatively calm) is particularly interesting regarding the future activity of the fault.¹

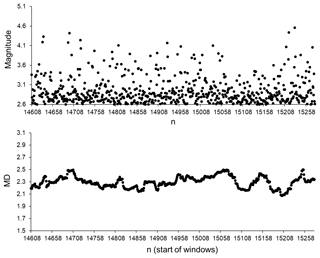
Figure 10 Magnitudes and MD values calculated for part of the SC catalogue after M 7.3 (28 June 1992, sequential number in SC catalogue 13648) from 1 July 1992 (sequential number in SC catalogue 14608) to 5 July 1992 (sequential number in SC catalogue 15280). Average MD values are calculated for 50-data windows shifted by one data step; 90 % of the earthquakes in this period occurred within a distance of 0.5–70 km from the epicentre of M 7.3.

Since the above results suggest that, prior to strong earthquakes, a comparatively calm seismic process of relatively small (with M<4.6, Hough and Jones, 1997) earthquake generation is random-like, it was necessary to carry out an additional analysis of the behaviour of these small events in the case where they occur in windows after strong events. To achieve this, we selected periods of relatively low seismic activity, involving events with magnitudes M≤4.6. We considered 2- to 5-day periods of aftershock activity that was weaker than M 4.6 (soon after strong earthquakes). Figures 10 to 12 show the results of analysis for three such periods following strong earthquakes of M 7.3, M 7.1, and M 7.2. As can be seen from these figures, there are no windows in which the original seismic process, according to MD values calculated for windows of ICT(i), ICD(i), and ICE(i) characteristics, can be regarded as random-like. In all of the windows analysed, when a clear aftershock activity follows immediately after a strong earthquake, the seismic process is significantly different from a random process. In other words, in the original catalogue, the seismic process after strong events in periods of relatively small (M≤4.6) earthquake generation is significantly more regular than the randomised catalogues. It can also be noted that a similar situation was seen for sequences of small events occurring after other strong earthquakes in the analysed catalogue. This offers further evidence that in periods of aftershock activity, the original seismic process is strongly different from that observed for the randomised catalogues in which we distorted the spatial, temporal, and energetic distribution features.

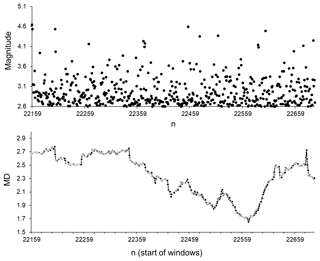
Figure 11 Magnitudes and MD values calculated for part of the SC catalogue after M 7.1 (16 October 1999, sequential number in SC catalogue 21937) from 16 October 1999 (sequential number in SC catalogue 22159) to 21 October 1999 (sequential number in SC catalogue 22697). Average MD values are calculated for 50-data windows shifted by one data step; 92 % of earthquakes in this period occurred within a distance of 1.2–60 km from the epicentre of M 7.1.

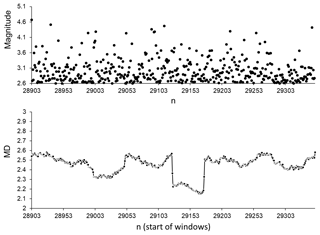
Figure 12 Magnitudes and MD values calculated for part of the SC catalogue after M 7.2 (4 April 2010, sequential number in SC catalogue 28129) from 6 April 2010 (sequential number in SC catalogue 28903) to 8 April 2010 (sequential number in SC catalogue 29350). Average MD values were calculated for 50-data windows shifted by one data step; 99 % of the earthquakes in this period occurred within a distance of 0.7–60 km from the epicentre of M 7.2.

We then carried out a similar analysis for the sequences of relatively small earthquakes that occurred in periods when no strong earthquakes were registered. These small earthquakes apparently cannot be regarded as aftershocks of strong events. In Fig. 13, we present the results of an analysis of an almost 2-year period of small earthquake activity. This period began 5 months later, after the M 5.12 earthquake (1 October 1982, sequential number in SC catalogue 4591) which was the closest event exceeding the selected M 4.6 threshold. According to the proposed view of the time distribution of aftershocks, it looks very unlikely that the M 5.12 earthquake could invoke aftershock activity which lasted 2 years. Thus, in agreement with our above findings, we can conclude that for the selected period, the seismic process in the original catalogue is indistinguishable from the set of catalogues that were randomised using a shuffling procedure in 60 % of the 50-data windows considered.

Figure 14 presents the results for the next part of the catalogue, which contained relatively small earthquakes in the observation period, which was far from the occurrence of strong events. A moderately strong earthquake of M 5.43 (7 July 2010, sequential number in SC catalogue 31011) occurred 9 months prior to the start of this 10-month long period of small earthquake activity, which lasted from 7 April 2011 (sequential number in SC catalogue 31823) to 14 February 2012 (sequential number in SC catalogue 32240). In this case, we observe that in 75 % of the 50-data windows analysed, the seismic process in the original catalogue is indistinguishable from the set of randomised catalogues.

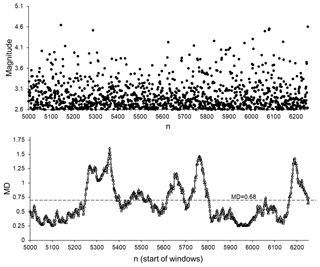
Figure 13 Magnitudes and MD values calculated for the non-aftershock part of the SC catalogue from 7 March 1983 (sequential number in SC catalogue 5000) to 5 February 1985 (sequential number in SC catalogue 6253). Average MD values are calculated for 50-data windows shifted by one data step.

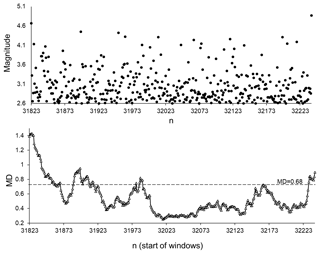
Figure 14 Magnitudes and MD values calculated for the non-aftershock part of the SC catalogue from 7 April 2011 (sequential number in SC catalogue 31823) to 14 February 2012 (sequential number in SC catalogue 32240). Average MD values are calculated for 50-data windows shifted by one data step.

In Fig. 15, we present the results for the third part of the catalogue, which was selected to contain relatively small earthquakes, M≤4.6, in a period far from strong events (the closest such earthquake of M 7.1 occurred more than 5 years earlier, on 16 October 1999, sequential number in SC catalogue 21937). Two moderately strong M 5.7 earthquakes (8 December 2001 and 22 February 2002 with sequential numbers in SC catalogue 24491 and 24640) also occurred a long time before the selected period, which lasted from 24 May 2006 to 5 August 2007. Within this period of generation of small earthquakes, 84 % of the 50-data windows indicated that the seismic activity in the original catalogue is indistinguishable from the set of randomised catalogues.

Figure 15 Magnitudes and MD values calculated for the non-aftershock part of the SC catalogue from 24 May 2006 (sequential number in SC catalogue 26259) to 5 August 2007 (sequential number in SC catalogue 26717). Average MD values are calculated for 50-data windows shifted by one data step.

6 Testing the stability of the results with respect to the minimum magnitude

As can be seen from our results, as assessed based on the ICT(i), ICD(i), and ICE(i) characteristics, the seismic process of generation of relatively small earthquakes often (although not always) appears random and strongly depends on the space and time location of these small earthquake sequences. It can be assumed that if the observed indistinguishability from randomness really is connected with the features of the seismic process in periods preceding strong events, then this indistinguishability should also be retained for higher values of the completeness magnitude threshold. To test this assumption, we carried out the same analysis for the SC earthquake catalogue with representative thresholds of M 3.6 and M 4.6. A further increase in the threshold to M 5.6 was not feasible, since only 29 earthquakes with magnitudes larger than M 5.6 occurred in the SC catalogue during the period considered in this research.

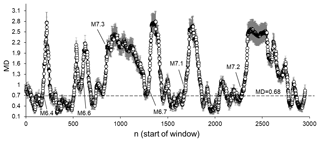
Figure 16 Average MD values calculated by comparing ICT(i), ICD(i), and ICE(i) sequences from the original SC catalogue and from the set of randomised catalogues (completeness threshold M 3.6). The dotted line corresponds to a significant difference between windows at p=0.01. MD values are calculated for 50-data windows shifted by one data step.

In Fig. 16, we give results for a completeness magnitude threshold of M 3.6. We can see that the situation for windows in which the seismicity is indistinguishable from randomness is almost exactly the same as in Fig. 6, for a completeness magnitude threshold of M 2.6. Specifically, in 33 % of all 50-data windows, the seismic process looks similar to the random process in catalogues where the dynamical structure of the original seismic process was intentionally distorted. These random-like windows in the original catalogue preceded strong events.

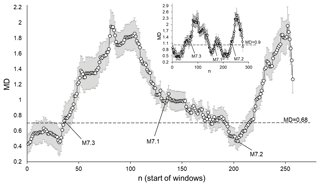
Figure 17 Average MD values calculated by comparing ICT(i), ICD(i), and ICE(i) sequences from the original SC catalogue and from the set of randomised catalogues (completeness threshold M 4.6). The dotted line corresponds to a significant difference between windows at p=0.01. MD values are calculated for 50-data windows shifted by one data step. The inset shows results calculated for 30-data windows shifted by one data step.

As can be seen from Fig. 17, in the case of a higher threshold of M 4.6 prior to two strong events, M 7.3 and M 7.2, we observe windows (of 50 data steps) in which the seismic process assessed based on the ICT(i), ICD(i), and ICE(i) characteristics is indistinguishable from the randomised catalogues. In total, 21 % of the 50-data windows had calculated MDs lower than the significance threshold value (0.68). Conversely, at a high representative threshold (M 4.6), unlike in the above cases, prior to a strong M 7.1 earthquake, we do not observe 50-data windows in which the seismic process could be regarded as random.

This behaviour is apparently caused by the small number of events above the M 4.6 threshold (below which, as explained above, we regarded earthquakes as small, Hough and Jones, 1997) in the catalogue, and by the selected length of the window (50 data steps) for the short data sequence. In the case of 30 data windows shifted by one data step, we see that prior to the M 7.1 earthquake there are also windows that are indistinguishable from the random catalogues (see inset in Fig. 17). The proportion of windows showing random behaviour of the seismic process is 37 %. Summarising the results in Fig. 17, we can say that shorter windows (apparently in the range 30–50 data steps) seem to be preferable for an analysis such as this. A more important observation from the results for the high threshold is that the random-like character of the seismic process observed in windows prior to strong events apparently is not (or is not always) connected only with small earthquakes. It seems that long-range correlation features in the seismic process should not be regarded as being directly related to the sizes of events.

7 Conclusions

We have investigated the variability in the regularity of the seismic process, based on its spatial, temporal, and energetic characteristics. For this purpose, we used an SC earthquake catalogue over the period 1975 to 2017. Our method of analysis was a combination of multivariate Mahalanobis distance calculation and surrogate data testing. We carried out a multivariate assessment of changes in the regularity of the seismic process, based on increments of cumulative times, increments of cumulative distances, and increments of cumulative seismic energies calculated from the SC earthquake catalogue.

In order to assess the ability of the multivariate approach used here to discriminate between different conditions of dynamical systems, we used two 3-D models in which the dynamical features were changed from a more regular form to more randomised conditions by adding a certain degree of noise.

It was shown that in about a third of the analysed 50-data windows, the original seismic process is indistinguishable from a random process by the features of its temporal, spatial, and energetic variability. Prior to the occurrence of strong earthquakes, in periods in which there are events with relatively small magnitudes (<M 4.6), the percentage of windows in which the seismic process is indistinguishable from a random process increases to 60 %–80 %. At the same time, during periods of aftershock activity, the process of small earthquake generation becomes more regular in all of the windows considered and thus is strongly differentiated from the randomised catalogues.

Based on the results of our analysis, we conclude that the seismic process cannot in general be regarded either as completely random or as completely regular (deterministic). Instead, we can say that the dynamics of the seismic process undergoes strong time-dependent changes. In other words, the regularity of the seismic process, as assessed based on the temporal, spatial, and energetic distributions, changes over time.

It was also shown that in some periods, the seismic process appears to be closer to randomness, while in other cases it becomes closer to regular behaviour. More specifically, in periods of relatively low earthquake generation activity (i.e. with smaller energy release), the seismic process looks more random, while in periods of occurrence of strong events, followed by a series of aftershocks, it shows significant deviation from randomness (i.e. the extent of regularity essentially increases). The period for which this deviation from random behaviour lasts depends on the amount of seismic energy released by the strong earthquake. The results obtained here from a multivariable assessment of the dynamical features of the seismic process are in accordance with our previous findings on the dynamical changes in the temporal distribution of earthquakes (Matcharashvili et al., 2018).

It should be underlined that the occurrence in July 2019 (during the editorial process of our manuscript in NPG) of two strong earthquakes, M 6.4 and M 7.1, in the considered catalogue area additionally convinced us that random-like behaviour of seismic processes may indeed be regarded as one of the possible precursory markers of strong earthquakes.