Data assimilation as a learning tool to infer ordinary differential equation representations of dynamical models

Recent progress in machine learning has shown how to forecast and, to some extent, learn the dynamics of a model from its output, resorting in particular to neural networks and deep learning techniques. We will show how the same goal can be directly achieved using data assimilation techniques without leveraging on machine learning software libraries, with a view to high-dimensional models. The dynamics of a model are learned from its observation and an ordinary differential equation (ODE) representation of this model is inferred using a recursive nonlinear regression. Because the method is embedded in a Bayesian data assimilation framework, it can learn from partial and noisy observations of a state trajectory of the physical model. Moreover, a space-wise local representation of the ODE system is introduced and is key to coping with high-dimensional models.

It has recently been suggested that neural network architectures could be interpreted as dynamical systems. Reciprocally, we show that our ODE representations are reminiscent of deep learning architectures. Furthermore, numerical analysis considerations of stability shed light on the assets and limitations of the method.

The method is illustrated on several chaotic discrete and continuous models of various dimensions, with or without noisy observations, with the goal of identifying or improving the model dynamics, building a surrogate or reduced model, or producing forecasts solely from observations of the physical model.

1 Introduction

1.1 Data assimilation and model error

Data assimilation aims at estimating the state of a physical system from its observation and a numerical dynamical model for it. It has been successfully applied to numerical weather and ocean prediction, where it often consisted in estimating the initial conditions for the state trajectory of chaotic geofluids (Kalnay, 2002; Asch et al., 2016; Carrassi et al., 2018). This objective is impeded by the deficiencies of the numerical model (discretrisation, approximate physical schemes, unresolved scales, and their uncertain parametrisations, e.g. Harlim, 2017) and the difficulty in matching numerical representations of the system with the observations (representation error, Janjić et al., 2018). As a result, the quality of numerical weather predictions based on a methodologically sound data assimilation method crucially depends on both the sensitivity to the initial condition due to the chaotic unstable dynamics and on model error (Magnusson and Källén, 2013).

Model errors can take many forms, and accounting for them depends on the chosen data assimilation scheme. A first class of solutions relies on parametrising model error by, for instance, transforming the problem into a physical parameter estimation problem (e.g. Bocquet, 2012; Aster et al., 2013). Other solutions are based on a weakly parametrised form of model error, for instance when it is assumed to be additive noise. Such techniques have been developed for variational data assimilation (e.g. Trémolet, 2006; Carrassi and Vannitsem, 2010), for ensemble Kalman filters and smoothers (e.g. Ruiz et al., 2013; Raanes et al., 2015), and for ensemble-variational assimilation (Amezcua et al., 2017; Sakov et al., 2018). In the weakly parametrised form, these methods should be completed by an estimation of the model error statistics (e.g. Pulido et al., 2018; Tandeo et al., 2019). Moreover, a model error's impact can be mitigated, and this is often the case in applications, by multiplicative and additive inflation (e.g. Whitaker and Hamill, 2012; Grudzien et al., 2018; Raanes et al., 2019) and by physically driven stochastic perturbations of model simulations in ensemble approaches (e.g. Buizza et al., 1999) or by stochastic subgrid parametrisations (e.g. Resseguier et al., 2017). This account is very far from exhaustive as this is a vast, multiform, and very active subject of research.

These approaches essentially seek to correct, calibrate, or improve an existing model using observations. Hence, they all primarily make use of data assimilation techniques.

1.2 Data-driven forecast of a physical system

An alternative is to renounce physically based numerical models of the phenomenon of interest and instead to only use observations of that system. Given the huge required datasets, this may seem a far-reaching goal for operational weather and ocean forecasting systems, but recent progress in data-driven methods and convincing applications to geophysical problems of small to intermediate complexity are strong incentives to investigate this bolder approach. Eventually, the perspective of putting numerical models away has a strong practical appeal, even though such a perspective may generate intense debates.

For instance, forecasting of a physical system can be done by looking up past situations and patterns using the techniques of analogues, which can be combined with present observations using data assimilation (Lguensat et al., 2017), or it can rely on a representation of the physical system based on diffusion maps that look for a spectral representation of the dataset (see chapter 6 of Harlim, 2018). An original data-driven stochastic modelling approach has been developed by Kondrashov et al. (2015). The method, recently extended to deal with multi-scale datasets (Kondrashov and Chrekroun, 2017), has been applied to successfully estimate reduced models of geophysical phenomena (see e.g. Kondrashov et al., 2018, and references therein). A fourth route relies on neural networks and deep learning to represent the hidden model and make forecasts from this representation. Examples of such an approach applied to the forecasting of low-order chaotic geophysical models are Park and Zhu (1994), who used a bilinear recurrent neural network and applied it to the three-variable Lorenz model (Lorenz, 1963, hereafter L63), Pathak et al. (2017, 2018), who use reservoir network techniques on the L63 model and on the Kuramoto–Sivashinski model (Kuramoto and Tsuzuki, 1976; Sivashinsky, 1977, hereafter KS), and Dueben and Bauer (2018), who use a neural network on a low-order Lorenz three-scale model and on coarse two-dimensional geopotential height maps at 500 hPa. The last three contributions have to resort to local reservoir networks or convolutional layers, respectively, to cope with the dimensionality of the models. However, all these representations are not mechanistic and the neural network becomes a surrogate for the hidden model. This marks a key distinction with respect to our approach where the dynamics to be determined are explicitly formulated, as will be clarified later.

1.3 Learning the dynamics of a model from its output

Data-driven techniques that seek to represent the model in a more explicit manner, and therefore with a greater interpretability, may use specific classes of nonlinear regression as advocated by Paduart et al. (2010) and Brunton et al. (2016). With a view to forecasting dynamical systems, it is possible to design neural networks in order to reflect the iterative form of a Runge–Kutta (RK) integration scheme. Wang and Lin (1998) proposed and achieved such a goal using classical activation functions, which may however blur the interpretation of the underlying dynamics. Fablet et al. (2018) went further and used a bilinear residual neural network structured so as to mimic a fourth-order RK scheme (RK4) and noise-free data. Using the Keras tool with the TensorFlow backend, their approach proved to be a very effective tool for the L63 model and to a lesser extent for the 40-variable Lorenz model (Lorenz and Emanuel, 1998, hereafter L96). In particular, they retrieved the parameters of the L63 equations to a high precision. Long et al. (2018) sought the operators of the partial differential equations (PDEs) of a physical system by identifying differentiations with convolution operators of a feed-forward neural network. They successfully applied their method to advection–diffusion problems. As opposed to our proposal, described hereafter, none of the aforementioned techniques is embedded in a Bayesian framework, making them less suitable for working with noisy and partial data.

1.4 Goal and outline

From this point on, the physical system under scrutiny will be called the reference model. It will be assumed to be known only from observations. We follow a data-driven approach inspired by the works of Paduart et al. (2010) and Fablet et al. (2018) in the sense that we will consider an observed physical reference model, which might be generated by a hidden mathematical model or process. This work is focused on either one or a combination of the following goals: (i) to build a surrogate model for the dynamics, (ii) to produce forecasts that emulate those of the reference model, and (iii) to identify the underlying dynamics of the reference model given by a mathematical model. The reference model could be totally unknown or only partially specified. To achieve these goals, we introduce a surrogate model defined by a set of ordinary differential equations (ODEs):

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}\mathit{x}}{\mathrm{d}t}}=\mathit{\varphi }\left(\mathit{x}\right),\end{array}$$

where $\mathit{x}\in {\mathbb{R}}^{N_x}$ is the state vector and x↦ϕ(x) is a vector field that we shall call the flow rate. For the sake of simplicity, the dynamics in this study are supposed to be autonomous, i.e. do not explicitly depend on time. Our technique seeks a fit ϕ given observations of the reference model. This is a rather general representation since, for instance, PDEs can be discretised into ODEs. We will restrict ourselves to the case where ϕ is at most quadratic in ${\left\{x_n\right\}}_{\mathrm{0}\le n<N_x}$. The numerical integration of Eq. (1) could be based on any RK scheme, but should additionally rely on the composition of such integration steps. As a result, quite general resolvents of Eq. (1) can be built (the resolvent is the model, i.e. the flow rate, integrated in time over a finite time interval).

Importantly, we will not require any machine learning software tool since the adjoint of the model resolvent can be derived without a lot of effort. As opposed to the contributions mentioned in the previous subsections, we embed the technique in a data assimilation framework. From a data assimilation standpoint, the technique can be seen as meant to deal with model error (with or without some prior on the model) and it naturally accommodates partial and noisy observations. Moreover, we will build representations of the dynamics that are either invariant by spatial translation (homogeneous) and/or local (i.e. the flow rate of a variable x_n only depends on neighbouring variables whose perimeter is defined by a stencil). These properties make our technique scalable and thus potentially applicable to high-dimensional systems.

In Sect. 2, we present model identification as a Bayesian data assimilation problem. We first choose an ODE representation of the dynamics, introduce a nonlinear regressor basis, and define the integration schemes we will work with. We describe the local and homogeneous representations as physically based simplifications of the most general case, and we derive the gradient of the problem's cost function based on these representations. We then introduce the Bayesian problem and the resulting cost function used for joint supervised learning of the optimal representation and estimation of the state trajectory. The latter is the standard goal of data assimilation, while the former is that of machine learning. Our approach blends them together using the formalism of data assimilation.

In Sect. 3, we discuss several theoretical issues: the prior of the model, the convergence of the training step, the connection with numerical analysis of integration schemes, the connection with deep learning architectures, and, finally, the pros and cons of our approach.

In Sect. 4, we illustrate the method with several low-order chaotic models (L63, L96, KS, and a two-scale Lorenz model) of various sizes, from a perfectly identifiable model, i.e. where the model used to generate the dataset can be retrieved exactly, to a reduced-order model where the model used to generate the dataset cannot be retrieved exactly, using full or partial, noiseless, or noisy observations. Conclusions are given in Sect. 5.

2 Model identification as a data assimilation problem

2.1 Ordinary differential equation representation

Our surrogate model is chosen to be represented by an ODE system as described by Eq. (1). We additionally assume that the flow rate can be written as

$$\begin{array}{}\text{(2)}& {\mathit{\varphi }}_{\mathbf{A}}\left(\mathit{x}\right)=\mathbf{A}\mathit{r}\left(\mathit{x}\right),\end{array}$$

where $\mathbf{A}\in {\mathbb{R}}^{N_x\times N_p}$ is a matrix of real coefficients to be estimated and $\mathit{r}:{\mathbb{R}}^{N_x}\mapsto {\mathbb{R}}^{N_p}$ is a map that defines regressor functions of x. ${\mathbb{R}}^{N_p}$ is the latent space of the regressors in which the flow rate is linear.

In the absence of any peculiar symmetry, we choose this map to list all the monomials up to second order built on x, i.e. the constant, linear, and bilinear monomials. Let us call $\mathcal{D}=\left\{\mathrm{0},\mathrm{1},\mathrm{\dots },N_x-\mathrm{1}\right\}$ the set of all variable indices and 𝒫 the set of all pairs of variable indices. We introduce the augmented state vector

$$\begin{array}{}\text{(3)}& \stackrel{\mathrm{̃}}{\mathit{x}}=\left[\begin{array}{c}\mathit{x}\\ \mathrm{1}\end{array}\right]\in {\mathbb{R}}^{N_x+\mathrm{1}},\end{array}$$

extend 𝒟 to $\stackrel{\mathrm{̃}}{\mathcal{D}}=\mathcal{D}\cup \left\{N_x\right\}$, and define $\stackrel{\mathrm{̃}}{\mathcal{P}}$ as the distinct pairs of variable indices in $\stackrel{\mathrm{̃}}{\mathcal{D}}$.

As a result, the regressors are compactly defined by

$$\begin{array}{}\text{(4)}& \mathit{r}\left(\mathit{x}\right)=\left[{\left\{{\stackrel{\mathrm{̃}}{x}}_n{\stackrel{\mathrm{̃}}{x}}_m\right\}}_{(n,m)\in \stackrel{\mathrm{̃}}{\mathcal{P}}}\right],\end{array}$$

where the scalars in the bracket are the entries of the vector r(x). We count

$$\begin{array}{}\text{(5)}& N_p=\left(\genfrac{}{}{0ex}{}{N_x+\mathrm{1}}{\mathrm{2}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(N_x+\mathrm{1})(N_x+\mathrm{2})\end{array}$$

regressors, i.e. the cardinal of $\stackrel{\mathrm{̃}}{\mathcal{P}}$. For instance, a model with three variables, x₀,x₁, and x₂, such as L63, has 10 such regressors:

$$\begin{array}{}\text{(6)}& \left[\mathrm{1},x_{\mathrm{0}},x_{\mathrm{1}},x_{\mathrm{2}},x_{\mathrm{0}}^{\mathrm{2}},x_{\mathrm{0}}{x}_{\mathrm{1}},x_{\mathrm{0}}{x}_{\mathrm{2}},x_{\mathrm{1}}^{\mathrm{2}},x_{\mathrm{1}}{x}_{\mathrm{2}},x_{\mathrm{2}}^{\mathrm{2}}\right].\end{array}$$

Higher-order regressors, as well as regressors of different functional forms, could be included as in Brunton et al. (2016). However, it is important to keep in mind that we do not seek an expansion of the resolvent of the reference model, but of the flow rate ϕ_A. As a consequence, higher-order products of the state variables are anyhow generated by the integration schemes and their composition. It is worth mentioning that nonlinear regressions are not widespread in geophysical data assimilation. We are nonetheless aware of at least one noticeable exception that extends traditional Gaussian-based methods (Hodyss, 2011, 2012).

2.2 Local and homogeneous representations

At least two useful simplifications for the ODEs could be exploited if the state x is assumed to be the discretisation of a spatial field.

2.2.1 Locality

First, we use a locality assumption based on the physical locality of the system: all multivariate monomials in the ODEs have variables x_n that belong to a stencil, i.e. a local arrangement of grid points around a given node. This can significantly reduce the number of bilinear monomials in r(x). We assume that s_n is the stencil around node n, the pattern being the same for all nodes except the last one. For the node N_x corresponding to the extra variable ${\stackrel{\mathrm{̃}}{x}}_{N_x}=\mathrm{1}$, we assume that its stencil consists of all the N_x+1 nodes. We then define ${\stackrel{\mathrm{̃}}{\mathcal{P}}}_s\subset \stackrel{\mathrm{̃}}{\mathcal{P}}$ as the sub-set of all pairs (n,m) of variables for which m∈s_n. The set of required monomials can therefore be reduced to

$$\begin{array}{}\text{(7)}& \mathit{r}\left(\mathit{x}\right)=\left[{\left\{{\stackrel{\mathrm{̃}}{x}}_n{\stackrel{\mathrm{̃}}{x}}_m\right\}}_{(n,m)\in {\stackrel{\mathrm{̃}}{\mathcal{P}}}_s}\right].\end{array}$$

Under these conditions, A becomes sparse. Indeed, for each node n, we assume that ${\dot{x}}_n$, the time derivative of x_n, is impacted only by linear terms x_m such that m∈s_n and quadratic terms x_mx_l such that m∈s_n, l∈s_n, and m∈s_l. However, to keep a dense matrix, we choose to compactly redefine and shrink A by eliminating all a priori zero entries due to the locality assumption. The number of columns of A is then significantly reduced from N_p to N_a. As a consequence of this redefinition of A, the matrix multiplication in between A and r(x) must be changed accordingly. Nonetheless, the operation that assigns coefficients in A to the monomials in r(x) remains linear, and we write it as

$$\begin{array}{}\text{(8)}& {\mathit{\varphi }}_{\mathbf{A}}\left(\mathit{x}\right)=\mathbf{A}\cdot \mathit{r}\left(\mathit{x}\right).\end{array}$$

Let us take the example of a one-dimensional extended space as those used in Sect. 4. The domain is supposed to be periodic (circle) and the nodes are indexed by $\mathrm{0}\le n<N_x$. Recall that the node of index N_x is associated with the extra {1}. For $\mathrm{0}\le n<N_x$, the stencil s_n is defined as the set of 2L+1 nodes of index $n-L,n-L+\mathrm{1},\mathrm{\dots }n+L-\mathrm{1},n+L$, plus the extra node of index N_x. The stencil $s_{N_x}$ consists of all the nodes, i.e. 𝒟. We assume $\mathrm{2}L+\mathrm{1}\le N_x$. In that case r(x) as defined by Eq. (7) has $N_p=\mathrm{1}+N_x(\mathrm{2}+L)$ monomials. For instance, there are 161 such regressors for a 40-variable model defined on a circular domain, such as L96, with L=2:

$$\begin{array}{}\text{(9)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }\left[\mathrm{1},\right.\\ {\displaystyle }& {\displaystyle }{x}_{\mathrm{0}},x_{\mathrm{1}},\mathrm{\dots },x_{\mathrm{39}},\\ {\displaystyle }& {\displaystyle }{x}_{\mathrm{0}}^{\mathrm{2}},x_{\mathrm{0}}{x}_{\mathrm{1}},x_{\mathrm{0}}{x}_{\mathrm{2}},\\ {\displaystyle }& {\displaystyle }{x}_{\mathrm{1}}^{\mathrm{2}},x_{\mathrm{1}}{x}_{\mathrm{2}},x_{\mathrm{1}}{x}_{\mathrm{3}},\\ {\displaystyle }& {\displaystyle }\mathrm{⋮}\\ {\displaystyle }& {\displaystyle }\left.x_{\mathrm{39}}^{\mathrm{2}},x_{\mathrm{39}}{x}_{\mathrm{0}},x_{\mathrm{39}}{x}_{\mathrm{1}}\right].\end{array}\end{array}$$

The row [A]_n of the dense A contains the following coefficients for each $\mathrm{0}\le n<N_x$. First there are 2L+2 regressors built with {1} (the constant and linear regressors). Second, we consider the square monomials $x_m^{\mathrm{2}}$ with m∈s_n, i.e. ${\left\{x_m^{\mathrm{2}}\right\}}_{n-L\le m\le n+L}$ whose number is 2L+1. Then we consider those separated by one space step, ${\left\{x_m{x}_{m+\mathrm{1}}\right\}}_{n-L\le m\le n+L-\mathrm{1}}$ whose number is 2L, followed by those separated by two space steps whose number is 2L−1, and so on until a separation of L is reached. Quadratic monomials of greater separation are discarded since they do not belong to a common stencil as per the above definition reflecting the locality assumption. Hence there is a total of $N_{\mathrm{a}}={\sum }_{l=L+\mathrm{1}}^{\mathrm{2}L+\mathrm{2}}l=\frac{\mathrm{3}}{\mathrm{2}}(L+\mathrm{1})(L+\mathrm{2})$ coefficients per grid cell.

In Appendix A, we show in the one-dimensional space case how to compute the reduced form of the product between A and r(x), assuming locality. This type of technical parametrisation is required for a parsimonious representation of the control variables, i.e. the coefficients of A, and is key for a successful implementation with high-dimensional models.

Note that this locality assumption is hardly restrictive. Indeed, owing to the absence of long-range instantaneous interactions (which are precluded in geophysical fluids), farther distance correlations between state variables can be generated by small stencils in the definition of ϕ_A through time integrations. This would not prevent potential specific long-distance dependencies (such as teleconnections).

2.2.2 Homogeneity

Furthermore, a symmetry hypothesis could optionally be used by assuming translational invariance of the ODEs, called homogeneity in the following. Because our control parameters, i.e. the coefficients of A, parametrise the flow rate, the symmetry simply translates into the rows [A]_n of the dense A being the same for all n. Hence A simply becomes a vector in ${\mathbb{R}}^{N_{\mathrm{a}}}$.

Let us enumerate its coefficients in the case of the L96 model with L=2 and assuming both locality and homogeneity. The coefficients are partitioned into A⁽⁰⁾ for the bias, $A_l^{\left(\mathrm{1}\right)}$ for the linear sector, and $A_{l,m}^{\left(\mathrm{2}\right)}$ for the bilinear sector. In the linear sector, $l=-\mathrm{2},\mathrm{\dots },\mathrm{2}$ is the relative position with respect to the current grid point. In the bilinear sector, l,m are the relative positions with respect to the current grid point of the two variables in the product. Proceeding in the same way we counted them, the N_a=18 coefficients of A are

$$\begin{array}{}\text{(10)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }\left[A^{\left(\mathrm{0}\right)},\right.\\ {\displaystyle }& {\displaystyle }{A}_{-\mathrm{2}}^{\left(\mathrm{1}\right)},A_{-\mathrm{1}}^{\left(\mathrm{1}\right)},A_{\mathrm{0}}^{\left(\mathrm{1}\right)},A_{\mathrm{1}}^{\left(\mathrm{1}\right)},A_{\mathrm{2}}^{\left(\mathrm{1}\right)},\\ {\displaystyle }& {\displaystyle }{A}_{-\mathrm{2},-\mathrm{2}}^{\left(\mathrm{2}\right)},A_{-\mathrm{1},-\mathrm{1}}^{\left(\mathrm{2}\right)},A_{\mathrm{0},\mathrm{0}}^{\left(\mathrm{2}\right)},A_{\mathrm{1},\mathrm{1}}^{\left(\mathrm{2}\right)},A_{\mathrm{2},\mathrm{2}}^{\left(\mathrm{2}\right)},\\ {\displaystyle }& {\displaystyle }{A}_{-\mathrm{2},-\mathrm{1}}^{\left(\mathrm{2}\right)},A_{-\mathrm{1},\mathrm{0}}^{\left(\mathrm{2}\right)},A_{\mathrm{0},\mathrm{1}}^{\left(\mathrm{2}\right)},A_{\mathrm{1},\mathrm{2}}^{\left(\mathrm{2}\right)},\\ {\displaystyle }& {\displaystyle }\left.A_{-\mathrm{2},\mathrm{0}}^{\left(\mathrm{2}\right)},A_{-\mathrm{1},\mathrm{1}}^{\left(\mathrm{2}\right)},A_{\mathrm{0},\mathrm{2}}^{\left(\mathrm{2}\right)},\right].\end{array}\end{array}$$

Note that while both constraints, locality and homogeneity, apply to the ODEs, they do not apply to the states per se. For instance, ODEs for discretised homogeneous two-dimensional turbulence satisfy both constraints and yet generate non-uniform flows.

For realistic geofluids, the forcing fields (solar irradiance, bathymetry, boundary conditions, friction, etc.) are heterogeneous, so that the homogeneity assumption should be dropped. Nonetheless, the fluid dynamics part of the model would remain homogeneous. As a result, a hybrid approach could be enforced.

2.3 Integration scheme and cycling

The reference model will be observed at time steps t_k, indexed by integer $\mathrm{0}\le k\le K$. Hence, we need to be able to express the resolvent of the surrogate model from t_k to t_k+1. We assume that $t_{k+\mathrm{1}}-t_k$ is a multiple of the integration time step of the surrogate model, $t_{k+\mathrm{1}}-t_k=N_{\mathrm{c}}^{k}h$, where h is the integration time step and $N_{\mathrm{c}}^k$ is the number of integrations. The time steps $t_{k+\mathrm{1}}-t_k$ can be uneven, which is reflected in the dependence of $N_{\mathrm{c}}^k$ on k. Hence, the resolvent of the surrogate model from t_k to t_k+1 can be written as

$$\begin{array}{}\text{(11)}& {\mathit{x}}_{k+\mathrm{1}}={\mathbf{F}}_{\mathbf{A}}^k\left({\mathit{x}}_k\right),\text{where}{\mathbf{F}}_{\mathbf{A}}^k\equiv {\mathbf{f}}_{\mathbf{A}}^{N_{\mathrm{c}}^k}\equiv \underset{N_{\mathrm{c}}^k\text{ times}}{\underbrace{{\mathbf{f}}_{\mathbf{A}}\circ \mathrm{\dots }\circ {\mathbf{f}}_{\mathbf{A}}}},\end{array}$$

i.e. the integration of Eq. (1) from t_k to t_k+1 using the representation Eq. (2).

We define intermediate state vectors in between $[t_k,t_{k+\mathrm{1}}]$: x_k,l is the state vector defined at time $t_k+(t_{k+\mathrm{1}}-t_k)l/N_{\mathrm{c}}^k$ for $\mathrm{0}\le l\le N_{\mathrm{c}}^k$, as the result of l compositions of f_A on x_k: ${\mathit{x}}_{k,l}={\mathbf{f}}_{\mathbf{A}}^l\left({\mathit{x}}_k\right)$. Figure 1 is a schematic of the composition of the integration steps, along with the state vectors x_k and x_k,l.

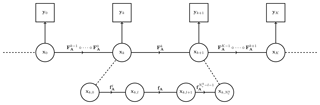
Figure 1 Representation of the data assimilation system as a hidden Markov chain model and of the model resolvents ${\mathbf{F}}_{\mathbf{A}}^k$ and f_A.

The operator f_A is meant to be an explicit numerical integration scheme. In the following, we shall consider an RK scheme applied to $\mathit{x}\equiv {\mathit{x}}_{k,l}$, with N_RK steps. This number of steps coincides with the accuracy of the schemes that we will consider: first order for the Euler scheme, second order for RK2, and fourth order for RK4 ($N_{\mathrm{RK}}=\mathrm{1},\mathrm{2}$, and 4, respectively). Provided the dynamics are autonomous, a general RK scheme reads as

$$\begin{array}{}\text{(12a)}& {\displaystyle }{\mathbf{f}}_{\mathbf{A}}\left(\mathit{x}\right)& {\displaystyle }=\mathit{x}+h\sum _{i=\mathrm{0}}^{N_{\mathrm{RK}}-\mathrm{1}}{\mathit{\beta }}_i{\mathbf{k}}_i,\text{(12b)}& {\displaystyle }{\mathbf{k}}_i& {\displaystyle }={\mathit{\varphi }}_{\mathbf{A}}\left(\mathit{x}+h\sum _{j=\mathrm{0}}^{i-\mathrm{1}}{\mathit{\alpha }}_{i,j}{\mathbf{k}}_j\right),\end{array}$$

where the coefficients β_i and α_i,j entirely specify the scheme and $h=(t_{k+\mathrm{1}}-t_k)/N_{\mathrm{c}}^k$. Note that α_i,j are zero for j≥i, so that Eq. (12b) can be computed iteratively from k₀ to ${\mathbf{k}}_{N_{\mathrm{RK}}-\mathrm{1}}$, followed by the sum Eq. (12a) to get f_A(x).

In the following, h will be absorbed into the definition of A and hence ϕ_A, so that we can take h=1 without loss of generality.

2.4 Bayesian analysis

We consider a sequence of observation vectors ${\mathit{y}}_k\in {\mathbb{R}}^{N_y^k}$ of the physical system at t_k indexed by $\mathrm{0}\le k\le K$. The system state is observed through

$$\begin{array}{}\text{(13)}& {\mathit{y}}_k={\mathbf{H}}_k\left({\mathit{x}}_k\right)+{\mathit{ϵ}}_k,\end{array}$$

where H_k is the observation operator at time t_k. The observation error ϵ_k will be assumed to be Gaussian with zero mean and covariance matrix r_k. It is also assumed to be white in time. The flow rate ϕ_A is given by the approximation Eq. (2), so that the resolvent F_A of the surrogate model should also be considered an approximation of the reference model's resolvent. Hence, we generalise Eq. (11) to

$$\begin{array}{}\text{(14)}& {\mathit{x}}_{k+\mathrm{1}}={\mathbf{F}}_{\mathbf{A}}^k\left({\mathit{x}}_k\right)+{\mathit{\eta }}_k,\end{array}$$

where η_k are unbiased Gaussian errors of covariance matrices Q_k, supposed to be white in time and uncorrelated from the observation errors. Note that, in all generality, the state space of the surrogate model does not have to match that of the reference model. We will nonetheless take them to coincide here merely for simplicity.

With the goal of identifying a model or building a surrogate of the reference one, we are interested in estimating the probability density function (pdf) $p\left(\mathbf{A}\right|{\mathit{y}}_{\mathrm{0}:K})$, where y_0:K stands for all observations in the window [t₀,t_K]. To obtain a tractable expression for this conditional likelihood, we need to marginalise over the state variables x_0:K within the window:

$$\begin{array}{}\text{(15)}& p\left(\mathbf{A}\right|{\mathit{y}}_{\mathrm{0}:K})=\int \mathrm{d}{\mathit{x}}_{\mathrm{0}:K}p(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K}\left|{\mathit{y}}_{\mathrm{0}:K}\right).\end{array}$$

An approximate maximum a posteriori for A could be obtained by using the Laplace approximation of this integral, which would require finding the maximum of

$$\begin{array}{}\text{(16)}& \begin{array}{rl}p(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K}|{\mathit{y}}_{\mathrm{0}:K})& ={\displaystyle \frac{p(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K},{\mathit{y}}_{\mathrm{0}:K})}{p\left({\mathit{y}}_{\mathrm{0}:K}\right)}}\\ & ={\displaystyle \frac{p({\mathit{x}}_{\mathrm{0}:K},{\mathit{y}}_{\mathrm{0}:K}|\mathbf{A}\left)p\right(\mathbf{A})}{p\left({\mathit{y}}_{\mathrm{0}:K}\right)}}\\ & ={\displaystyle \frac{p\left({\mathit{y}}_{\mathrm{0}:K}\right|{\mathit{x}}_{\mathrm{0}:K},\mathbf{A}\left)p\right({\mathit{x}}_{\mathrm{0}:K}\left|\mathbf{A}\right)p\left(\mathbf{A}\right)}{p\left({\mathit{y}}_{\mathrm{0}:K}\right)}}.\end{array}\end{array}$$

Nonetheless, maximising Eq. (16) rigorously yields the maximum a posteriori of the joint variables $\mathbf{A},{\mathit{x}}_{\mathrm{0}:K}$. The cost function associated with this joint pdf is by definition $\mathcal{J}(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K})=-\ln \left(p\right(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K}\left|{\mathit{y}}_{\mathrm{0}:K}\right))$. Because Eq. (14) is Markovian and given the Gaussian form of both model and observational errors, the cost function reads as

$$\begin{array}{}\text{(17)}& \begin{array}{rl}\mathcal{J}(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K})=& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{k=\mathrm{0}}^K{∥{\mathit{y}}_k-{\mathbf{H}}_k\left({\mathit{x}}_k\right)∥}_{{\mathit{r}}_k^{-\mathrm{1}}}^{\mathrm{2}}\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{k=\mathrm{1}}^K{∥{\mathit{x}}_k-{\mathbf{F}}_{\mathbf{A}}^{k-\mathrm{1}}\left({\mathit{x}}_{k-\mathrm{1}}\right)∥}_{{\mathbf{Q}}_k^{-\mathrm{1}}}^{\mathrm{2}}\\ & -\ln p\left({\mathit{x}}_{\mathrm{0}}\right|\mathbf{A})-\ln p(\mathbf{A}),\end{array}\end{array}$$

up to a constant depending on Q_1:K and r_0:K only. The vector norm ∥z∥_P is defined as $\sqrt{{\mathit{z}}^{\mathbf{T}}\mathbf{P}\mathit{z}}$. This is the cost function of a weak constraint 4D-Var (see Sect. 2.4.3.2 of Asch et al., 2016) with A and x_0:K as control variables.

In the case where the reference model is fully and directly observed, i.e. H_k≡I_x, and in the absence of observation noise, i.e. r_k≡0, we have ${\mathit{x}}_{\mathrm{0}:K}\equiv {\mathit{y}}_{\mathrm{0}:K}$ and the cost function simplifies to

$$\begin{array}{ll}{\displaystyle }\mathcal{J}\left(\mathbf{A}\right)=& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{k=\mathrm{1}}^K{∥{\mathit{y}}_k-{\mathbf{F}}_{\mathbf{A}}^{k-\mathrm{1}}\left({\mathit{y}}_{k-\mathrm{1}}\right)∥}_{{\mathbf{Q}}_k^{-\mathrm{1}}}^{\mathrm{2}}\\ \text{(18)}& {\displaystyle }& {\displaystyle }-\ln p\left({\mathit{y}}_{\mathrm{0}}\right|\mathbf{A})-\ln p(\mathbf{A}),\end{array}$$

where y_0:K is the fully and perfectly observed state trajectory of the reference model. This is notably similar to a traditional least-square function used in machine and deep learning regression. This connection between machine learning and data assimilation cost functions had been previously put forward by Hsieh and Tang (1998) and Abarbanel et al. (2018), although in a different form. Reciprocally, when the aforementioned hypotheses of noiseless and complete observations do not hold, Eq. (17) can be seen as a natural data assimilation extension of Eq. (18). Note that Eq. (18) only depends on the sequence Q_1:K. If, in addition, the dependence on $p({\mathit{y}}_{\mathrm{0}},\mathbf{A})=p\left({\mathit{y}}_{\mathrm{0}}\right|\mathbf{A}\left)p\right(\mathbf{A})$ is neglected in Eq. (18), then the maximum a posteriori should not depend on a global rescaling of Q_1:K.

The data assimilation system is represented in Fig. 1 as a hidden Markov chain model. This Bayesian view highlights the choice that must be made for r_0:K and/or Q_1:K and provides an interpretation in terms of errors. Furthermore, one could implement an objective estimation of these error statistics as in Pulido et al. (2018).

2.5 Gradients and adjoint of the representation

To efficiently minimise the cost function Eq. (17) with a gradient-based optimisation tool, we need to analytically derive the gradient of Eq. (17) with respect to both A and x_0:K. As for x_0:K, we have

$$\begin{array}{}\text{(19a)}& {\displaystyle }\begin{array}{rl}{\mathrm{\nabla }}_{{\mathit{x}}_{\mathrm{0}}}\mathcal{J}=& -{\left({\mathrm{\nabla }}_{{\mathit{x}}_{\mathrm{0}}}{\mathbf{H}}_{\mathrm{0}}\right)}^{\mathrm{T}}{\mathit{r}}_{\mathrm{0}}^{-\mathrm{1}}{\mathit{\delta }}_{\mathrm{0}}-{\left({\mathrm{\nabla }}_{{\mathit{x}}_{\mathrm{0}}}{\mathbf{F}}_{\mathbf{A}}^{\mathrm{0}}\right)}^{\mathrm{T}}{\mathbf{Q}}_{\mathrm{1}}^{-\mathrm{1}}{\mathbf{\Delta }}_{\mathrm{1}}\\ & -{\mathrm{\nabla }}_{{\mathit{x}}_{\mathrm{0}}}\ln p\left({\mathit{x}}_{\mathrm{0}}\right|\mathbf{A}),\end{array}\text{(19b)}& {\displaystyle }\begin{array}{rl}{\mathrm{\nabla }}_{{\mathit{x}}_k}\mathcal{J}=& -{\left({\mathrm{\nabla }}_{{\mathit{x}}_k}{\mathbf{H}}_k\right)}^{\mathrm{T}}{\mathit{r}}_k^{-\mathrm{1}}{\mathit{\delta }}_k-{\left({\mathrm{\nabla }}_{{\mathit{x}}_k}{\mathbf{F}}_{\mathbf{A}}^k\right)}^{\mathrm{T}}{\mathbf{Q}}_{k+\mathrm{1}}^{-\mathrm{1}}{\mathbf{\Delta }}_{k+\mathrm{1}}\\ & +{\mathbf{Q}}_k^{-\mathrm{1}}{\mathbf{\Delta }}_k,\text{for}\mathrm{1}\le k\le K-\mathrm{1},\end{array}\text{(19c)}& {\displaystyle }{\mathrm{\nabla }}_{{\mathit{x}}_K}\mathcal{J}=-{\left({\mathrm{\nabla }}_{{\mathit{x}}_K}{\mathbf{H}}_K\right)}^{\mathrm{T}}{\mathit{r}}_K^{-\mathrm{1}}{\mathit{\delta }}_K+{\mathbf{Q}}_K^{-\mathrm{1}}{\mathbf{\Delta }}_K,\end{array}$$

where ${\mathit{\delta }}_k={\mathit{y}}_k-{\mathbf{H}}_k\left({\mathit{x}}_k\right)$ for $\mathrm{0}\le k\le K$ and ${\mathbf{\Delta }}_k={\mathit{x}}_k-{\mathbf{F}}_{\mathbf{A}}^{k-\mathrm{1}}\left({\mathit{x}}_{k-\mathrm{1}}\right)$ for $\mathrm{1}\le k\le K$; ${\mathrm{\nabla }}_{x_k}{\mathbf{F}}_{\mathbf{A}}^k$ is the tangent linear operator of the resolvent ${\mathbf{F}}_{\mathbf{A}}^k$ computed at x_k for $\mathrm{0}\le k<K$; ${\mathrm{\nabla }}_{x_k}{\mathbf{H}}_k$ is the tangent linear operator of the observation operator H_k computed at x_k for $\mathrm{0}\le k\le K$. As for A, we have

$$\begin{array}{}\text{(20)}& {\mathrm{\nabla }}_{\mathbf{A}}\mathcal{J}=-\sum _{k=\mathrm{1}}^K{\mathit{\delta }}_k^{\mathrm{T}}{\mathbf{Q}}_k^{-\mathrm{1}}{\mathrm{\nabla }}_{\mathbf{A}}{\mathbf{F}}_{\mathbf{A}}^{k-\mathrm{1}}\left({\mathit{x}}_{k-\mathrm{1}}\right)-{\mathrm{\nabla }}_{\mathbf{A}}\ln p\left(\mathbf{A}\right),\end{array}$$

assuming x₀ is independent of A. Hence, a key technical aspect of the problem is to compute the tangent linear and adjoint operators required by these gradients. In this paper, we assume that the adjoints ${\left({\mathrm{\nabla }}_{{\mathit{x}}_k}{\mathbf{H}}_k\right)}^{\mathrm{T}}$ of the tangent linear operators of the observation operators are known, for instance if the latter are linear as in Sect. 4.

The computations of the gradients and the required adjoints are developed in Appendix B. These technicalities can be skipped since they are not required to understand the method. Nonetheless, they are critical to its numerical efficiency.

3 Discussion of the theoretical points

In this section, we discuss the prior pdf p(A), the optimisation of the cost function $\mathcal{J}(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K})$, and the connections with deep learning techniques.

3.1 Prior information on the reference model

The goal is either to reconstruct an ODE for the reference model, characterised by the coefficients A through ϕ_A, or to build a surrogate model of it. The estimation of x_0:K is then accessory even though factually critical to the estimation of A. The alternative would have been to consider the estimation of x_0:K as the primary problem, under model error of a prescribed ODE form, the estimation of A becoming accessory. In both cases, but particularly in the latter one, one may benefit from an informative prior pdf p(A).

The prior pdf p(A) can be used to encode any prior knowledge on the reference model, such as pieces of it that would be known. Indeed, p(A) can formally quantity the uncertainty associated with any part of the surrogate model. For instance, assume that the reference model is partially identifiable, which means that part of the reference model could be represented by an up to bilinear flow rate of the form Eq. (2) and Eq. (4). Moreover, assume that there is one such part of the reference model which is known, i.e. that elements of A are actually known, while others need to be estimated. Then, the known coefficients can formally be encoded in p(A) with Dirac factors. In practice it could be implemented as a constrained optimisation problem, for instance using an augmented Lagrangian, in order to avoid significantly altering the gradients with respect to A. More generally, assigning a non-trivial prior likelihood, such as a Gaussian one for A, is certainly appealing but may not be practical.

3.2 Numerical optimisation: issues and solutions

The success of the optimisation of $\mathcal{J}(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K})$ depends above all on the ability to evaluate it robustly. In particular, it depends on the stability of the numerical integration scheme ${\mathit{x}}^{\prime }={\mathbf{f}}_{\mathbf{A}}\left(\mathit{x}\right)$. In this paper, we chose to rely on one-step explicit schemes which are much simpler to describe and efficient to integrate (a family to which the RK schemes of any N_RK belong). These schemes are 0-stable, which means that the finite time error growth goes to zero as the integration step goes to zero. But, as a major drawback, they have a limited absolute (or A-)stability domain (see e.g. chapters 5 and 6 of Gautschi, 2012). For a given state trajectory, there exists a stability domain ${\mathcal{D}}_{\mathrm{s}}\in {\mathbb{R}}^{N_x\times N_p}$ out of which the evaluation of $\mathcal{J}(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K})$ is hazardous. A failure to evaluate the cost function also depends on the number of integration steps since the instabilities are likely to increase exponentially with $N_{\mathrm{c}}^k$.

This says that, in the absence of a strong prior p(A), it is safer to start with A=0 likely to lie close to 𝒟_s. Alternatively, if stability constraints are known about A, they could be encoded in p(A). It also says that we should strike an empirical compromise between the composition numbers $N_{\mathrm{c}}^k$ and the easiness in evaluating $\mathcal{J}(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K})$. On the one hand, the larger $N_{\mathrm{c}}^k$, the more the iterates of A in the optimisation must be kept confined in 𝒟_s. On the other hand, the longer $N_{\mathrm{c}}^k$, the broader the class of achievable resolvents and hence the ability to build a good surrogate. Moreover, the higher the stability of the integration scheme, the larger 𝒟_s, and the easier the optimisation in spite of an increase in its numerical cost.

As for the sensitivity on K, the longer the time window, the more observations are available to constrain the problem. However, the longer K, the higher the chances of having a significant instability: the chances of a successful integration typically decrease exponentially with the length K.

This stability issue can be somehow alleviated by normalising the observations y_k by their mean and variance in order to avoid excessively large value ranges of the regressors. This will not change the fundamental stability of the schemes, yet may delay the occurrences of instabilities due to the nonlinear terms.

Moreover, instabilities can significantly be mitigated by replacing the monomials with smoothed or truncated ones:

$$\begin{array}{}\text{(21)}& \mathit{r}\left(\mathit{x}\right)=\left[{\left\{\mathit{\zeta }\left({\stackrel{\mathrm{̃}}{x}}_n\right)\mathit{\zeta }\left({\stackrel{\mathrm{̃}}{x}}_m\right)\right\}}_{(n,m)\in \stackrel{\mathrm{̃}}{\mathcal{P}}}\right].\end{array}$$

One can for instance choose $\mathit{\zeta }\left(x\right)=\mathit{\lambda }\tanh (x/\mathit{\lambda })$, in order to cut off too large values of $\left|x\right|$ and hence delay the growth of instabilities. The parameter λ>0 is roughly chosen as the typical maximum amplitude of $\left|x\right|$ as approximately inferred from the observations. If tanh is deemed to be numerically too costly, one can choose instead $\mathit{\zeta }\left(x\right)=-\mathit{\lambda }{\mathrm{1}}_{]-\mathrm{\infty },-\mathit{\lambda }]}+x{\mathrm{1}}_{[-\mathit{\lambda },\mathit{\lambda }]}+\mathit{\lambda }{\mathrm{1}}_{[\mathit{\lambda },+\mathrm{\infty }[}$ or more generally $\mathit{\zeta }\left(x\right)=(-\mathit{\lambda }+\mathit{\epsilon }(x+\mathit{\lambda }\left)\right){\mathrm{1}}_{]-\mathrm{\infty },-\mathit{\lambda }]}+x{\mathrm{1}}_{[-\mathit{\lambda },\mathit{\lambda }]}+(\mathit{\lambda }+\mathit{\epsilon }(x-\mathit{\lambda }\left)\right){\mathrm{1}}_{[\mathit{\lambda },+\mathrm{\infty }[}$, with $\mathrm{0}\le \mathit{\epsilon }\ll \mathrm{1}$ a small trend.

This latter change in variables is the one implemented for all numerical applications described in Sect. 4, together with the normalisation. From these experiments, we learned that these tricks often turned critical in the first iterates of the optimisation when the estimate of A progressively migrated to the A-stability domain. After a few iterations, however, the integrations are stabilised and the nonlinear regime of the truncations in Eq. (21) is not tapped into anymore.

3.3 Connection and analogies with deep learning architectures

It has recently been advocated that residual deep learning architectures of neural networks can roughly be interpreted as dynamical systems (e.g. Weinan, 2017; Chang et al., 2018). Each layer of the network contributes marginally to the output, so that there exists an asymptotic continuum limit representation of the neural network. Furthermore, as mentioned in the introduction, Wang and Lin (1998) and Fablet et al. (2018) have shown that the architecture of the network can follow that of an integration scheme.

By contrast, we have started here from a pure dynamical system standpoint and proposed to use data assimilation techniques. In order to explore complex model resolvents, applied to each interval $[t_k,t_{k+\mathrm{1}}]$ between observations, we need the composition of N_c integration steps. In particular, this allows the resolvent to exhibit more realistic long-range correlations. Even when using a reasonably small stencil, long-range correlations will arise as a result of the integration steps. Nonetheless, the stencil might not be too small so as to model discretised higher-order differential operators. As noted by Abarbanel et al. (2018), each application of f_A could be seen as a layer of the neural network. Moreover, within such a layer, there are sublayers corresponding to the steps of the integration scheme. The larger N_c is, the deeper this network is, and the richer the class of resolvents is to optimise on.

Following this analogy, the analysis step where $\mathcal{J}(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K})$ is optimised can be called the training phase. Backpropagation in the network, as coined in machine learning (Goodfellow et al., 2016), corresponds to the computation of the gradient of the network with respect to A and of the model adjoint derived in Sect. 2. This is a shortcut for the use of machine learning software libraries such as TensorFlow or PyTorch (see Appendix C for a brief discussion).

Because of our complete control of the backpropagation, we hope for a gain in efficiency. However, our method does not have the flexibility of deep learning through established tools. For instance, addition of extra parameters, adaptive batch normalisation, and dropouts are not granted in our approach without further considerations.

Convolutional layers play the role of localisation in neural architecture. In our approach this role is played by the locality assumption and its stencil prescription. Recall that a tight stencil does not prevent longer-range correlations that are built up through the integration scheme and their composition. This is similar to stacking several convolutional layers to account for multiple scales from the reference model which the neural network is meant to learn from.

Finally, we note that, as opposed to most practical deep learning strategies with a huge amount of weights to estimate, we have reduced the number of control variables (i.e. A) as much as possible.

4 Numerical illustrations

4.1 Model setup and forecast skill

In this section, we shall consider four low-order chaotic models defined on a physical one-dimensional space, except for L63, which is 0-dimensional. They will serve as reference models.

1. The L63 model as defined by the ODEs:

   $$\begin{array}{}\text{(22a)}& {\displaystyle \frac{\mathrm{d}{x}_{\mathrm{0}}}{\mathrm{d}t}}& {\displaystyle }=\mathit{\sigma }(x_{\mathrm{1}}-x_{\mathrm{0}}),\text{(22b)}& {\displaystyle \frac{\mathrm{d}{x}_{\mathrm{1}}}{\mathrm{d}t}}& {\displaystyle }=\mathit{\rho }{x}_{\mathrm{0}}-x_{\mathrm{1}}-x_{\mathrm{0}}{x}_{\mathrm{2}},\text{(22c)}& {\displaystyle \frac{\mathrm{d}{x}_{\mathrm{2}}}{\mathrm{d}t}}& {\displaystyle }=\mathit{\rho }{x}_{\mathrm{0}}{x}_{\mathrm{1}}-\mathit{\beta }{x}_{\mathrm{2}},\end{array}$$

   with the canonical values $(\mathit{\sigma },\mathit{\rho },\mathit{\beta })=(\mathrm{10},\mathrm{28},\mathrm{8}/\mathrm{3})$. Its Lyapunov time¹ is about 1.10. Besides its intrinsic value, this model is introduced for benchmarking against Fablet et al. (2018). It is integrated using an RK4 scheme with δt_r=0.01 as the integration time step.

2. The L96 model as defined by ODEs defined over a periodic domain of variables indexed by $n=\mathrm{0},\mathrm{\dots },N_x-\mathrm{1}$ where N_x=40:

   $$\begin{array}{}\text{(23)}& {\displaystyle \frac{\mathrm{d}{x}_n}{\mathrm{d}t}}=(x_{n+\mathrm{1}}-x_{n-\mathrm{2}})x_{n-\mathrm{1}}-x_n+F,\end{array}$$

   where $x_{N_x}=x_{\mathrm{0}}$, $x_{-\mathrm{1}}=x_{N_x-\mathrm{1}}$, $x_{-\mathrm{2}}=x_{N_x-\mathrm{2}}$, and F=8. This model is an idealised representation of a one-dimensional latitude band of the Earth's atmosphere. Its Lyapunov time is 0.60. It is integrated using the RK4 scheme and with δt_r=0.05.

3. The KS model, as defined by the PDE:

   $$\begin{array}{}\text{(24)}& {\displaystyle \frac{\partial x}{\partial t}}=-x{\displaystyle \frac{\partial x}{\partial \mathit{\alpha }}}-{\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial {\mathit{\alpha }}^{\mathrm{2}}}}-{\displaystyle \frac{{\partial }^{\mathrm{4}}x}{\partial {\mathit{\alpha }}^{\mathrm{4}}}},\end{array}$$

   over the periodic domain $\mathit{\alpha }\in [\mathrm{0},\mathrm{32}\mathit{\pi }]$ on which we apply a spectral decomposition with N_x=128 modes. The Lyapunov time of our KS model is 10.2 time units. This model is of interest because, even though it has dynamical properties comparable to that of L96, it is much steeper, so that much more stringent numerical integration schemes are required to efficiently integrate it. It is defined by a PDE, not an ODE system. It is integrated using the EDTRK4 scheme (Kassam and Trefethen, 2005) and δt_r=0.05.

4. The two-scale Lorenz model (L05III, Lorenz, 2005) is given by the two-scale ODEs:

   $$\begin{array}{}\text{(25a)}& {\displaystyle \frac{\mathrm{d}{x}_n}{\mathrm{d}t}}& {\displaystyle }={\mathit{\psi }}_n^{+}\left(\mathit{x}\right)+F-h{\displaystyle \frac{c}{b}}\sum _{m=\mathrm{0}}^{\mathrm{9}}{u}_{m+\mathrm{10}n},\text{(25b)}& {\displaystyle \frac{\mathrm{d}{u}_m}{\mathrm{d}t}}& {\displaystyle }={\displaystyle \frac{c}{b}}{\mathit{\psi }}_m^{-}\left(b\mathbf{u}\right)+h{\displaystyle \frac{c}{b}}{x}_{m/\mathrm{10}},\text{(25c)}& {\displaystyle }{\mathit{\psi }}_n^{\pm }\left(\mathit{x}\right)& {\displaystyle }=x_{n\mp \mathrm{1}}(x_{\pm \mathrm{1}}-x_{n\mp \mathrm{2}}),\end{array}$$

   for $n=\mathrm{0},\mathrm{\dots },N_x-\mathrm{1}$ with N_x=36 and $m=\mathrm{0},\mathrm{\dots },N_u-\mathrm{1}$ with N_u=360. The indices apply periodically over their domain; m∕10 stands for the integer division of m by 10. We use the original values for the parameters: c=10 for the timescale ratio, b=10 for the space-scale ratio, h=1 for the coupling, and F=10 for the forcing. When uncoupled (h=0), the Lyapunov time of the slow variables x sector of the model Eq. (25) is 0.72, which will be the key timescale when focusing on the slow variables (see e.g. Carlu et al., 2019).

   This model is of interest because the variable u is meant to represent unresolved scales and hence model error when only considering the slow variables x. For this reason, it has been used in data assimilation papers focusing on estimating model error (e.g. Mitchell and Carrassi, 2015; Pulido et al., 2018). It is integrated with an RK4 scheme and δt_r=0.005 since it is steeper than the L96 model.

The numerical experiments consist of three main steps. First, the truth is generated, i.e. a trajectory of the reference model is computed. The reference model equations are supposed to be unknown, but the trajectory is observed through Eq. (13) to generate the observation vector sequence y_0:K.

Next, estimators of the ODE model and state trajectory x_0:K are learned by minimising the cost function $\mathcal{J}(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K})$. We choose to minimise it using an implementation of the quasi-Newton BFGS algorithm (Byrd et al., 1995), which critically relies on the gradients obtained in Sect. 2. The default choices for the initial ODE model are A=0 and x_0:K defined as the space-wise linear interpolation of y_0:K. Note that the minimisation could converge to a local minimum, which may or may not yield satisfactory estimates.

Finally, we can make forecasts using the tentative optimal ODE model A^⋆ obtained from the minimisation. With a view to comparing it to the reference model used to generate the data, we will consider a set of forecasts with (approximately) independent initial conditions. Both the reference model and the surrogate one will be forecasted from these initial conditions. The departure from their trajectories, as measured by a root mean square error (RMSE) over the observed variables, will be computed for several forecast lead times. The RMSE is then averaged over all the initial conditions. We will also display the state trajectories of the reference and surrogate models starting from one of the initial conditions.

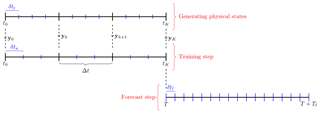
The integration time step of the truth (reference model) is δt_r over the time window [t₀,t_K]. This parameter only matters for the reference model integration since only the training time steps $t_{k+\mathrm{1}}-t_k$ and the output of the model y_0:K (which may include knowledge of the observation operator) are known to the observer.

The integration time step of the surrogate model within the training time window [t₀,t_K] is δt_a. It is assumed to be an integer divisor of the training time step $\mathrm{\Delta }t=t_{k+\mathrm{1}}-t_k$, supposed to be constant, i.e. Δt∕δt_a is a constant integer and the number of compositions N_c, and that is why the index k on $N_{\mathrm{c}}^k$ has been dropped. The integration time step of the surrogate model within the forecast time window $[T,T+T_{\mathrm{f}}]$ is denoted δt_f. Note that δt_a and δt_f can be distinct and that they are critical to the stability of the training and the forecast step, respectively.

The three steps of the numerical experiments are depicted in Fig. 2. Except when explicitly mentioned, the prior p(A) is disregarded, which means that no explicit regularisation on A is introduced.

Figure 2 Schematic of the three steps of the experiments, with the associated time steps (see main text). The beginning of the forecast window may or may not coincide with the end of the training window. The lengths of the segments δt_r, δt_a, and δt_f are arbitrary in this schematic.

4.2 Inferring the dynamics from dense and noiseless observations: perfectly identifiable models

In the first couple of experiments, we consider a densely observed² reference model with noiseless observations. In this case, H_k is the identity operator, i.e. each grid point value is observed, and r_k≡0 so that a uniform rescaling of the Q_k, all chosen to be I_x, is irrelevant, assuming $p({\mathit{y}}_{\mathrm{0}},\mathbf{A})=p\left({\mathit{y}}_{\mathrm{0}}\right|\mathbf{A}\left)p\right(\mathbf{A})$ can be neglected, which is hypothesised here and is generally true for large K. Moreover, we use the same numerical scheme with the same integration time step to generate the reference model trajectory as the one used by the surrogate model. In principle, we should be able to retrieve the reference model, since the reference is identifiable, meaning that it belongs to the set of all possible surrogate models.

Let us first experiment with the L63 model, using an RK4 integration scheme, with Δt=0.01 and K=10⁴ (this corresponds to about 91 Lyapunov times). We have N_x=3 and N_p=10. We choose $\mathit{\delta }{t}_{\mathrm{a}}=\mathit{\delta }{t}_{\mathrm{f}}=\mathrm{0.01}$. A convergence to the highest possible precision is achieved after about 120 iterations. The cost function value reaches 0 to machine precision at A^⋆. The estimated A is given by ${\mathbf{A}}_{\mathrm{a}}={\mathbf{A}}^{\star }/\mathit{\delta }{t}_{\mathrm{a}}$, because, as mentioned above, the optimised A matrix absorbs the time step. The accuracy of A_a is measured by the uniform norm ${∥{\mathbf{A}}_{\mathrm{a}}-{\mathbf{A}}_{\mathrm{r}}∥}_{\mathrm{\infty }}$, i.e. the absolute values of the entries of the difference A_a−A_r, where A_r is the matrix of the flow rate of L63 (including the zero coefficients). We obtain ${∥{\mathbf{A}}_{\mathrm{a}}-{\mathbf{A}}_{\mathrm{r}}∥}_{\mathrm{\infty }}=\mathrm{8.46}\times {\mathrm{10}}^{-\mathrm{18}}$. To compute the RMSE as a function of the forecast lead time, we average over N_e=10³ runs (each one starting from a difference initial condition). The RMSE (not shown) starts significantly, diverging from 0 after 16 Lyapunov time units, and reaches a saturation for a lead time of 23 Lyapunov times.

A similar experiment is carried out with the L96 model, using an RK4 integration scheme, with Δt=0.05 and K=50 (this corresponds to about 4.2 Lyapunov times). We choose here to implement the locality and homogeneity assumptions (see Sect. 2.2.1 and 2.2.2). The stencil has a width of 5 (i.e. the local grid points with two points on its left and two points on its right). We have N_x=40, N_p=161, and N_a=18. We choose $\mathit{\delta }{t}_{\mathrm{a}}=\mathit{\delta }{t}_{\mathrm{f}}=\mathrm{0.05}$. Through the minimisation, the main coefficients of the L96 model (forcing F, advection terms, dissipation) are retrieved with a precision of a least $\mathrm{8.88}\times {\mathrm{10}}^{-\mathrm{15}}$.

To compute the RMSE as a function of the forecast lead time, we average over N_e=10³ runs. The RMSE starts significantly, diverging from 0 after 12 Lyapunov times, and reaches a saturation for a lead time of 25 Lyapunov times.

4.3 Inferring the dynamics from dense and noiseless observations: non-identifiable models

In this second couple of experiments, we consider again a densely observed reference model with noiseless observations. The reference model trajectory is generated by the L96 model (N_x=40) integrated with the RK4 scheme, with Δt=0.05 and K=50.

As opposed to the reference model, in these non-identifiable model experiments, the surrogate model is based on the RK2 scheme, with N_c compositions. We choose to implement the locality and homogeneity assumptions, with a stencil of width 5. We have N_p=161 and N_a=18. We choose $\mathit{\delta }{t}_{\mathrm{a}}=\mathit{\delta }{t}_{\mathrm{f}}=\mathrm{\Delta }t/N_{\mathrm{c}}$. In all the cases, the convergence is reached within a few dozens of iterations. The error on the coefficients of A (i.e. ${∥{\mathbf{A}}_{\mathrm{a}}-{\mathbf{A}}_{\mathrm{r}}∥}_{\mathrm{\infty }}$) is about $\mathrm{4}\times {\mathrm{10}}^{-\mathrm{2}}$ but with the dominant contribution from F. The RMSE as a function of the forecast lead time is computed for $N_{\mathrm{c}}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}$ and is shown in Fig. 3. The error is reduced as N_c is increased. But the improvement saturates at about N_c=5.

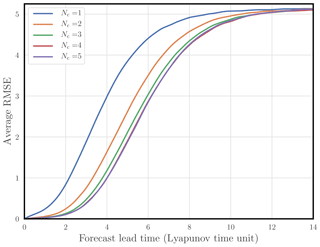
Figure 3 Average RMSE of the surrogate model (L96 with an RK2 structure) compared to the reference model (L96 with an RK4 integration scheme) as a function of the forecast lead time (in Lyapunov time unit) for an increasing number of compositions.

Figure 4 shows the trajectories of the reference and surrogate models starting from the same initial condition, as well as their difference, as a function of the forecast lead time. Their divergence becomes significant after 4 Lyapunov times and saturates after 8 Lyapunov times.

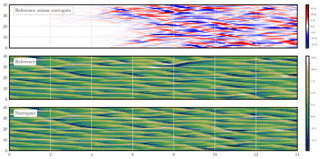
Figure 4 Density plot of the L96 reference and surrogate model trajectories, as well as their difference trajectory, as a function of the forecast lead time (in Lyapunov time unit). The observations are noiseless and dense; the model is not identifiable.

Next, the reference model trajectory is generated by the KS model (N_x=128) integrated with the ETDRK4 scheme, with Δt=0.05 and K=50 (this corresponds to about 0.25 Lyapunov time). We choose to implement the locality and homogeneity assumptions, with a stencil of width 9. The surrogate model is based on the RK4 scheme, with N_c=2 compositions. Note that in this experiment, the reference and surrogate models and their integration schemes significantly differ. We have N_p=769 and N_a=45. We choose $\mathit{\delta }{t}_{\mathrm{a}}=\mathrm{\Delta }t/N_{\mathrm{c}}$ and $\mathit{\delta }{t}_{\mathrm{f}}={\mathrm{10}}^{-\mathrm{3}}$. The forecast time step δt_f is somehow smaller than δt_a because the KS equations are stiff and so will the surrogate model be. This emphasises once again that we have learned about the intrinsic flow rate of the reference model and not a resolvent thereof. Alternatively, we could use a more robust integration scheme than RK4 such as ETDRK4 for the forecast.

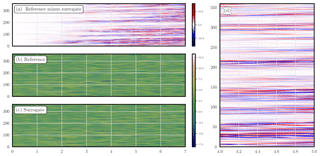
Figure 5 shows the trajectories of the reference and surrogate models starting from the same initial condition, as well as their difference, as a function of the forecast lead time, for a stencil of 9. Their divergence becomes significant after 4 Lyapunov times and saturates after 8 Lyapunov times.

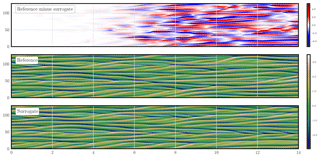
Figure 5 Density plot of the KS reference and surrogate model trajectories, as well as their difference trajectory, as a function of the forecast lead time (in Lyapunov time unit). The observations are noiseless and dense; the model is not identifiable.

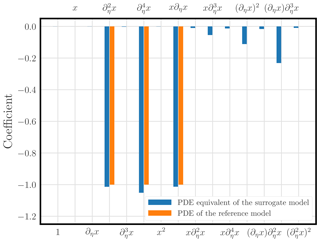
To check whether the PDE of the KS model could be retrieved in spite of the differences in the method of integrations and representations, we have computed a Taylor expansion of all monomials in the surrogate ODE flow rate up to order 4 so as to obtain an approximately PDE equivalent. The coefficients of this PDE (up to order 4 in the expansion) are displayed in Fig. 6 and compared to the coefficients of the reference model's PDE. The match is good and the terms $-x{\partial }_{\mathit{\alpha }}x$, $-{\partial }_{\mathit{\alpha }}^{\mathrm{2}}x$, and $-{\partial }_{\mathit{\alpha }}^{\mathrm{4}}x$ are correctly identified as the dominant ones. Nonetheless, there are three non-negligible coefficients for higher-order terms that either might have been generated by the Taylor expansion or may originate from a degeneracy among the higher-order operators, or may simply be identified with a shortcoming of our specific ODE representation.

Figure 6 Coefficients of the surrogate PDE model (blue) resulting from the expansion of the surrogate ODEs and compared to the reference PDE's coefficients (orange).

4.4 Inferring the dynamics from partial and noisy observations

We come back to the L96 model, which is densely observed but with noisy observations that are generated using an independently identically distributed normal noise. The surrogate model is based on an RK4 scheme N_c=1 and a stencil of length 5, which makes the reference model identifiable. In this case, the outcome theoretically depends on the choice for r_k and Q_k, given that Eq. (17) is now used instead of Eq. (18). For the sake of simplicity, we have chosen them to be of the scalar forms ${\mathit{r}}_k\equiv {\mathit{\sigma }}_y^{\mathrm{2}}{\mathbf{I}}_y$ and Q_k≡qI_x. In these synthetic experiments, σ_y is supposed to be known, while q is not. We only have a qualitative view of the potential mismatch between the reference and the surrogate model. Moreover, a Gaussian additive noise might not even be the best statistical model for such error. Nonetheless holding to the above Gaussian assumptions for model error, the optimal value of q could be determined using an empirical Bayes approach based on, for instance, the expectation–maximisation technique in order to determine the maximum a posteriori of the conditional density of q (see e.g. Dreano et al., 2017; Pulido et al., 2018). The use of advanced methods of that sort to estimate model error will be considered in future works, while, in the following, we have chosen values of q that yield near-to-optimal skill scores (typically $q\in [{\mathrm{10}}^{-\mathrm{4}},\mathrm{1}]{\mathit{\sigma }}_y^{\mathrm{2}}$). Moreover, note that we have chosen the relatively small K=50. While we expect increasing K to be beneficial, especially with noisy observations, it would force us to address issues related to weak constraint 4D-Var optimisation for long time windows, a topic which is also beyond the scope of this paper. Preliminary results on this aspect are nonetheless discussed later in this section.

Figure 7 shows the forecast skill of the surrogate model as a function of the forecast lead time and for increasing noise in the observations.

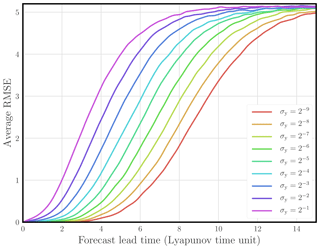
Figure 7 Average RMSE of the surrogate model (L96 with an RK4 structure) compared to the reference model (L96 with an RK4 integration scheme) as a function of the forecast lead time (in Lyapunov time unit) for a range of observation error standard deviations σ_y.

Even though, in this configuration, the model is identifiable, the reference value A₀ for A may not correspond to a minimum of the cost function. The cost function might have several local minima. As a consequence, there is no guarantee, starting from a non-trivial initial value for A, that the model will be identified. Indeed, as seen in Fig. 7, the forecast skill degrades significantly as the observation error standard deviation is increased.

This is confirmed by Fig. 8, where the precisions in identifying the model, measured by either the spectral norm ${∥{\mathbf{A}}_{\mathrm{0}}-\mathbf{A}∥}_{\mathrm{2}}$ or the uniform norm ${∥{\mathbf{A}}_{\mathrm{0}}-\mathbf{A}∥}_{\mathrm{\infty }}$, are plotted as functions of the observation error standard deviation.

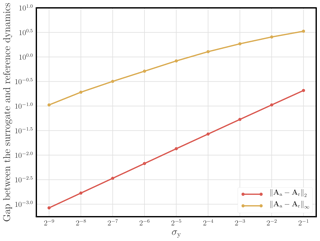
Figure 8 Gap between the surrogate (L96 with an RK4 structure) and the (identifiable) reference dynamics (L96 with an RK4 integration scheme) as a function of the observation error standard deviation σ_y. Note the use of logarithmic scales.

Using the same setup, we have also reduced the number of observations. The observations of grid point values are regularly spaced and shifted by one grid cell at each observation time step. The initial A in the optimisation remains 0, while the initial state x_0:K is taken as a cubic spline interpolation of the observations over the whole surrogate model grid.

If the observations are noiseless, the reference model is easily retrieved to a high precision down to a density of 1 site over 4. If the observations are noisy, the performance slowly degrades when the density is decreased down to about 1 site over 4, below which the minimisation, trapped in a deceiving local minimum, yields an improper surrogate model.

We would like to point out that in the case of noiseless observations, the performance depends little on the length of the training window, beyond a relatively short length, typically K=50. However, in the presence of noisy observations, the overall performance improves with longer K, as expected since the information content of the observations linearly increases with the length of the window.

Figure 9 displays the values of the coefficients in A with respect to the minimisation iteration index for the noiseless and fully observed case. As expected, 4 coefficients converge to the value specified by the exact L96 flow rate, while the 14 other coefficients collapse to 0.

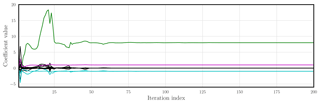
Figure 9 L96 is the reference model, which is fully observed without noise: plot of the N_a=18 coefficients of the surrogate model as a function of the minimisation iteration number. The coefficient of the forcing (F) is in green, the coefficients of the convective terms are in cyan, and the dampening coefficient is in magenta.

Figure 10 shows the same but in the significantly noisy case where σ_y=1 and with a significantly longer window K=5000 (about 417 Lyapunov times).

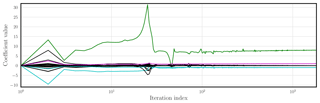
Figure 10 L96 is the reference model, which is fully observed with observation error standard deviation σ_y=1: plot of the N_a=18 coefficients of the surrogate model as a function of the minimisation iteration number. Note that the index axis is in logarithmic scale. The coefficient of the forcing (F) is in green, the coefficients of the convective terms are in cyan, and the dampening coefficient is in magenta.

Figure 11 Density plot of the L05III reference and surrogate model trajectories, as well as their difference trajectory, as a function of the forecast lead time (in Lyapunov time unit). Panel (d) shows a zoom of the difference between times 4 and 5.

4.5 Inferring reduced dynamics of a multiscale model

In this experiment, we consider the L05III model. With the locality and the homogeneity assumptions, the scalability is typically linear with the size of the system, and we actually consider the 10-fold model where N_x=360 and N_u=3600 to demonstrate that no issues were encountered when scaling up the method. The large-scale variable x of the reference model is noiselessly and fully observed over a short training window (K=50, which corresponds to about 0.35 Lyapunov time), i.e. all slow variable values are observed, whereas the short-scale variable u is not observed. The surrogate model is based on the RK4 scheme and N_c=2 compositions. We choose to implement the locality and homogeneity assumptions, with a stencil of width 5. We have N_p=161 and N_a=18. We choose $\mathit{\delta }{t}_{\mathrm{a}}=\mathit{\delta }{t}_{\mathrm{f}}=\mathrm{\Delta }t/N_{\mathrm{c}}$.

Figure 11 shows the trajectories of the reference and surrogate models starting from the same initial condition, as well as their difference, as a function of time.

The emergence of error, i.e. the divergence from the reference, appears as long darker stripes on the density plot of the difference (close to zero difference values appear as white or light colour). We argue that these stripes result from the emergence of sub-scale perturbations that are not properly represented by the surrogate model. Reciprocally there are long-lasting stripes of low error not yet impacted by sub-scale perturbations. As expected, and similarly to the L96 model, the perturbations are transported eastward, as shown by the upward tilt of the stripes in Fig. 11. Clearly, in this case, a flow rate of the form Eq. (2) could be insufficient. Adding a stochastic parametrisation with parameters additionally inferred might offer a solution, as in Pulido et al. (2018). Because of this mixed performance, the RMSE slowly degrades (compared to the other experiments reported so far) with the increase in the forecast lead time (not shown).

5 Conclusions

We have proposed to infer the dynamics of a reference model from its observation using Bayesian data assimilation, which is a new and original scope for data assimilation. Over a given training time window, the control variables are the state trajectory and the coefficients of an ODE representation for the surrogate model. We have chosen the surrogate model to be the composition of an explicit integration scheme (Runge–Kutta typically) applied to this ODE representation. Time invariance, space homogeneity, and locality of the dynamics can be enforced, making the method suitable for high-dimensional systems. The cost function of the data assimilation problem is minimised using the adjoint of the surrogate resolvent which is explicitly derived. Analogies between the surrogate resolvent and a deep neural network have been discussed as well as the impact of stability issues of the reference and surrogate dynamics.

The method has been applied to densely noiseless observed systems with identifiable reference models yielding a perfect reconstruction close to machine precision (L63 and L96 models). It has also been applied to densely or partially observed, identifiable or non-identifiable models with or without noise in the observations (L96 and KS models). For moderate noise and sufficiently dense observation, the method is successful in the sense that the forecast is accurate beyond several Lyapunov times. The method has also been used as a way to infer a reduced model for a multi-scale observed system (L05-III model). The reduced model was successful in emulating slow dynamics of the reference model, but could not properly account for the impact of the fast unresolved scale dynamics on the slow ones. A subgrid parametrisation would be required or would have to be inferred.

Two potential obstacles have been left aside on purpose but should later be addressed. First, the model error statistics have not been estimated. This could be achieved using for instance an empirical Bayesian analysis built on an ensemble-based stochastic expectation maximisation technique. This is an especially interesting problem since the potential discrepancy between the reference and the surrogate dynamics is in general non-trivial. Second, we have used relatively short training time windows. Numerical efficient training on longer windows will likely require use of advanced weak constraint variational optimisation techniques.

In this paper, only autonomous dynamics have been considered. We could at least partially extend the method to non-autonomous systems by keeping a static part for the pure dynamics and consider time-dependent forcing fields. We have not numerically explored non-homogeneous dynamics, but we have shown how to learn from them using non-homogeneous local representations.

A promising yet challenging path would be to consider implicit or semi-implicit schemes following for instance the idea in Chen et al. (2018). This idea is known in geophysical data assimilation as the continuous adjoint (see e.g. Bocquet, 2012). This would considerably strengthen the stability of the training and forecast steps at the cost of more intricate mathematical developments.

If observations keep coming after the training time window, then one can perform data assimilation using the ODE surrogate model of the reference model. This data assimilation scheme could only focus on state estimation or it could continue to update the ODE surrogate model for the forecast.

Appendix A: Parametrisation of ϕ_A for local representations defined over a circle

In this Appendix, we show how to parametrise ϕ_A assuming locality of the representation, in the case where it is defined over a periodic one-dimensional domain, i.e. a circle. It is of the generic form

$$\begin{array}{}\text{(A1)}& {\left[\mathbf{A}\cdot \mathit{r}\right]}_n=\sum _{p=\mathrm{0}}^{N_p-\mathrm{1}}{A}_{n,\mathit{\pi }(n,p)}{r}_p,\end{array}$$

where π(n,p) is an integer such that $\mathrm{0}\le \mathit{\pi }(n,p)<N_{\mathrm{a}}$. We can treat the bias, linear, and bilinear monomials separately into sectors, 0, 1, and 2, respectively. Let $\mathrm{0}\le a_i\le N_{\mathrm{a}}-\mathrm{1}$ be the indices which span the columns of A for each of the three sectors i and $\mathrm{0}\le p_i\le N_p-\mathrm{1}$ the indices which span the entries of r for each of the three sectors i. Then, Eq. (A1) can be more explicitly written as

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}{\left[\mathbf{A}\cdot \mathit{r}\right]}_n=& A_{n,a_{\mathrm{0}}\left(\mathrm{0}\right)}{r}_{p_{\mathrm{0}}\left(\mathrm{0}\right)}+\sum _{l=\mathrm{0}}^{\mathrm{2}L}{A}_{n,a_{\mathrm{1}}(n,l)}{r}_{p_{\mathrm{1}}(n,l)}\\ & +\sum _{l=\mathrm{0}}^L\sum _{m=\mathrm{0}}^{\mathrm{2}L-l}{A}_{n,a_{\mathrm{2}}(n,l,m)}{r}_{p_{\mathrm{2}}(n,l,m)},\end{array}\end{array}$$

where the dummy index l for the linear terms browses the stencil, and the dummy indices l,m for the bilinear monomials browse the stencil, in the same way as we did in Sect. 2.2.1 to enumerate them. By enumeration, we find the following.

• For the bias sector, we have p₀(0)=0 and a₀(0)=0.

• For the linear sector, we have $a_{\mathrm{1}}(n,l)=\mathrm{1}+l$ and $p_{\mathrm{1}}(n,l)=\mathrm{1}+[n+l-L]$, where [n] means the index in $[\mathrm{0},N_x-\mathrm{1}]$ congruent to n modulo N_x, in order to respect the periodicity of the domain.

• Finally, for the bilinear sector, we have $a_{\mathrm{2}}(n,l,m)=\mathrm{1}+\mathrm{2}L+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}l(\mathrm{4}L-l+\mathrm{1})+m$ and $p_{\mathrm{2}}(n,l,m)=\mathrm{1}+N_x+[n-L+m](\mathrm{1}+L)+l$.

We observe that these indices $a_{\mathrm{0}}\left(\mathrm{0}\right),a_{\mathrm{1}}(n,l)$, and $a_{\mathrm{2}}(n,l,m)$ do not depend on the site index n. They only indicate a relative position with respect to n. Hence, if homogeneity is additionally assumed, $A_{n,a_{\mathrm{0}}},A_{n,a_{\mathrm{1}}}$, and $A_{n,a_{\mathrm{2}}}$ do not depend on n anymore and A becomes a vector.

Appendix B: Computations of the gradients with respect to A and x_0:K

B1 Differentiation of the RK schemes

It will be useful in the following to consider the variation of each k_i, defined by Eq. (12b), with respect to either A or x:

$$\begin{array}{}\text{(B1)}& \mathit{\delta }{\mathbf{k}}_i=\mathit{\delta }{\mathit{\varphi }}_{\mathbf{A},i}+h\sum _{j=\mathrm{0}}^{i-\mathrm{1}}{\mathit{\alpha }}_{i,j}\left({\mathrm{\nabla }}_{{\mathit{x}}_i}{\mathit{\varphi }}_{\mathbf{A},i}\right)\mathit{\delta }{\mathbf{k}}_j,\end{array}$$

where ϕ_A,i is ϕ_A evaluated at ${\mathit{x}}_i^{\mathrm{RK}}\equiv \mathit{x}+h{\sum }_{j=\mathrm{0}}^{i-\mathrm{1}}{\mathit{\alpha }}_{i,j}{\mathbf{k}}_j$ and ${\mathrm{\nabla }}_{{\mathit{x}}_i}{\mathit{\varphi }}_{\mathbf{A},i}$ is the tangent linear operator with respect to x of ϕ_A evaluated at ${\mathit{x}}_i^{\mathrm{RK}}$. Equation (B1) can be written compactly in the form

$$\begin{array}{}\text{(B2)}& \mathbf{G}\mathit{\delta }\mathit{\kappa }=\mathit{\delta }\mathit{\phi },\end{array}$$

where G is the matrix of size (N_RKN_x)×(N_RKN_x) defined by its N_x×N_x blocks $[\mathbf{G}{]}_{i,j}={\mathbf{I}}_x-h{\mathit{\alpha }}_{i,j}{\mathrm{\nabla }}_{{\mathit{x}}_i}{\mathit{\varphi }}_{\mathbf{A},i}$, κ is the vector of size N_RKN_x which results from the stacking of the ${\mathbf{k}}_i\in {\mathbb{R}}^{N_x}$ for $\mathrm{0}\le i<N_{\mathrm{RK}}$, φ is the vector of size N_RKN_x which results from the stacking of the ϕ_A,i for $\mathrm{0}\le i<N_{\mathrm{RK}}$, and ${\mathbf{I}}_x\in {\mathbb{R}}^{N_x}$ is the identity matrix. The important point is that G is a lower triangular matrix and describes an iterative construction of the k_i. Moreover, the diagonal entries of G are 1 by construction so that G is invertible and

$$\begin{array}{}\text{(B3)}& \mathit{\delta }\mathit{\kappa }={\mathbf{G}}^{-\mathrm{1}}\mathit{\delta }\mathit{\phi }.\end{array}$$

This will be used to compute the variations of f_A(x) via Eq. (12a).

B2 Integration step

We first consider the situation when the observation interval corresponds to one integration time step of the surrogate model, i.e. $N_{\mathrm{c}}^k=\mathrm{1}$: ${\mathit{x}}^{\prime }={\mathbf{F}}_{\mathbf{A}}\left(\mathit{x}\right)={\mathbf{f}}_{\mathbf{A}}\left(\mathit{x}\right)$ with x≡x_k. As a result, the time index k can be omitted here. We will later consider the composition of several integration schemes (N_c≥2). Equation (12a) is written again but as

$$\begin{array}{}\text{(B4)}& {\mathbf{f}}_{\mathbf{A}}\left(\mathit{x}\right)=\mathit{x}+\mathbf{b}\mathit{\kappa },\end{array}$$

where $\mathbf{b}=\mathit{\beta }\otimes {\mathbf{I}}_x$ is the matrix of a size N_x×(N_RKN_x) tensor product of the vector β defined by ${\mathit{\beta }}^{\mathrm{T}}=({\mathit{\beta }}_{\mathrm{0}},\mathrm{\dots },{\mathit{\beta }}_{N_{\mathrm{RK}}-\mathrm{1}})$, i.e. the coefficients of the RK scheme as defined in Eq. (12a), with the state space identity matrix, and where κ is the vector of size N_RKN_x defined after Eq. (B2). Looking first at the gradient with respect to the state variable, and using Eq. (B3), we have

$$\begin{array}{}\text{(B5)}& {\mathrm{\nabla }}_{\mathit{x}}{\mathbf{f}}_{\mathbf{A}}={\mathrm{\nabla }}_{\mathit{x}}\mathit{x}+\mathbf{b}{\mathrm{\nabla }}_{\mathit{x}}\mathit{\kappa }={\mathbf{I}}_x+{\mathbf{bG}}^{-\mathrm{1}}{\mathrm{\nabla }}_{\mathit{x}}\mathit{\phi },\end{array}$$

which yields the adjoint operator

$$\begin{array}{}\text{(B6)}& {\left({\mathrm{\nabla }}_{\mathit{x}}{\mathbf{f}}_{\mathbf{A}}\right)}^{\mathrm{T}}={\mathbf{I}}_x+{\left({\mathrm{\nabla }}_{\mathrm{x}}\mathit{\phi }\right)}^{\mathrm{T}}{\mathbf{G}}^{-\mathrm{T}}{\mathbf{b}}^{\mathrm{T}}.\end{array}$$

Let us consider an arbitrary vector $\mathit{d}\in {\mathbb{R}}^{N_x}$; we have

$$\begin{array}{}\text{(B7)}& {\left({\mathrm{\nabla }}_{\mathit{x}}{\mathbf{f}}_{\mathbf{A}}\right)}^{\mathrm{T}}\mathit{d}=\mathit{d}+{\left({\mathrm{\nabla }}_x\mathit{\phi }\right)}^{\mathrm{T}}{\mathbf{G}}^{-\mathrm{T}}{\mathbf{b}}^{\mathrm{T}}\mathit{d}.\end{array}$$

To avoid computing G^−T explicitly, let us define the vector $\mathit{z}\in {\mathbb{R}}^{N_x{N}_{\mathrm{RK}}}$ such that

$$\begin{array}{}\text{(B8)}& {\mathbf{G}}^{\mathrm{T}}\mathit{z}={\mathbf{b}}^{\mathrm{T}}\mathit{d}.\end{array}$$

Because G^T is upper triangular with diagonal entries of value 1, z is the solution of a linear system easily solvable iteratively, which stands as an adjoint/dual to the RK iterative construction. Hence, we finally obtain a formula and algorithm to evaluate

$$\begin{array}{}\text{(B9)}& {\left({\mathrm{\nabla }}_{\mathit{x}}{\mathbf{f}}_{\mathbf{A}}\right)}^{\mathrm{T}}\mathit{d}=\mathit{d}+{\left({\mathrm{\nabla }}_{\mathit{x}}\mathit{\phi }\right)}^{\mathrm{T}}\mathit{z},\end{array}$$

which is key to computing Eq. (19). Indeed, Eq. (19) now reads as

$$\begin{array}{}\text{(B10a)}& {\displaystyle }\begin{array}{rl}{\mathrm{\nabla }}_{{\mathit{x}}_{\mathrm{0}}}\mathcal{J}=& -{\left({\mathrm{\nabla }}_{{\mathit{x}}_{\mathrm{0}}}{\mathbf{H}}_{\mathrm{0}}\right)}^{\mathrm{T}}{\mathit{r}}_{\mathrm{0}}^{-\mathrm{1}}{\mathit{\delta }}_{\mathrm{0}}-{\mathbf{Q}}_{\mathrm{1}}^{-\mathrm{1}}{\mathbf{\Delta }}_{\mathrm{1}}-{\left({\mathrm{\nabla }}_{{\mathit{x}}_{\mathrm{0}}}\mathit{\phi }\right)}^{\mathrm{T}}{\mathit{z}}_{\mathrm{0}}\\ & -{\mathrm{\nabla }}_{{\mathit{x}}_{\mathrm{0}}}\ln p\left({\mathit{x}}_{\mathrm{0}}\right|\mathbf{A}),\end{array}\text{(B10b)}& {\displaystyle }\begin{array}{rl}{\mathrm{\nabla }}_{{\mathit{x}}_k}\mathcal{J}=& -{\left({\mathrm{\nabla }}_{{\mathit{x}}_k}{\mathbf{H}}_k\right)}^{\mathrm{T}}{\mathit{r}}_k^{-\mathrm{1}}{\mathit{\delta }}_k-{\mathbf{Q}}_{k+\mathrm{1}}^{-\mathrm{1}}{\mathbf{\Delta }}_{k+\mathrm{1}}-{\left({\mathrm{\nabla }}_{{\mathit{x}}_k}\mathit{\phi }\right)}^{\mathrm{T}}{\mathit{z}}_k\\ & +{\mathbf{Q}}_k^{-\mathrm{1}}{\mathbf{\Delta }}_k,\mathrm{for}\mathrm{1}\le k\le K-\mathrm{1},\end{array}\text{(B10c)}& {\displaystyle }{\mathrm{\nabla }}_{{\mathit{x}}_K}\mathcal{J}=-{\left({\mathrm{\nabla }}_{{\mathit{x}}_K}{\mathbf{H}}_K\right)}^{\mathrm{T}}{\mathit{r}}_K^{-\mathrm{1}}{\mathit{\delta }}_K+{\mathbf{Q}}_K^{-\mathrm{1}}{\mathbf{\Delta }}_K,\end{array}$$

where z_k is the iterative solution of the system ${\mathbf{G}}_k^{\mathrm{T}}{\mathit{z}}_k={\mathbf{b}}^{\mathrm{T}}{\mathbf{Q}}_{k+\mathrm{1}}^{-\mathrm{1}}{\mathbf{\Delta }}_{k+\mathrm{1}}$ for $\mathrm{0}\le k\le K-\mathrm{1}$.

Second, let us look at the gradient of $\mathcal{J}(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K})$ with respect to A. From Eqs. (B4) and (B3), and now considering variations with respect to A, we obtain

$$\begin{array}{}\text{(B11)}& {\mathrm{\nabla }}_{\mathbf{A}}{\mathbf{f}}_{\mathbf{A}}={\mathrm{\nabla }}_{\mathbf{A}}\mathit{x}+\mathbf{b}{\mathrm{\nabla }}_{\mathbf{A}}\mathit{\kappa }={\mathbf{bG}}^{-\mathrm{1}}{\mathrm{\nabla }}_{\mathbf{A}}\mathit{\phi },\end{array}$$

which yields, using z as defined by Eq. (B8),

$$\begin{array}{}\text{(B12)}& {\mathit{d}}^{\mathrm{T}}\left({\mathrm{\nabla }}_{\mathbf{A}}{\mathbf{f}}_{\mathbf{A}}\right)={\mathit{d}}^{\mathrm{T}}{\mathbf{bG}}^{-\mathrm{1}}\left({\mathrm{\nabla }}_{\mathbf{A}}\mathit{\phi }\right)={\mathit{z}}^{\mathrm{T}}\left({\mathrm{\nabla }}_{\mathbf{A}}\mathit{\phi }\right).\end{array}$$

For each $\mathrm{0}\le i<N_{\mathrm{RK}}$, let us introduce ${\mathit{r}}_i=\mathit{r}\left({\mathbf{x}}_{\mathbf{i}}\right)\in {\mathbb{R}}^{N_p}$, and let us denote ${\mathit{z}}_i\in {\mathbb{R}}^{N_x}$ the subvector of z for the ith block of the Runge–Kutta scheme. Then we have, for $\mathrm{0}\le n<N_x$ and $\mathrm{0}\le p<N_p$,

$$\begin{array}{}\text{(B13)}& \begin{array}{rl}{\displaystyle }{\left[{\mathit{z}}^{\mathrm{T}}\left({\mathrm{\nabla }}_{\mathbf{A}}\mathit{\phi }\right)\right]}_{n,p}& {\displaystyle }={\sum }_{m=\mathrm{0}}^{N_x-\mathrm{1}}{\sum }_{i=\mathrm{0}}^{N_{\mathrm{RK}}-\mathrm{1}}\left[{\mathit{z}}_i{]}_m{\displaystyle \frac{\partial }{\partial A_{n,p}}}{\sum }_{q=\mathrm{0}}^{N_p-\mathrm{1}}{A}_{m,q}\right[{\mathit{r}}_i{]}_q\\ {\displaystyle }& {\displaystyle }={\sum }_{m=\mathrm{0}}^{N_x-\mathrm{1}}{\sum }_{i=\mathrm{0}}^{N_{\mathrm{RK}}-\mathrm{1}}{\sum }_{q=\mathrm{0}}^{N_p-\mathrm{1}}\left[{\mathit{z}}_i{]}_m{\mathit{\delta }}_{m,n}{\mathit{\delta }}_{p,q}\right[{\mathit{r}}_i{]}_q\\ {\displaystyle }& {\displaystyle }={\sum }_{i=\mathrm{0}}^{N_{\mathrm{RK}}-\mathrm{1}}\left[{\mathit{z}}_i{]}_n\right[{\mathit{r}}_i{]}_p={\sum }_{i=\mathrm{0}}^{N_{\mathrm{RK}}-\mathrm{1}}{\mathit{z}}_i{\mathit{r}}_i^{\mathrm{T}}.\end{array}\end{array}$$

This is key to efficiently computing Eq. (20), which now reads as

$$\begin{array}{}\text{(B14)}& {\mathrm{\nabla }}_{\mathbf{A}}\mathcal{J}=-\sum _{k=\mathrm{1}}^K\sum _{i=\mathrm{0}}^{N_{\mathrm{RK}}-\mathrm{1}}{\mathit{z}}_{k,i}{\mathit{r}}_{k,i}^{\mathrm{T}}-{\mathrm{\nabla }}_{\mathbf{A}}\ln p\left(\mathbf{A}\right),\end{array}$$

where z_k is the solution of ${\mathbf{G}}_k^{\mathrm{T}}{\mathit{z}}_k={\mathbf{b}}^{\mathrm{T}}{\mathbf{Q}}_k^{-\mathrm{1}}{\mathit{\delta }}_k$. The index k of G_k indicates that the operators defined in the entries of G are evaluated at x_k.

B3 Composition of integration steps

We now consider a resolvent which is the composition of $N_{\mathrm{c}}^k\ge \mathrm{2}$ integration steps over $[t_k,t_{k+\mathrm{1}}]$: ${\mathit{x}}^{\prime }={\mathbf{f}}_{\mathbf{A}}^{N_{\mathrm{c}}^k}\left(\mathit{x}\right)$, where x is an alias to x_k. Let us first look at the gradient with respect to the state variable. Within the scope of this section, we define x₀≡x and for $\mathrm{1}\le l\le N_{\mathrm{c}}^k$: ${\mathit{x}}_l\equiv {\mathbf{f}}_{\mathbf{A}}\left({\mathit{x}}_{l-\mathrm{1}}\right)$. Hence, ${\mathit{x}}^{\prime }={\mathit{x}}_{N_{\mathrm{c}}}$. We also define ${\mathrm{\nabla }}_{{\mathit{x}}_l}{\mathbf{f}}_{\mathbf{A}}$ as the tangent linear operator of f_A at x_l. By the Leibniz rule, we obtain

$$\begin{array}{}\text{(B15)}& {\left({\mathrm{\nabla }}_{\mathit{x}}{\mathbf{F}}_{\mathbf{A}}^k\right)}^{\mathrm{T}}=\left({\mathrm{\nabla }}_{{\mathit{x}}_{\mathrm{0}}}{\mathbf{f}}_{\mathbf{A}}{)}^{\mathrm{T}}\right({\mathrm{\nabla }}_{{\mathit{x}}_{\mathrm{1}}}{\mathbf{f}}_{\mathbf{A}}{)}^{\mathrm{T}}\mathrm{\cdots }({\mathrm{\nabla }}_{{\mathit{x}}_{N_{\mathrm{c}}-\mathrm{1}}}{\mathbf{f}}_{\mathbf{A}}{)}^{\mathrm{T}}.\end{array}$$

We can now apply Eq. (B9) to each individual integration step and obtain for any $\mathit{d}\in {\mathbb{R}}^{N_x}$

$$\begin{array}{}\text{(B16)}& ({\mathrm{\nabla }}_{{\mathit{x}}_l}{\mathbf{f}}_{\mathbf{A}}{)}^{\mathrm{T}}\mathit{d}=\mathit{d}+{\left({\mathrm{\nabla }}_{{\mathit{x}}_l}\mathit{\phi }\right)}^{\mathrm{T}}{\mathit{z}}_l,\end{array}$$

where z_l is the solution of

$$\begin{array}{}\text{(B17)}& {\mathbf{G}}_l^{\mathrm{T}}{\mathit{z}}_l={\mathbf{b}}^{\mathrm{T}}\mathit{d}.\end{array}$$

Hence, to compute ${\left({\mathrm{\nabla }}_{\mathit{x}}{\mathbf{F}}_{\mathbf{A}}^k\right)}^{\mathrm{T}}\cdot \mathit{d}$, we define ${\stackrel{\mathrm{̃}}{\mathit{x}}}_{N_{\mathrm{c}}}=\mathit{d}$ and for $N_{\mathrm{c}}-\mathrm{1}\ge l\ge \mathrm{0}$: ${\stackrel{\mathrm{̃}}{\mathit{x}}}_l=({\mathrm{\nabla }}_{{\mathit{x}}_l}{\mathbf{f}}_{\mathbf{A}}{)}^{\mathrm{T}}{\stackrel{\mathrm{̃}}{\mathit{x}}}_{l+\mathrm{1}}$. This finally reads as

$$\begin{array}{}\text{(B18)}& {\stackrel{\mathrm{̃}}{\mathit{x}}}_l={\stackrel{\mathrm{̃}}{\mathit{x}}}_{l+\mathrm{1}}+{\left({\mathrm{\nabla }}_{{\mathit{x}}_l}{\mathit{\phi }}_l\right)}^{\mathrm{T}}{\mathit{z}}_l,\end{array}$$

for $N_{\mathrm{c}}-\mathrm{1}\ge l\ge \mathrm{0}$, where z_l is the solution of

$$\begin{array}{}\text{(B19)}& {\mathbf{G}}_l^{\mathrm{T}}{\mathit{z}}_l={\mathbf{b}}^{\mathrm{T}}{\stackrel{\mathrm{̃}}{\mathit{x}}}_{l+\mathrm{1}}.\end{array}$$

To compute the key terms in the gradients Eq. (19), d must be chosen to be ${\mathbf{Q}}_{k+\mathrm{1}}^{-\mathrm{1}}{\mathbf{\Delta }}_{k+\mathrm{1}}$ where $\mathrm{0}\le k\le K-\mathrm{1}$ and

$$\begin{array}{}\text{(B20)}& {\left({\mathrm{\nabla }}_{\mathit{x}}{\mathbf{F}}_{\mathbf{A}}^k\right)}^{\mathrm{T}}{\mathbf{Q}}_{k+\mathrm{1}}^{-\mathrm{1}}{\mathbf{\Delta }}_{k+\mathrm{1}}={\stackrel{\mathrm{̃}}{\mathit{x}}}_{\mathrm{0}}.\end{array}$$

Second, we look at the gradient with respect to A. In this case, the application of the Leibniz rule yields

$$\begin{array}{}\text{(B21)}& \begin{array}{rl}{\mathrm{\nabla }}_{\mathbf{A}}{\mathbf{F}}_{\mathbf{A}}^k& =\sum _{l=\mathrm{0}}^{N_{\mathrm{c}}-\mathrm{1}}\left({\mathrm{\nabla }}_{{\mathit{x}}_{N_{\mathrm{c}}-\mathrm{1}}}{\mathbf{f}}_{\mathbf{A}}\right)\mathrm{\cdots }\left({\mathrm{\nabla }}_{{\mathit{x}}_{l+\mathrm{1}}}{\mathbf{f}}_{\mathbf{A}}\right){\mathrm{\nabla }}_{\mathbf{A}}{\mathbf{f}}_{\mathbf{A}}\left({\mathit{x}}_l\right)\\ & =\sum _{l=\mathrm{0}}^{N_{\mathrm{c}}-\mathrm{1}}\left({\mathrm{\nabla }}_{{\mathit{x}}_{l+\mathrm{1}}}{\mathbf{f}}_{\mathbf{A}}^{N_{\mathrm{c}}-l-\mathrm{1}}\right){\mathrm{\nabla }}_{\mathbf{A}}{\mathbf{f}}_{\mathbf{A}}\left({\mathit{x}}_l\right),\end{array}\end{array}$$

where ${\mathrm{\nabla }}_{{\mathit{x}}_{l+\mathrm{1}}}{\mathbf{f}}_{\mathbf{A}}^{N_{\mathrm{c}}-l-\mathrm{1}}=\left({\mathrm{\nabla }}_{{\mathit{x}}_{N_{\mathrm{c}}-\mathrm{1}}}{\mathbf{f}}_{\mathbf{A}}\right)\mathrm{\cdots }\left({\mathrm{\nabla }}_{{\mathit{x}}_{l+\mathrm{1}}}{\mathbf{f}}_{\mathbf{A}}\right)$. But ∇_Af_A(x_l), which focuses on a single integration step, is given by Eq. (B11),

$$\begin{array}{}\text{(B22)}& {\mathrm{\nabla }}_{\mathbf{A}}{\mathbf{f}}_{\mathbf{A}}\left({\mathit{x}}_l\right)={\mathbf{bG}}_l^{-\mathrm{1}}{\mathrm{\nabla }}_{\mathbf{A}}{\mathit{\phi }}_l\end{array}$$

and from Eq. (B12),

$$\begin{array}{}\text{(B23)}& {\mathit{d}}^{\mathrm{T}}{\mathrm{\nabla }}_{\mathbf{A}}{\mathbf{f}}_{\mathbf{A}}\left({\mathit{x}}_l\right)={\mathit{z}}_l^{\mathrm{T}}\left({\mathrm{\nabla }}_{\mathbf{A}}{\mathit{\phi }}_l\right).\end{array}$$

As a result, we obtain

$$\begin{array}{}\text{(B24)}& {\mathrm{\nabla }}_{\mathbf{A}}\mathcal{J}=-\sum _{l=\mathrm{0}}^{N_{\mathrm{c}}-\mathrm{1}}\sum _{k=\mathrm{1}}^K\sum _{i=\mathrm{0}}^{N_{\mathrm{RK}}-\mathrm{1}}{\mathit{z}}_{k,l,i}{\mathit{r}}_{k,l,i}^{\mathrm{T}}-{\mathrm{\nabla }}_{\mathbf{A}}\ln p\left(\mathbf{A}\right),\end{array}$$

where z_k,l is the solution of

$$\begin{array}{}\text{(B25)}& {\mathbf{G}}_{k,l}^{\mathrm{T}}{\mathit{z}}_{k,l}={\mathbf{b}}^{\mathrm{T}}{\left({\mathrm{\nabla }}_{{\mathit{x}}_{l+\mathrm{1}}}{\mathbf{f}}_{\mathbf{A}}^{N_{\mathrm{c}}-l-\mathrm{1}}\right)}^{\mathrm{T}}{\mathbf{Q}}_k^{-\mathrm{1}}{\mathit{\delta }}_k.\end{array}$$

All of these results, Eqs. (B10), (B14), (B20), and (B24), allow us to efficiently compute the gradients of the cost function $\mathcal{J}(\mathbf{A},{\mathit{x}}_{\mathrm{0}:K})$ with respect to both A and x_0:K. Note, however, that they have been derived under the simplifying assumption that ϕ_A is given by Eq. (2) with a traditional matrix multiplication between A and r(x), but not by the compact Eq. (8). When relying on homogeneity and/or locality, the calculation of the gradient with respect to A follows the principle described above but requires further adaptations, which can be derived using Eq. (A2), with the asset of strongly reducing the computational burden.

Appendix C: Adjoint differentiation with PyTorch and TensorFlow

As an alternative to the explicit computation of the gradients of Eq. (17) and the associated adjoint models, we have used PyTorch and TensorFlow as automatic differentiation tools. Only the cost function code needs to be implemented. We made a few tests of the experiments of Sect. 4 that showed that the fastest code is a C++ implementation using the explicit gradients, followed by an implementation using Python/Numpy/Numba using the explicit gradients, followed by a much slower implementation with TensorFlow (graph execution), followed by an implementation with TensorFlow (eager execution) and finally with PyTorch. Our experiments made use of a multi-core CPU and/or a GPU. This purely qualitative ranking is not surprising since (i) PyTorch and TensorFlow excel in tensor algebra operations which are not massively used in the way we built our cost function with relatively few but significant parameters, and (ii) the time spent in the development of each approach scales with their speed.