Simple statistics for complex Earthquake time distributions

Here we investigated a statistical feature of earthquake time distributions in the southern California earthquake catalog. As a main data analysis tool, we used a simple statistical approach based on the calculation of integral deviation times (IDT) from the time distribution of regular markers. The research objective is to define whether and when the process of earthquake time distribution approaches to randomness. Effectiveness of the IDT calculation method was tested on the set of simulated color noise data sets with the different extent of regularity, as well as for Poisson process data sets. Standard methods of complex data analysis have also been used, such as power spectrum regression, Lempel and Ziv complexity, and recurrence quantification analysis, as well as multiscale entropy calculations. After testing the IDT calculation method for simulated model data sets, we have analyzed the variation in the extent of regularity in the southern California earthquake catalog. Analysis was carried out for different periods and at different magnitude thresholds. It was found that the extent of the order in earthquake time distributions is fluctuating over the catalog. Particularly, we show that in most cases, the process of earthquake time distributions is less random in periods of strong earthquake occurrence compared to periods with relatively decreased local seismic activity. Also, we noticed that the strongest earthquakes occur in periods when IDT values increase.

1 Introduction

Time distributions of earthquakes remains one of the important questions in present-day geophysics. Nowadays, the results of theoretical research and the analysis of features of earthquake temporal distributions from different seismic regions with different tectonic regimes carried out worldwide can be found in Matcharashvili et al. (2000), Telesca et al. (2001, 2012), Corral (2004), Davidsen and Goltz (2004), Martínez et al. (2005), Lennartz et al. (2008), and Chelidze and Matcharashvili (2007).

Such analyses, among others, often aim at the assessment of the strength of correlations or the extent of the determinism and/or regularity in the earthquake time distributions. One of the main conclusions of such analyses is that earthquake generation, in general, does not follow the patterns of a random process. Specifically, well established clustering, at least in time (and spatial domains), suggests that earthquakes are not completely independent and that seismicity is characterized by slowly decaying correlations (named long-range correlations); such behavior is commonly exhibited by nonlinear dynamical systems far from equilibrium (Peng et al., 1994, 1995). Moreover, it was shown that in the temporal and spatial domains, earthquake distributions may reveal some features of a low-dimensional, nonlinear structure, while in the energy domain (magnitude distribution) distributions are close to a random-like, high-dimensional process (Goltz, 1998; Matcharashvili et al., 2000). Moreover, according to present views, the extent of regularity of the seismic process should vary in time and space (Goltz, 1998; Matcharashvili et al., 2000, 2002; Abe and Suzuki, 2004; Chelidze and Matcharashvili, 2007; Iliopoulos et al., 2012).

At the same time, the details of how the extent of randomness (or non-randomness) of seismic processes change over time and space still remain unclear. In the present work, on the basis of the southern California earthquake catalog, we aimed to focus on this question and analyzed earthquake time distributions to find where they are closer to randomness.

Figure 1 Explanation of the used approach. Triangles – time location of original earthquakes (T_EQ(i)), circles – time location of regular markers (T_R(i)). DT_(i) denotes the difference between the time of earthquake occurrence (T_EQ(i)) in the catalog and the time point of the regular marker (T_R(i)).

2 Data and methods

Our analysis is based on the southern California earthquake catalog available from http://www.isc.ac.uk/iscbulletin/search/catalogue/ (last access: 5 July 2018). As far as we aimed to analyze temporal features of original earthquake generation, we tried to have a long as possible period of observation with a low-as-possible representative threshold. For this purpose, according to results of time completeness analysis (not shown here), we decided to focus on the time period from 1975 to 2017 since in the middle of the 1970s of the last century the magnitude of completeness clearly decreased. The southern California (SC) earthquake catalog for the considered period is complete for M=2.6, according to the Gutenberg–Richter relationship analysis.

In general, we are presently developing an approach aiming to discern features of the complex data sets (in this case earthquake, EQ, time distribution) by comparing them with data sets with the predefined dynamical structures. In the present work, in the frame of this general idea, we started from the simplest case, comparing the natural time distribution of earthquakes in SC catalog with the time distribution of regular markers, according to the scheme shown in Fig. 1.

Particularly, knowing the duration of the whole period of observation in the considered catalog (22 167 178 min, from 1 January 1975 to 23 February 2017) and the number of earthquakes (34 020) with the magnitude above a representative threshold (M=2.6), we calculated the time step between consecutive regular markers (651.6 min), which in fact is the mean time of earthquake occurrence for the considered period. Then, for each earthquake in the catalog, we calculated the difference between original event occurrence time and the time point of the regular marker. We denoted DT(i) as the time interval (delay or deviation time) between occurrence of the original earthquake T_EQ(i) and corresponding ith regular marker T_R(i). It is clear that the original earthquake (EQ_i) may occur prior to or after the corresponding regular marker (R_i), so by DT_(i) with minus or plus sign we understand that earthquakes occurred prior to or after regular markers accordingly. More generally, we speak about differences (deviations) between observed waiting times x(i) and mean occurrence time $\stackrel{\mathrm{‾}}{x}$ over the considered period. It is clear that the character of evolution of these deviations should be closely related with the character of the considered process, here earthquake time distributions. Thus, alternatively to the above-mentioned text, integral deviation times (IDTs) can be calculated as cumulative sums of deviations. In any case, IDT will depend on the time span of the analyzed period (or the sum of waiting times, as well as on the number of waiting time data, n. Therefore, we calculated norm IDT values for the window span and number of data in analyzed window. It is expected that when n→∞, IDT will approach zero. Logically, for a random sequence, the sum of the deviation times should approach zero faster compared to less random ones. This is the main assumption of the present analysis. From this point of view, the approach looks close to the cumulative sums (Cusum) test, where for a random sequence, the sum of excursions of the random walk should be near zero (Rukhin et al., 2010).

Prior to using it for the seismic process, we needed to fulfill empirical testing of the idea behind the IDT calculation procedure. Specifically, we aimed to test whether the IDT calculation can be sensitive to dynamical changes occurring in complex data sets with known dynamical structures. We started from the analysis of model data sets with a different extent of randomness. Specifically, we used simulated noise data sets of different color with a power spectrum function (1∕f^β), where the scale exponent (β) varied from about 0 to 2. These noises, according to generation principles, logically have to be different, but for purposes of our analysis we needed to have strong quantitative assessments of such differences. This is why at first, these noise data sets have been investigated by several data analysis methods, often used to assess different aspects of changes occurring in dynamical processes of interest. Specifically, power spectrum regression, Lempel and Ziv algorithmic complexity calculation, as well as recurrence quantification analysis and multiscale entropy calculation methods have been used for simulated model data sets. All these popular methods of time series analysis are well described in a number of research articles and we will just briefly mention their main principles.

Power spectrum regression exponent calculation enables us to elucidate scaling features of data set in the frequency domain. By this method, a fractal property is reflected as a power law dependence between the spectral power (S(f)) and the frequency (f) by spectral exponent β:

$$\begin{array}{}\text{(1)}& S\left(f\right)\sim {\displaystyle \frac{\mathrm{1}}{f^{\mathit{\beta }}}},\end{array}$$

where β is often regarded as a measure of the strength of the persistence or anti-persistence in data sets. As easily calculated from the log–log power spectrum plot, β is related to the type of correlations present in the time series (Malamud and Turcotte, 1999; Munoz-Diosdado et al., 2005; Stadnitski, 2012). For example, β=0 corresponds to the uncorrelated white noise, and processes with some extent of memory or long-range correlations are characterized by nonzero values of spectral exponents.

Next, we proceeded to the Lempel and Ziv algorithmic complexity (LZC) calculation (Lempel and Ziv, 1976; Aboy et al., 2006; Hu et al., 2006), which is a common method for quantification of the extent of order (or randomness) in data sets of different origins. LZC is based on the transformation of an analyzed sequence into a new symbolic sequence. For this, original data are converted into a 0, 1, sequence by comparing to a certain threshold value (usually median of the original data set). Once the symbolic sequence is obtained, it is parsed to obtain distinct words, and the words are encoded. Denoting the length of the encoded sequence for those words, the LZC can be defined as

$$\begin{array}{}\text{(2)}& C_{\mathrm{LZ}}={\displaystyle \frac{L\left(n\right)}{n}},\end{array}$$

where L(n) is the length of the encoded sequence and n is the total length of the sequence (Hu et al., 2006). Parsing methods can be different (Cover and Thomas, 1991; Hu et al., 2006). In this work, we used the scheme described in Hu et al. (2006).

Next, in order to further quantify changes in the dynamical structure of simulated data sets, we have used the recurrence quantification analysis (RQA) approach (Zbilut and Webber, 1992; Webber and Zbilut, 1994; Marwan et al., 2007). RQA is often used for analysis of different types of data sets and represents a quantitative extension of the recurrent plot construction method. The recurrent plot itself is based on the fact that returns (recurrence) to the certain condition of the system (or state space location) is a fundamental property of any dynamical system with quantifiable extent of determinism in underlying laws (Eckman et al., 1987). In order to successfully fulfill RQA calculations, the phase space trajectory should be reconstructed from the given scalar data sets at first. It is important to test the proximity of points of the phase trajectory by the condition that the distance between them is less than a specified threshold ε (Eckman et al., 1987). In this way, we obtain a two-dimensional representation of the recurrence features of dynamics, which is embedded in a high-dimensional phase space. Then, a small-scale structure of recurrent plots can be quantified (Zbilut and Webber, 1992; Webber and Zbilut, 1994, 2005; Marwan et al., 2007; Webber et al., 2009; Webber and Marwan, 2015). Particularly, the RQA method enables us to quantify features of a distance matrix of recurrence plot, by means of several measures of complexity. These measures of complexity are based on the quantification of diagonally and vertically oriented lines in the recurrence plot. In this research, we calculated one such measure: the percent determinism (%DET) which is defined as the fraction of recurrence points that form diagonal lines of recurrence plots and which shows changes in the extent of determinism in the analyzed data sets.

An additional test, which we used to quantify the extent of regularity in the modeled data sets, is the composite multiscale entropy (CMSE) calculation (Wu et al., 2013a). The CMSE method represents expansion of the multiscale entropy (MSE) (Costa et al., 2015) method, which in turn originates from the concept of sample entropy (SampEn; Richman and Moorman, 2000). SampEn is regarded as an estimator of complexity of data sets for a single timescale. In order to capture the long-term structures in the time series, Costa et al. (2015) proposed the above-mentioned MSE algorithm, which uses SampEn of a time series at multiple scales. At the first step of this algorithm, often used in different fields, a coarse-graining procedure is used to derive the representations of a system's dynamics at different timescales; at the next step, the SampEn algorithm is used to quantify the regularity of a coarse-grained time series at each timescale factor. The main problem of MSE is that, for a shorter time series, the variance in the entropy estimator grows very fast as the number of data points is reduced. In order to avoid this problem and reduce the variance of estimated entropy values at large scales, the method of the CMSE calculation was developed by Wu and colleagues (Wu et al., 2013a).

Figure 2 Typical plot of the power spectrum of simulated data sets with different spectral regressions, (a) β=0.001 and (b) β=1.655.

3 Results and discussion

3.1 Analysis of model data sets

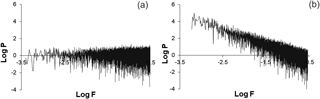
As we mentioned in the previous section, we first need to ascertain whether calculation of IDT values is sensitive to dynamical changes occurring in analyzed data sets. To this end, we decided to generate artificial data sets of one and the same type; for example, noises, which according to the generation procedure should be measurably different in the frequency content, representing different types of color noises. We have started from the analysis of 34 020 data length sequences of these noise data sets. For clarity, we add here that to test the robustness of results, the same analyses were performed on much longer data sets, but here we show results for simulated noise data sets, which are of the same length as the original data sets from the used seismic catalogue. The noise data sets have been generated according to concepts described in Kasdin (1995), Milotti (2007), and Beran et al. (2013). As metrics for these data sets we have used the above-mentioned power spectrum exponents (β), also referred to as the spectral indexes (Schaefer et al., 2014). Specifically, we have analyzed seven such data sets having the following spectral exponents: 0.001, 0.275, 0.545, 0.810, 1.120, 1.387, and 1.655. Values of β are often used as a metric for the fractal characteristics of data sequences (Shlesinger, 1987; Schaefer et al., 2014). In our case, different spectrum exponents of simulated noise data sets indicate that they are different by the extent of correlations in the frequency content (Schaefer et al., 2014). Indeed, the first noise set, with β=0.001 (Fig. 2a) was closest to the white noise and the last one, with β=1.655 (Fig. 2b), manifested the features closer to colored noises of red or Brownian type, with detectable dynamic structure. In addition to this, taking into account that we aimed to analyze seismic data sets, we regarded it logical to also consider the random process, which is often used by seismologists – a Poisson process. We generated the set of 34 020 data-long sequences of the Poisson process. It was quite expected that the spectral exponent of such sequences is close to that of white noise.

Figure 3 LZC and %DET values calculated for seven noise data sets with different spectral indexes.

For further analysis, in order to differentiate simulated (noise and Poisson process) data sets by the extent of randomness, we used algorithmic complexity (LZC) and recurrence quantification analysis methods, as well as testing based on MSE analysis.

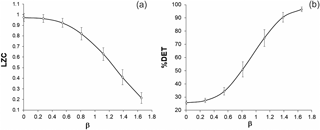
In Fig. 3, we show results of LZC and %DET calculations; particularly presented here are averages of values calculated for consecutive 1000 data windows shifted by 100 data. Both methods, though based on different principles, help to answer the question of how similar or dissimilar the considered data sets are by the extent of randomness. We see that the Lempel and Ziv complexity measure decreases from 0.98 to 0.21 when β of noises increases. This means that the extent of regularity in simulated data sets increases. The same conclusion is drawn from RQA: the percentage of determinism increases from 25 to 96.5 when the spectral exponent increases. For both LZC and RQA measures, differences in compared neighbor groups in figures are statistically significant at p=0.01. Thus, according to Fig. 3, the extent of regularity in simulated noise sequences clearly increases from close to white (β=0.001) to close to Brownian (β=1.655) noise. For the Poisson process data sequences, the LZC measure reaches 0.97–0.98 and %DET is in the range 25–26, i.e., these values are close to what we obtain for white noise.

Thus, the results of LZC and %DET calculations confirm the result of power spectrum exponent calculations, and show that considered color noise data sets are different from white noise and the Poisson process by the extent of regularity.

Additional multiscale, CMSE, analysis also shows (Fig. 4) that the extent of regularity in model noise data sets increases, when they become “more” colored (from β=0.001 to β=1.655). We see that for small scales (exactly for scale one and partly scale two), noise data sets reveal decreases in the entropy values for simulated data sets, when spectral indexes rise from β=0.001 to β=1.655. This is logical for simulated data sets, where the extent of order, according to the above analysis, should slightly increase. At the same time, while at larger scales, the value of entropy for the noise data set with β=0.001 continues to monotonically decrease like for the coarse-grained white noise time series (Costa et al., 2015). On the other hand, the value of entropy for 1∕f type processes with the β values close to pink noise (0.81, 1.12) remained almost constant for all scales. As noticed by Costa et al. (2015), this fact was confirmed in different articles on multiscale entropy calculation (see e.g., Chou, 2012; Wu et al., 2013a, b). Costa and coauthors explained this result by the presence of complex structures across multiple scales for 1∕f type of noises. From this point of view, in a color noise set closer to a Brownian-type process, the emerging complex dynamical structures should become more and more organized. Apparently, these structures are preserved over multiple scales including small ones. This is clearly indicated by the gradual decrease in calculated values of entropy for sequences with β=1.12 to β=1.387 and β=1.654 at all considered scales (see Fig. 4). Poisson process data sets (not shown in figure) in the sense of results of multiscale analysis are close to a white noise sequence with β=0.001.

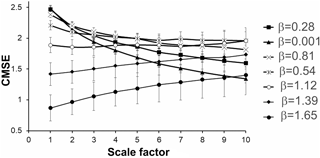
Figure 4 CMSE values versus scale factor for simulated data sequences with different spectral indexes.

Thus, CMSE analysis additionally confirms that the complex model data sets used in this research are characterized by quantifiable dynamical differences.

Once we had data sets with quantifiable differences in their dynamical structures, we started to test the ability of the IDT calculation to detect these differences.

For this, we created cumulative sum sequences of seven noise data sets and data sets of the Poisson process and regarded them as models of time occurrences of consecutive events. We treated these, 34 020 data-long, sets for time occurrence sequence of real earthquakes and calculated IDT values for different windows. Taking into consideration that cumulative sum (or time span in the case of seismic catalog) of windows may be different (excluding the case when data sets have been specially generated so that the cumulative sum is equal) we obtained normed IDT values to the span of window and the number of data. Results of the calculation are presented in the lower curve (circles) in Fig. 5a. Here also we present results of similar calculations on the same data sets performed for shorter windows (see squares, triangles, and diamonds in Fig. 5a).

As we see, absolute values of IDTs normed to window span and number of data, calculated for the model data sets, indicate stronger deviation from zero, when the extent of order in simulated noise data sets increases (according to the above analysis). Average values of IDTs calculated for data sets with spectral exponents closer to Brownian noise significantly differ from white noise at p=0.01 (Fig. 5a). It needs to be pointed out that compared to results obtained by the above-mentioned methods, IDT calculation looks even more sensitive to slight dynamical changes occurring in simulated data sets; note the more than 1.5 difference between sequences with β=0.001 and β=1.654 for the entire length of data sets (circles in Fig. 5a). It is also quite logical that the longer the length of considered the window, the closer to zero the corresponding IDT value in Fig. 5 is.

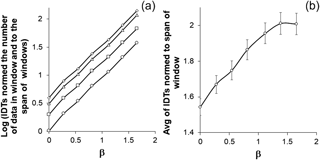
Figure 5 (a) Logarithms of, normed to the span of window, absolute values of IDT calculated for different lengths (circles – 34 020, squares – 20 000, triangles – 10 000, diamonds – 5000 data) of windows of simulated noise data sets with different spectral indexes. (b) Averages of IDT values calculated for 100 data windows normed to the span of window simulated noise data sets with different spectral indexes.

It needs to be pointed out that according to IDT calculations, the Poisson process looks more random than white noise. Indeed, logarithms of normed to window span IDT values calculated for random Poisson process data sets were lower than for white noise (not shown in figures). For further analysis, it is important to mention that comparing data sets with different extent of order, we see that the drawn conclusions do not practically depend on the length of used data sets. No less important is that, as it is shown in Fig. 5b, differences found for longer windows are preserved for the short, 100 data-long sequences. For 100 data windows, the difference between white noise, as well as the Poisson process, data sets and colored noises is statistically significant at p=0.01. Taking into consideration the importance of results of IDT calculations for short (100 data) windows, we additionally present reconstructed PDF curves fitted to the normal distribution according to real calculations (different markers in Fig. 6). From this figure, we see that the portion of IDT values which are closer to zero increase, when the extent of order in the data sets decrease. Besides, it also becomes clear that even for short data sets IDT calculation is useful to detect differences in considered data sets (in this case norming to the number of data in the window is not necessary because all windows contain the same number of data).

Thus, based on the analysis of specially simulated data sequences we conclude that the IDT calculation method is effective in detecting small changes occurring in, even short, complex data sets with different dynamical structures.

3.2 Analysis of earthquake time distributions in the southern California catalog

In this section we proceeded to the analysis of original data sets drawn from the southern California seismic catalog using the IDT calculation approach.

As it was proposed above, for random sequences compared to more regular data sets, the sum of the deviation times should approach zero faster in the infinite length limit. Results presented in the previous section confirms this in the example of model random (or random-like) data sets with different extent of regularity (or randomness).

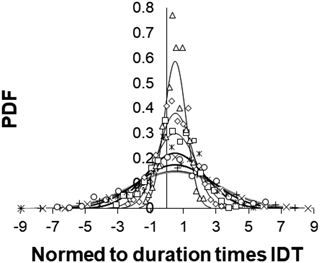
Figure 6 PDF of, normed to window length, IDT values calculated for consecutive 100 data windows of simulated noise data sequences, shifted by 100 data. From top to bottom, black curves correspond to β=0.001 (triangles), β=0.275 (diamonds), β=0.545 (squares), β=0.810 (asterisks), β=1.120 (circles), β=1.387 (plus signs), and the grey curve corresponds to β=1.655 (cross signs).

In the case of a real earthquake generation process, which according to present views can not be regarded as completely random (Goltz, 1998; Matcharashvili et al., 2000, 2016; Abe and Suzuki, 2004; Iliopoulos et al., 2012), we should assume that the IDTs for the periods with the more random-like earthquake time distributions will be closer to zero, compared to the less random ones.

To show this, we used the seismic catalog of southern California, the most trustworthy database for analysis targeted in this research. Aiming at the analysis of temporal features of seismic process, we intentionally avoided any cleaning or filtering of the catalog in order to preserve its original temporal structure. Therefore, according to common practice (see e.g., Christensen et al., 2002; Corral, 2004) we regard the seismic processes in this catalog as a whole, irrespective of the details of tectonic features, earthquake location, or their classification as mainshocks or aftershocks.

It was quite understandable that, for such a catalog, we logically should expect time clustering of interdependent events: foreshocks and aftershocks. This, in the context of our analysis, apparently could lead to a considerable amount of events occurring prior to corresponding regular markers (probably mostly aftershocks). Thus, it was interesting to know how the number of events occurred prior to or after regular markers and especially how the result of IDT calculations (which directly depends on the number of events that occurred prior to and after regular markers) is related with the time locations of such interdependent events.

Here we underline the fact that both IDT values as well as the portion of events that occurred prior to or after regular markers (as defined in the methods section) would strongly depend on the position and length of a certain time window in the catalog. Thus, we focused on the whole duration period of the considered catalog (at the representative threshold M=2.6). We found that in this catalog, 55 % of all earthquakes occurred prior to and 45 % after the regular time markers. To elucidate the role of dependent events on this ratio we analyzed the catalog for higher representative thresholds. At increased M=3.6 representative magnitude threshold, we found that the portion of earthquakes occurred prior to marker decrease (33 % of all earthquakes). This provided an argument in favor of the assumption that the prevalence of earthquakes, which occur prior to markers, may indeed be related with dependent low-magnitude events (supposedly mostly aftershocks). At the same time, further increase in representative threshold convinces us that dependent low-magnitude events in the catalog may not be the sole cause influencing the amount of earthquakes that occurred prior to markers. Indeed, the portion of events that occurred prior to markers increased to 42 % at the representative threshold M=4.6. Most noticeable is that at the highest considered representative threshold, M=5.6, we observe a further increase in the portion of earthquakes occurring prior to regular markers; to the level observed for M=2.6 threshold (55 % of all events). Thus, it seems unlikely that the ratio between events that occurred prior to or after regular markers may be related only with dependent events (aftershocks).

Next, we calculated IDT values for the entire observation period at different representative thresholds. It was found that IDT values calculated for the entire observation period of the southern California earthquake catalog (at representative threshold M=2.6) were −14 611 458 375 min (as mentioned above, the “minus” sign here denotes the direction of summary deviation along the time axis). We compare this value to the IDT values at larger representative thresholds. It was clear that the increase in representative threshold will essentially decrease the umber of earthquakes and also may somehow change the analyzed period of the catalog. Thus, we calculated normed IDT values to the number of earthquakes and to the time span of the catalog. Normed in this way, IDT vales are 0.021, 0.023, 0.022, and −0.030 at representative thresholds M=2.6, M=3.6, M=4.6, and M=5.6 accordingly. It was expected that the increase in the magnitude threshold will make the time distribution of remained stronger EQs more random. Indeed, calculated values of IDTs decreased when the representative threshold increased. At the same time, normalization to the time span and number of events shows that the time distribution features of stronger earthquakes, in principle, do not differ from smaller ones.

In this sense, it is logical that decreased probability of dependent events, at increased representative threshold, do not necessarily cause a proportional increase in the number of occurred after regular markers events, though absolute values of IDT drastically decrease. These results also indicate that the ratio between events, occurred prior to or after regular markers, found for the entire span of SC catalog, as well as the IDT value, should not be reduced only to the distributional features of dependent events.

Further, we needed to clear up whether the ratio of events occurred prior to or after regular markers and especially obtained IDT values, are characteristics of the time distributions of earthquakes in the SC catalog or they reflect an influence of some unknown random effects, which are not directly related with the seismic process. For this, we started to calculate IDT values for the set of randomized catalogs. In these artificial catalogs, the original time structure of the southern California earthquake distributions was destroyed prior to analysis. Specifically, occurrence times of original events have been randomly shuffled (i.e., earthquake time locations have been randomly changed over the entire time span of more than 42 years). We have generated 150 such randomized catalogs and for each of them IDT values have been calculated for the whole catalog time span (which was the same as for the original catalog).

It was found that for the whole period of observation, earthquakes prevailed in 58 % of all time-randomized catalogs, and occurred prior to the corresponding regular markers. At the same time, unlike the original catalog where 55 % of earthquakes occurred prior to corresponding regular markers, in the randomized catalogs the portion of such earthquakes, occurred prior to markers, varied in a wide range (from 51 to 92 %). Thus, in spite of some similarity to the portion of events occurred prior to and after regular markers, original and time-randomized catalogs are still different.

Next, comparing the averaged IDT value of randomized catalogs (calculated from IDTs of 150 randomly shuffled catalogs) we found that it is also with minus sign (−159 755 608 min). This was expected since in 58 % of cases of randomized catalogs, prevailed earthquakes occurred prior to regular markers. Thus, comparing the average of IDT, calculated for the entire length of randomized catalogs, with the IDT value of the original SC catalog, we see that the last one is 2 orders of magnitude larger. The difference between IDT of the whole original catalog and the average IDT of randomized catalogs was statistically significant, with Z score = 11.2, corresponding to p=0.001 (Bevington and Robinson, 2002; Sales-Pardo et al., 2007). For clarity, we add here that IDT values from each of the randomized catalogs was essentially smaller than IDT from the original catalog and thus effects of averaging cannot play any role.

The difference between IDT values calculated for original and time-randomized catalogs is further highlighted in Fig. 7, where normed to the windows span IDT values are presented. We see that in all cases normed-to-windows-span IDTs are clearly smaller than for the original catalog (6.59 × 10²). It is interesting that in at least 30 % of cases, IDTs calculated for randomized catalogs are more than 2 orders smaller than IDT for the original catalog.

From this analysis two important conclusions can be drawn: (i) IDT value, calculated for the considered period of the southern California earthquake catalog, expresses the internal time distribution features of the original seismic process, and (ii) random-like earthquake time distributions lead to lower (closer to zero) IDT values comparing to the whole original catalog.

All above results obtained for simulated data sets as well as for the time distributions of earthquakes in the original catalog undoubtedly shows that the time distribution of earthquakes in southern California for the entire period should be regarded as a strongly nonrandom process (IDT is larger than for randomly distributed in time earthquakes). Therefore, the result of this simple statistical analysis is in complete agreement with our earlier results, obtained by contemporary nonlinear data analysis methods, as well as with the results of similar analysis reported by other authors, which used different methodological approaches, see e.g., Goltz (1998), Matcharashvili et al. (2000, 2016), Abe and Suzuki (2004), Telesca et al. (2012), and Iliopoulos et al. (2012).

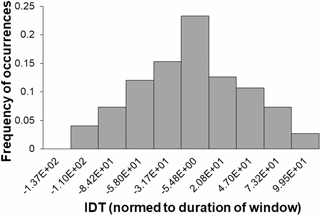
Figure 7 Frequency of occurrences of, normed to the span of window, integral deviation time values (IDTs), calculated for each of the 150 randomized catalogs for the whole period.

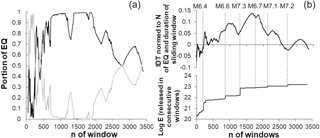
Figure 8 Calculated for extending by 10 consecutive data windows in the southern California earthquake catalog, (a) portion of earthquakes occurred prior to (grey) and after (black) regular markers in each window, (b) normed to the number of EQs and time duration of expanding windows IDTs (top), cumulative amount of released in window seismic energies (bottom).

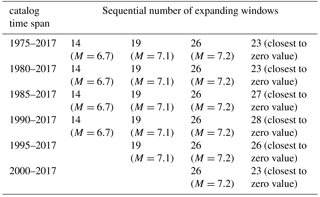
Thus, we found that for the whole period of the considered catalog, prevailed earthquakes occurred prior to corresponding regular markers (see also the last point in the upper curve of Fig. 8b). At the same time, as was also mentioned, the number of earthquakes that occurred prior to or after corresponding regular markers may change depending on the time span of the analyzed catalog. The same can be said about the values of the IDTs. In order to investigate the character of the time variation in IDT values of the SC catalog in different periods, we fulfilled calculation for the expanding time windows. Specifically, we have calculated IDT values starting from the first 100 data (earthquakes), expanding initial window by the consecutive 10 data to the end of the catalog. In Fig. 8, we see that the number and the time location of earthquakes (relative to regular markers), undergoes essential change, when the length of the analyzed part of the catalog (analyzed window's length) gradually expands to the end of the catalog (in our case from 1 January 1975 to 23 February 2017).

As it is shown in Fig. 8a, in most of the analyzed windows the majority of earthquakes occurred after regular markers, although there are windows with the opposite behavior. So far, most earthquakes in the windows occurred after regular markers, thus it is not surprising that IDTs calculated for consecutive windows are mostly positive. This is clear from Fig. 8b (upper curve), where we see windows with negative IDTs too. Thus, the values of IDTs calculated for extended windows in different periods vary in a wide range, increasing or decreasing and sometimes coming close to zero.

Here we point out again that based on results of the above analysis, accomplished for simulated data sets and randomized catalogs, we suppose that when IDT values approache zero, the dynamical features of the originally nonrandom seismic process undergoes qualitative changes and becomes random-like or at least is closer to randomness. In other cases, when IDT values change over time but are far from zero, we observe quantitative changes in the extent of regularity of nonrandom earthquake time distributions.

From this point of view it is interesting that earthquake time distributions look more random-like for the relatively quiet periods, when the amount of seismic energy calculated according to Kanamori (1997) decreased comparing to values released in the neighboring windows prior to or after the strongest earthquakes. This is noticeable in the lower curve of Fig. 8b, where we present cumulative values of seismic energy, calculated for consecutive windows, expanding by 10 events to the end of the catalog. We see that in southern California from 1975 to 2017, the strongest earthquakes never occurred in periods when the IDT curve comes close to zero or crosses the abscissa line. To avoid misunderstanding because of restricted visibility in Fig. 8b, we point out here that an M=6.4 earthquake has occurred in the window 256, from the start of the catalog, and the IDT curve crossed the abscissa later in the window 266, from the start of the catalog. Specifically, this was the nearest expanding window with the IDT value closest to zero, started 100 events later. In real time, crossing of the IDT took place in windows ending 2.5–3 h after the M=6.4 mainshock.

Results in Fig. 8 also provide interesting knowledge about the relation between IDT and the amount of released seismic energy. As we see, the three strongest earthquakes in the southern California earthquake catalog (1975–2017) occurred on the rising branch of the IDT curve close or immediately after local minima. This local decrease in IDT values, possibly, points to the decreased extent of regularity (or increased randomness) in the earthquake temporal distribution in periods prior to the strongest earthquakes in California.

Above we already discussed the influence of an increased representative threshold on the calculated IDT value for entire catalog span. Now it is necessary to check how the change of representative threshold will influence obtained results for expanding windows. This was a very important aspect of our analysis, because there is a well known point of view that the time distribution of large (considered as independent events – coupling between which is an exception rather than a rule) and medium to small earthquakes (for which time distributions may be governed or triggered by the interaction between events) are significantly different (Lombardi and Marzocchi, 2007).

To see how the results of the IDT analysis may be influenced by considering smaller or stronger earthquakes, we carried out analysis of the southern California catalog for earthquakes above M=3.6 and M=4.6 thresholds. Analysis has been accomplished (see results in Figs. 10 and 11) in a manner, similar to the scheme for threshold M=2.6, i.e., for the entire available period 1975–2017 (e.g., in Fig. 9).

For better visibility of changes in the process of energy release in Figs. 10 and 11 (also in Fig. 9, bottom), we show increments of seismic energy release only calculated for the last 10 events in each consecutive window, opposite to Fig. 8 where we presented energies released by all earthquakes in each window. This was done to make the fine structure of changes in energy release in the expanding (by consecutive 10 events) part of windows more visible, which otherwise is hidden by the strong background level of the summary energy release in the whole window. At the same time, we should not forget that IDTs in Figs. 9–11 are calculated for the entire length of windows and that real evolution of energy release looks similar to that presented in Fig. 8b.

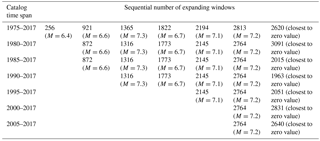
Table 1 Comparison between expanding by 10 data windows with the strongest earthquakes occurrences and windows with IDT values closest to zero. Representative threshold M=2.6.

As we see from Figs. 10–11, at higher representative thresholds (similar to lower threshold M=2.6, in Fig. 9) the strongest earthquakes occur on rising branches of the IDT curve, and that in most cases strong events do no occur in windows where calculated values of IDT come closer to zero.

Further analysis by the same scheme for higher-threshold magnitudes (e.g., M=5.6) was impossible because of the scarce number of large earthquakes in the considered seismic catalog (just 29 earthquakes above M=5.6). At the same time, we point out that even for M=5.6 representative threshold, for the entire period 1975–2017, the results obtained for two or three available windows (29 events at windows expanding by 9 or 10 data) agree with the above results.

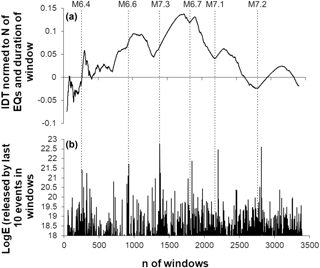
Figure 9 Calculated for the expanding (by consecutive 10 data) windows, integral deviation times (IDTs) (a) and the increments of seismic energies released by 10 last events in consecutive windows (b) obtained from the southern California earthquake catalog (above threshold M=2.6). By the grey lines we show where the IDT curve crosses the abscissa. Dashed lines show the occurrence of largest earthquakes in the catalog.

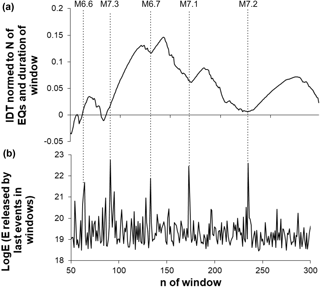
Figure 10 Calculated for the expanding (by consecutive 10 data) windows, integral deviation times (IDTs) (a) and the increments of seismic energies released by 10 last events in consecutive windows (b) obtained from the southern California earthquake catalog (above threshold M=3.6). By the grey lines we show where the IDT curve comes closest to zero value. Dashed lines show the occurrence of largest earthquakes in the catalog.

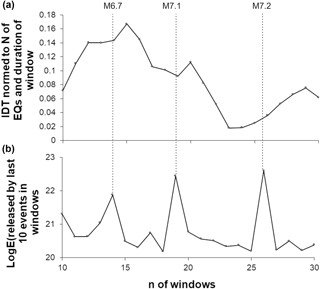
Figure 11 Calculated for the expanding (by consecutive 10 data) windows, integral deviation times (IDTs) (a) and the increments of seismic energies released by 10 last events in consecutive windows (b) obtained from the southern California earthquake catalog (above threshold M=4.6). Dashed lines show the occurrence of the largest earthquakes in the catalog.

Thus, again we conclude that the increase in magnitude threshold (Figs. 10 and 11) practically do not change the results found for the lower representative threshold. This means that by increasing the representative threshold we still deal with the catalog in which relatively small- and medium-size events prevail. Therefore, conclusions drawn from the analysis for original representative threshold (M=2.6) remain correct for the case, when we consider a catalog with relatively stronger events; thus, it seems that there is no principal difference in the character of the contribution of smaller and stronger events to the results of the IDT calculation. Comparison with the results obtained for time-randomized catalogs confirms this conclusion.

Next, in order to avoid doubts related to the fixed starting point in the above analysis, we have carried out the same calculation of IDT values for catalogs which started in 1985, 1990, 1995, 2000, and 2005. As it follows from Tables 1 to 3, analysis carried out on shorter catalogs confirm the result obtained for the entire period of observation (1975–2017) and convinces us that the calculated values of IDT practically never come closer to zero in windows when the strongest earthquakes occur. The only exception is the case of M=6.6 earthquake at representative threshold M=3.6 for the period 1975–2017.

Table 2 Comparison between expanding by 10 data windows with the strongest earthquakes occurrences and windows with IDT values closest to zero. Representative threshold M=3.6.

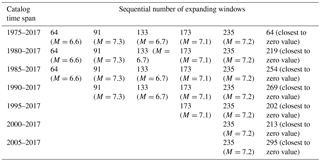
Table 3 Comparison between expanding by 10 data windows with the strongest earthquakes occurrences and windows with IDT values closest to zero. Representative threshold M=4.6.

Thus, we see that shortening the time span of the analyzed part of the catalog does not influence the obtained results.

Because of the above-mentioned unclearness in Figs. 9–11, when we calculated IDTs for the expanding windows and discuss results for the energy release occurred in the last 10 data windows, we performed additional analysis on the sliding windows with fixed number of events. In detail, in the southern California earthquake catalog we have calculated IDT values for non-overlapping windows of 100 consecutive events, shifted by 100 data (Figs. 12, 13). We have used short-sliding windows of 100 data for two reasons: (i) to have good resolution of changes occurring in the time distribution of earthquakes and (ii) because even relatively short, 100 data span windows also provide good enough discrimination in the IDT values, as it is shown in Figs. 5b and 6.

In Fig. 12a, we see that for the entire period of analysis there are dozens of IDT values that are not far from one-tenth of the standard deviation (σ) from zero (given by black circles in the top figure). Most importantly among them, eight IDT values are within 0.01σ of zero. These values of IDT (shown in black in Fig. 12b) can be regarded practically equal to zero. According to the above results on simulated and original data sets, the seismic process in the windows with close-to-zero values of IDT can be regarded as random. If we compare the occurrence of these practically zero IDT values with the amount of seismic energy released in consecutive windows (Fig. 12c), it becomes clear that they occur in periods of essentially decreased (comparing to observed maximums) seismic energy release. A similar conclusion is drawn from the analysis of the catalogs for earthquakes above the M=3.6 threshold (Fig. 13). Because of the restricted number of strong events in the catalog, further increase in the threshold magnitude was impossible for the case of 100 data non-overlapping sliding windows.

Results obtained for non-overlapping sliding windows of fixed length also confirm the results obtained for expanding windows.

The simple statistical approach used here thus shows that the extent of randomness in the earthquake time distributions is changing over time and that it is most random-like at periods of decreased seismic activity. The results of this analysis provide additional indirect arguments in favor of our earlier suggestion that the extent of regularity in the earthquake time distributions should decrease in seismically quiet periods and increase in periods of strong earthquakes preparation (Matcharashvili et al., 2011, 2013).

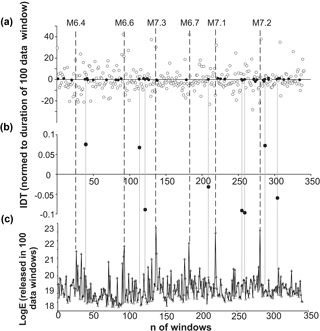
Figure 12 Calculated for the non-overlapping 100 data windows (shifted by 100 data), integral deviation times (IDTs) (circles in panels a and b) and the released seismic energies (c). IDT values in the vicinity of 0.1σ from zero are given by black circles in panel (a). IDT values in the vicinity of 0.01σ from zero are given by black circles in the middle figure. By grey lines we show the location of closest to zero IDT values relative to the released seismic energy. Dashed lines show the occurrence of largest earthquakes in the southern California catalog (above threshold M=2.6).

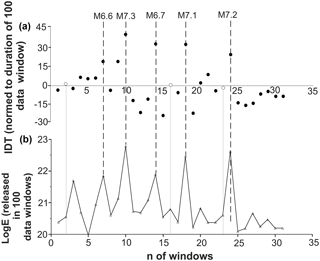
Figure 13 Calculated for the non-overlapping 100 data windows (shifted by 100 data), integral deviation times (IDTs) (circles in panel a) and the released seismic energies (triangle in panel b). IDT values in vicinity of 0.1σ from zero are given by open circles in panel (a). By grey lines we show location of closest to zero IDT values relative to the released seismic energy. Dashed lines show the occurrence of largest earthquakes in the southern California catalog (above threshold M=3.6).

4 Conclusions

We investigated earthquake time distributions in the southern California earthquake catalog by the method of calculation of integral deviation times (IDTs) relative to regular time markers. The main goal of the research was to quantify when the time distribution of earthquakes become closer to the random process. Together with IDT calculation, standard methods of complex data analysis such as power spectrum regression, Lempel and Ziv complexity, and recurrence quantification analysis, as well as multiscale entropy calculations, have been used. Analysis was accomplished for different time intervals and for different magnitude thresholds. Based on a simple statistical analysis result, we infer that the strongest earthquakes in southern California occur only in windows with rising values of IDTs and that the character of the temporal distributions of earthquakes in these windows is less random-like compared to the periods of decreased local seismic activity.