Experimental study of forced convection heat transport in porous media

The present study is aimed at extending this thematic issue through heat transport experiments and their interpretation at laboratory scale. An experimental study to evaluate the dynamics of forced convection heat transfer in a thermally isolated column filled with porous medium has been carried out. The behavior of two porous media with different grain sizes and specific surfaces has been observed. The experimental data have been compared with an analytical solution for one-dimensional heat transport for local nonthermal equilibrium condition. The interpretation of the experimental data shows that the heterogeneity of the porous medium affects heat transport dynamics, causing a channeling effect which has consequences on thermal dispersion phenomena and heat transfer between fluid and solid phases, limiting the capacity to store or dissipate heat in the porous medium.

1 Introduction

The European Climate and Energy Framework for 2050 aims to shift from the massive use of fossil-fuel sources to others characterized by very low emissions. Among the renewable sources, geothermal energy is the only one which is available basically everywhere and at any time.

For this reason, in recent years the use of groundwater as a low-enthalpy geothermal resource for heating and cooling of buildings and for agricultural and industrial processes has been growing.

One of the main limitations for the development of low-enthalpy geothermal systems concerns the high cost of investment. Installation of geothermal energy systems requires high upfront capital investments that often exceed the expectations of depreciation expense, so the investment is therefore inconvenient and the economic benefits can only occur after a long time. It is therefore of extreme importance to further the understanding of the behavior of hydrological systems, particularly concerning heat transport. Studying heat transfer phenomena takes advantage of the fact that the governing partial differential equations used to describe flow and transport processes in porous media are based on the same form of mass and/or energy conservation laws.

Several studies have been already carried out in this context with the aim of enhancing heat transfer phenomena in porous media for engineering processes. Theoretical and numerical research on convection heat transfer in porous media has used two different models for the energy equation: the local thermal equilibrium (LTE) model and the local thermal nonequilibrium model.

Most of the studies have been focused on investigating the validity of the local thermal equilibrium assumption between the solid and fluid phase, the influence of nonlinear flow patterns, and the existing relationship between thermal dispersion and flow velocity.

Koh and Colony (1974) carried out an analytical investigation of the performance of a heat exchanger containing a conductive porous medium using the Darcy flow model, while Koh and Stevens (1975) performed an experimental study of the same problem. They have shown that for a constant heat flux boundary condition the wall temperature is significantly decreased by using a porous material in the channel.

Vafai and Tien (1981) have formulated a general mathematical model that takes into consideration the boundary and inertial (non-Darcian) effects on flow and heat transfer in porous media. In analyzing these effects, they considered three flow resistances: the bulk damping resistance due to the porous structure, the viscous resistance due to the boundary, and the resistance due to the inertial forces.

Later, Vafai and Tien (1982) performed a numerical and experimental investigation of the effects of the presence of a solid boundary and inertial forces on mass transfer in porous media.

Kaviany (1985) studied laminar flow through a porous channel bounded by two parallel plates maintained at a constant and equal temperature by applying a modified Darcy model for transport of momentum.

Vafai and Kim (1989) considered fully developed forced convection in a porous channel bounded by parallel plates by applying a Brinkman–Forchheimer extended Darcy model to obtain a closed-form analytical solution.

Lauriat and Vafai (1991) presented a comprehensive review on flow and heat transfer through porous media for two basic geometries: flow over a flat plate embedded in a porous medium and flow through a channel filled with a porous medium.

Hadim (1994) carried out a numerical study to analyze steady laminar forced convection in a (1) fully porous and (2) partially porous channel filled with a fluid-saturated porous medium and containing discrete heat sources on the bottom wall.

He modeled the flow in the porous medium using the Brinkman–Forchheimer extended Darcy model.

Kamiuto and Saitoh (1994) examined theoretically the effects of several system parameters on the heat transfer characteristics of fully developed forced convection flow in a cylindrical packed bed with constant wall temperatures. They developed a two-dimensional model incorporating the effects of non-Darcian variable porosity and radial thermal dispersion.

Hwang et al. (1995) performed a study of non-Darcian forced convection in an asymmetric heating sintered porous channel to investigate the feasibility of using this channel as a heat sink. The study showed that the particle's Reynolds number significantly affected the solid-to-fluid heat transfer coefficients.

A review of the literature indicates that the local thermal equilibrium assumption between the solid and fluid phase is used in the majority of heat transfer applications involving porous media. Minkowycz et al. (1999) proposed a modified energy equation that can be solved for very early departures from LTE conditions. Their results confirmed that local thermal equilibrium in a fluidized bed depends on the size of the layer, mean pore size, interstitial heat transfer coefficient, and thermophysical properties. They concluded that for a porous medium subject to rapid transient heating, the existence of the local thermal equilibrium depends on the magnitude of a dimensionless quantity (which they called the Sparrow number) containing the contributions of the flow in porous media, interstitial heat transfer, and general thermal conduction.

An in-depth analysis of nonthermal equilibrium is provided by Amiri and Vafai (1994, 1998).

Amiri and Vafai (1994) carried out a steady-state analysis of incompressible flow through a bed of uniform solid sphere particles packed randomly. The investigation was aimed at exploring the influence of a variety of phenomena such as the inertial effects, boundary effects, and the effect of the porosity variation model together with the thermal dispersion effect on the momentum and energy transport in a confined porous bed. They also proved the validity of the LTE assumption and the two-dimensionality effects on transport processes in porous media.

In a subsequent study, Amiri and Vafai (1998) realized a rigorous and flexible model to explore the heat transfer aspects in a packed bed made of randomly oriented spherical particles. Along with the generalized momentum equation they used a two-energy equation model to describe the thermal response of a packed bed. They explored the temporal impact of the non- Darcian terms and the thermal dispersion effects on energy transport. In addition, they investigated on the LTE condition and the one-dimensional approach under transient conditions by formulating dimensionless variables that serve as instruments in depicting the pertinent characteristics of energy transport in a packed bed.

Khalil et al. (2000) performed a numerical investigation of forced convection heat transfer through a packed pipe heated at the surface under constant heat flux, showing the effects of a particle's Reynolds number, pipe-to-particle diameter ratios, and the Prandtl number. They showed that the average Nusselt number increases with both the particle's Reynolds number and the Prandtl number. They concluded that packing pipes with a porous medium can provide heat transfer enhancement for the same pumping power.

Wu and Hwang (1998) investigated, experimentally and theoretically, flow and heat transfer dynamics inside an artificial porous matrix by using a modified version of the local thermal nonequilibrium (LTNE) model, which neglected the effects of thermal dispersion in both fluid and solid. The results showed a highly non-Fourier behavior that combined rapid thermal breakthrough with extremely long-tailing, which was attributed to disequilibrium between the fluid and the porous matrix. However, the adopted model was unable to fully capture the thermal breakthrough observed in some experimental runs. They concluded that heat transfer coefficient increases with the decrease in porosity and the increase in the particle's Reynolds number.

Emmanuel and Berkowitz (2007) were able to successfully fit the thermal breakthrough curves obtained by Wu and Hwang (1998) by applying the continuous time random walk (CTRW), which provided an alternative description of heat transport in porous media. They argued that larger scale spatial heterogeneities in porous media present obstacles to both the equilibrium and the LTNE models and that CTRW would be particularly applicable to the quantification of heat transfer in naturally heterogeneous geological systems, such as soils and geothermal reservoirs.

Geological media are typically characterized by heterogeneities on many scales, resulting in a wide range of fluid velocities, porosities, and effective thermal conductivities.

Despite the uncertainty and contradiction in defining the thermal dispersion, several studies addressed the effects of thermal dispersion in porous media, and different approaches have been developed to describe it (Hsu and Cheng, 1990; Anderson, 2005; Molina-Giraldo et al., 2011).

Thermal dispersion is generally defined as a function of fluid velocity and grain size (Lu et al., 2009; Sauty et al., 1982; Nield and Bejan, 2006).

According to Sauty et al. (1982) and Molina-Giraldo et al. (2011), the thermal dispersion is a linear function of flow velocity and relates to the anisotropy of the velocity field whereas Rau et al. (2012) proposed a dispersion model as a function of the square of the thermal front velocity.

The literature also contains conflicting theories about the magnitude of thermal dispersivity. Smith and Chapman (1983) state that it has the same order of magnitude as solute dispersivities, while Ingebritsen and Sanford (1999) neglect it. According to Vandenbohede et al. (2009) thermal dispersivities are small in comparison to solute dispersivities and are less scale dependent.

Mori et al. (2005) showed experimentally that, for water fluxes ranging between 0.6 × 10⁻⁶ and 0.3 × 10⁻³ (m s⁻¹) thermal dispersion was nearly independent of water flow and its effects were insignificant.

According to Rau et al. (2012), the effect of thermal dispersion on heat transport is significant for high values of thermal Peclet number. Metzger et al. (2004) also introduced a dispersion model based on the thermal Peclet number.

Koch et al. (1989) obtained an analytical expression for the dispersion tensor for a regular arrangement of cylinders or spheres. They found that for high values of Peclet numbers, the ratio of longitudinal total thermal diffusivity to the fluid thermal diffusivity was proportional to the square of the Peclet number while maintaining the transverse dispersion constant. The analytic finding was in good concordance with the experimental measurements of Gunn and Pryce (1969).

Eidsath et al. (1983) quantified the longitudinal thermal dispersion and stressed that the streamwise ratio of longitudinal total thermal diffusivity to the fluid thermal diffusivity was proportional to Pe^1.7.

Ait Saada et al. (2006) investigated the behavior of microscopic inertia and thermal dispersion in a porous medium with a periodic structure by using a local approach at the pore scale to evaluate the velocity and temperature fields as well as their intrinsic velocity and temperature fluctuations in a typical unit cell of the porous medium under study. They concluded that nonlinear effects characterizing microscopic inertia might be the definitive cause of thermal dispersion depending on the nature of the porous medium and in certain situations can exceed 50 % toward the contribution of thermal dispersion. Particularly for a highly conducting fluid moving with high Peclet numbers, microscopic inertial effects were shown to take a great part in the heat transfer duty. They concluded that a considerable interaction between the velocity and thermal fields exists.

This work is aimed at studying the dynamics of forced convection heat transport in porous media, allowing the understanding of how the grain size and the specific surface affect heat transport in terms of macrodispersion phenomena, and heat transfer between solid and fluid phases, and heat storage properties. In particular, the present study involves the experimental investigation of heat transport through a thermally isolated column filled with a porous medium. Several heat tracer tests have been carried out using porous media with different grain sizes. The experimental observed breakthrough curves have been compared with the one-dimensional analytical solution for the forced convection heat transport under local thermal nonequilibrium conditions. The results highlight the effects of grain size and the specific surface on forced convection heat transport dynamics in porous media.

2 Theoretical background

In several studies examining the flow dynamics through porous media it is assumed that flow is described by Darcy's law, which expresses a linear relationship between pressure gradient and flow rate. Darcy's law has been demonstrated to be valid at low flow regimes (Re < 1), whereas for Re ≫ 1 a nonlinear flow behavior is likely to occur. As velocity increases, the inertial effects start dominating the flow field. In order to take these inertial effects into account, Forchheimer (1901) introduced an inertial term representing the kinetic energy of the fluid to the Darcy equation. The Forchheimer equation for one-dimensional flow in terms of hydraulic head h (L) is given as follows:

$$\begin{array}{}\text{(1)}& -{\displaystyle \frac{\mathrm{d}h}{\mathrm{d}x}}={\displaystyle \frac{\mathit{\mu }}{\mathit{\rho }gk}}q+{\displaystyle \frac{{\mathit{\beta }}_F}{g}}{q}^{\mathrm{2}},\end{array}$$

where x (m) is the coordinate parallel to the axis of the one-dimensional porous medium, k (L²) is the permeability, μ (M L⁻¹ T⁻¹) is the viscosity, ρ (M L⁻³) is the density, q (L T⁻¹) is the Darcy velocity, and β_F (L⁻¹) is called the non-Darcy coefficient.

Ergun (1952) derived a model for high-velocity pressure loss in a porous medium from the Forchheimer equation by correlating the permeability and inertial resistance dimensionally to the porosity and the equivalent sphere diameter of rough particles. The permeability and inertial coefficient are interpreted in terms of spatial parameters as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }k={\displaystyle \frac{d_{\mathrm{p}}^{\mathrm{2}}{n}^{\mathrm{3}}}{A{\left(\mathrm{1}-n\right)}^{\mathrm{2}}}},\text{(3)}& {\displaystyle }& {\displaystyle }{\mathit{\beta }}_F={\displaystyle \frac{B\left(\mathrm{1}-n\right)}{d_{\mathrm{p}}{n}^{\mathrm{3}}}},\end{array}$$

where d_p (L) is the average particle diameter, n (–) is the porosity, and the coefficients A = 180 and B = 1.8 are empirical values and were derived by averaging the Navier–Stokes equations for a cubic representative unit volume.

The behavior of convective heat transport in porous media is strongly dependent on the fluid velocity and the kinetics of the heat transfer process between fluid and solid phases.

Given a packed bed, within a thermally isolated column of length L (L) in which a fluid flows with a specific flow rate q (L T⁻¹) and then with an average fluid velocity q∕n, the initial temperature in the column is T₀ (K) and a continuous flow injection transports heat energy along the column. For a small ratio of column diameter D (L) to the length L and large fluid velocity, the radial heat transport dynamics can be neglected in comparison with the axial dynamics. Then the heat transport dynamics in the porous medium column can be represented by a one-dimensional model.

If the solid and fluid phases are in contact for a sufficient period of time, there is the possibility to establish a local thermal equilibrium condition. In such case, only one energy equation is sufficient for the description of the convective heat transport through the porous medium. Assuming that porosity, densities, and heat capacities are constant in time the energy equation for the fluid and solid phases are combined into a single equation as follows:

$$\begin{array}{}\text{(4)}& {\left(\mathit{\rho }c\right)}_{\mathrm{sf}}{\displaystyle \frac{\partial T_{\mathrm{f}}}{\partial t}}={\displaystyle \frac{\partial }{\partial x}}\cdot \left[-vn{\mathit{\rho }}_{\mathrm{f}}{c}_{\mathrm{f}}{T}_{\mathrm{f}}+k_{\mathrm{sf}}{\displaystyle \frac{\partial T_{\mathrm{f}}}{\partial x}}\right],\end{array}$$

with

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle }{\left(\mathit{\rho }c\right)}_{\mathrm{sf}}=\left(\mathrm{1}-n\right){\mathit{\rho }}_{\mathrm{s}}{c}_{\mathrm{s}}+n{\mathit{\rho }}_{\mathrm{f}}{c}_{\mathrm{f}}\text{(6)}& {\displaystyle }& {\displaystyle }{k}_{\mathrm{sf}}=\left(\mathrm{1}-n\right)k_{\mathrm{s}}+n{k}_{\mathrm{f}},\end{array}$$

where T_f (K) is the temperature of the fluid, ρ_f (M L⁻³) is the density of the fluid, ρ_s (M L⁻³) is the density of the solid, c_f (L T² K⁻¹) is the thermal capacitance of the fluid, c_s (L T² K⁻¹) is the thermal capacitance of the solid, k_f (M L T⁻³ K⁻¹) is the thermal conductivity of the fluid, k_s (M L T⁻³ K⁻¹) is the thermal conductivity of the solid, and (ρc)_sf and k_sf represent the equivalent heat capacity and thermal conductivity of the porous domain, respectively, including porosity and thermal properties of solid and fluid.

If the interaction between solid and fluid phase is rapid the solid and fluid phase cannot exchange sufficient amounts of energy to establish local thermal equilibrium. At a given location solid and fluid phases have different temperatures. In the LTNE conditions each phase needs an energy equation for the description of heat transport. Assuming that porosity, densities, and heat capacities are constant in time, the energy equations can be written for the fluid and solid phase:

$$\begin{array}{}\text{(7)}& {\displaystyle }& {\displaystyle }n{\mathit{\rho }}_{\mathrm{f}}{c}_{\mathrm{f}}{\displaystyle \frac{\partial T_{\mathrm{f}}}{\partial t}}={\displaystyle \frac{\partial }{\partial x}}\cdot \left[-vn{\mathit{\rho }}_{\mathrm{f}}{c}_{\mathrm{f}}{T}_{\mathrm{f}}+n{k}_{\mathrm{f}}{\displaystyle \frac{\partial T_{\mathrm{f}}}{\partial x}}\right]+q_{\mathrm{fs}},\text{(8)}& {\displaystyle }& {\displaystyle }\left(\mathrm{1}-n\right){\mathit{\rho }}_{\mathrm{s}}{c}_{\mathrm{s}}{\displaystyle \frac{\partial T_{\mathrm{s}}}{\partial t}}={\displaystyle \frac{\partial }{\partial x}}\cdot \left[\left(\mathrm{1}-n\right)k_{\mathrm{s}}{\displaystyle \frac{\partial T_{\mathrm{s}}}{\partial x}}\right]-q_{\mathrm{fs}},\end{array}$$

The interaction between the two phases is represented by the sink–source terms q_fs given by the following equation:

$$\begin{array}{}\text{(9)}& q_{\mathrm{fs}}=h{s}_{\mathrm{f}}\left(T_{\mathrm{s}}-T_{\mathrm{f}}\right),\end{array}$$

where h (M T⁻³ K⁻¹) is the convective heat transfer coefficient and s_f (L⁻¹) is the specific surface area given by

$$\begin{array}{}\text{(10)}& s_{\mathrm{fs}}={\displaystyle \frac{\mathrm{6}(\mathrm{1}-n)}{d_{\mathrm{p}}}}.\end{array}$$

The convective heat transfer coefficient is related to the Nusselt number Nu that for the porous medium can be expressed as follows:

$$\begin{array}{}\text{(11)}& \mathit{\text{Nu}}={\displaystyle \frac{q_{\mathrm{fs}}{d}_{\mathrm{p}}}{k_{\mathrm{f}}\left(T_{\mathrm{f}}-T_{\mathrm{s}}\right)}}={\displaystyle \frac{h{d}_{\mathrm{p}}}{k_{\mathrm{f}}}}.\end{array}$$

Heat transfer dynamics can also be represented by the volumetric Nusselt number Nu_v:

$$\begin{array}{}\text{(12)}& {\mathit{\text{Nu}}}_{\mathrm{v}}={\displaystyle \frac{h{s}_{\mathrm{f}}{d}_{\mathrm{p}}^{\mathrm{2}}}{k_{\mathrm{f}}}}.\end{array}$$

Wakao et al. (1979) found the following correlation for the volumetric Nusselt number:

$$\begin{array}{}\text{(13)}& {\mathit{\text{Nu}}}_{\mathrm{v}}=\mathrm{2.0}+\mathrm{1.1}{\mathit{\text{Re}}}^{\mathrm{0.6}}{\mathit{\text{Pr}}}^{\frac{\mathrm{1}}{\mathrm{3}}}.\end{array}$$

Fu et al. (1998), Kamiuto and Yeem (2005), and Ando et al. (2013) found, based on experimental data, a correlation between the volumetric Nusselt number and Reynolds number:

$$\begin{array}{}\text{(14)}& {\mathit{\text{Nu}}}_{\mathrm{v}}=C{\mathit{\text{Re}}}^m.\end{array}$$

The hydrodynamic mixing of the interstitial fluid at the pore scale gives rise to significant thermal dispersion phenomena. Generally, the hydrodynamic mixing is due to the presence of obstruction, flow restriction, and turbulent flow. Therefore, the equivalent thermal conductivity in Eq. (4) and thermal conductivity in Eq. (7) is replaced with the effective thermal conductivity k_eff which is the sum of thermal conductivity and thermal dispersion conductivity. The effective thermal conductivity depends on various parameters such as mass flow rate, porosity, shape of pores, temperature gradient, and solid and fluid thermal properties (Kaviany, 1995). The following equation can be used to estimate k_eff.

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{k_{\mathrm{eff}}}{k_{\mathrm{f}}}}={\displaystyle \frac{k}{k_{\mathrm{f}}}}+K\cdot {\mathit{\text{Pe}}}^a\end{array}$$

Pe represents the Peclet number defined as the product between the Reynolds number Re and Prandtl number Pr.

$$\begin{array}{}\text{(16)}& \mathit{\text{Pe}}=\mathit{\text{Re}}\times \mathit{\text{Pr}}={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{f}}v{d}_{\mathrm{p}}}{\mathit{\mu }}}\times {\displaystyle \frac{c_{\mathrm{f}}\mathit{\mu }}{k_{\mathrm{f}}}}={\displaystyle \frac{v{d}_{\mathrm{p}}}{D_{\mathrm{f}}}}\end{array}$$

The energy equation representative of the local thermal nonequilibrium can be written as follows:

$$\begin{array}{}\text{(17)}& {\displaystyle }& {\displaystyle \frac{\partial T_{\mathrm{f}}}{\partial t}}=-v{\displaystyle \frac{\partial T_{\mathrm{f}}}{\partial x}}+D_{\mathrm{eff}}{\displaystyle \frac{{\partial }^{\mathrm{2}}{T}_{\mathrm{f}}}{\partial x}}+\mathit{\alpha }\left(T_{\mathrm{s}}-T_{\mathrm{f}}\right),\text{(18)}& {\displaystyle }& {\displaystyle \frac{\mathrm{1}-n}{n}}{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{s}}{c}_{\mathrm{s}}}{{\mathit{\rho }}_{\mathrm{f}}{c}_{\mathrm{f}}}}{\displaystyle \frac{\partial T_{\mathrm{s}}}{\partial t}}={\displaystyle \frac{\mathrm{1}-n}{n}}{\displaystyle \frac{k_{\mathrm{s}}}{{\mathit{\rho }}_{\mathrm{f}}{c}_{\mathrm{f}}}}{\displaystyle \frac{{\partial }^{\mathrm{2}}{T}_{\mathrm{s}}}{\partial x}}-\mathit{\alpha }\left(T_{\mathrm{s}}-T_{\mathrm{f}}\right),\end{array}$$

with

$$\begin{array}{}\text{(19)}& {\displaystyle }& {\displaystyle }{D}_{\mathrm{eff}}={\displaystyle \frac{k_{\mathrm{eff}}}{{\mathit{\rho }}_{\mathrm{f}}{C}_{\mathrm{f}}}},\text{(20)}& {\displaystyle }& {\displaystyle }\mathit{\alpha }={\displaystyle \frac{h{s}_{\mathrm{f}}}{n{\mathit{\rho }}_{\mathrm{f}}{C}_{\mathrm{f}}}}.\end{array}$$

D_eff (L² T⁻¹) is the thermal dispersion and α (T⁻¹) is the exchange coefficient.

The thermal dispersion happens due to hydrodynamic mixing of fluid at the pore scale caused by the nature of the porous medium. Greenkorn (1983) found nine mechanisms responsible of most of the mixing, among which are the following: (1) mixing caused by the tortuosity of the flow channels due to obstructions – fluid elements starting a given distance from each other and proceeding at the same velocity will not remain the same distance apart; (2) existence of autocorrelation in flow paths – in this case, all pores in a porous medium may not be accessible to a fluid element after it has entered a particular flow path; (3) recirculation due to local regions of reduced pressure due to the conversion of pressure energy into kinetic energy; (4) hydrodynamic dispersion in a capillary caused by the velocity profile produced by the adhering of the fluid to the wall; (5) molecular diffusion into dead-end pores as solute rich front passes the pore. After the front passes, the solute will diffuse back out, thus dispersing.

Using the analogy with the solute transport the Damköhler number Da (Leij et al., 2012) can be introduced in order to evaluate the influence of heat transfer between the fluid and solid phases on the convection phenomena:

$$\begin{array}{}\text{(21)}& \mathit{\text{Da}}={\displaystyle \frac{\mathit{\alpha }L}{v}}.\end{array}$$

When Da reaches the unit the heat transfer timescale is comparable with the convection timescale and the LTNE exists between solid and fluid phases. At very high values of Da the heat transfer timescale is much lower than the convective timescale and the LTE condition exists between solid and fluid phases. Finally, at very low values of Da the heat transfer phenomena between solid and fluid phase can be neglected.

Neglecting the first term on the right side of Eq. (18), the analytical solution of the system equations describing one-dimensional heat transport in a semi-infinite domain for instantaneous temperature injection is given by Goltz and Roberts (1986). According to this analytical solution, the probability of density function PDF_LTNE of the residence time for LTNE condition can be written as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{PDF}}_{\mathrm{LTNE}}\left(x,t\right)=\\ \text{(22)}& {\displaystyle }& {\displaystyle }{e}^{\mathit{\alpha }t}{\mathrm{PDF}}_{\mathrm{0}}\left(x,t\right)+\mathit{\alpha }\underset{\mathrm{0}}{\overset{t}{\int }}H\left(t,\mathit{\tau }\right){\mathrm{PDF}}_{\mathrm{0}}\left(x,t\right)\mathrm{d}\mathit{\tau },\end{array}$$

with

$$\begin{array}{}\text{(23)}& {\displaystyle }& {\displaystyle }{\mathrm{PDF}}_{\mathrm{0}}\left(x,t\right)={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathit{\pi }{D}_{\mathrm{eff}}t}}}\exp \left({\displaystyle \frac{x-vt}{\mathrm{4}{D}_{\mathrm{eff}}t}}\right),\text{(24)}& {\displaystyle }& {\displaystyle }H\left(t,\mathit{\tau }\right)=e^{-\frac{\mathit{\alpha }}{\mathit{\beta }}\left(t-\mathit{\tau }\right)-\mathit{\alpha }\mathit{\tau }}{\displaystyle \frac{\mathit{\tau }{I}_{\mathrm{1}}\left(\frac{\mathrm{2}\mathit{\alpha }}{\mathit{\beta }}\sqrt{\mathit{\beta }\left(t-\mathit{\tau }\right)\mathit{\tau }}\right)}{\sqrt{\mathit{\beta }\left(t-\mathit{\tau }\right)\mathit{\tau }}}},\text{(25)}& {\displaystyle }& {\displaystyle }\mathit{\beta }={\displaystyle \frac{\mathrm{1}-n}{n}}{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{s}}{c}_{\mathrm{s}}}{{\mathit{\rho }}_{\mathrm{f}}{c}_{\mathrm{f}}}},\end{array}$$

where PDF₀(x,t) represents the probability density function of the residence time without heat transfer between the solid and fluid phase. The parameter β (–) represents the ratio of the volume-specific heat capacity of the solid phase to the fluid, and I₁ is the modified Bessel function of order 1.

The coefficient α can be viewed as the reciprocal of the exchange time required to transfer energy from fluid to solid phase and vice versa. The effect of local thermal nonequilibrium is stronger when the exchange time is the same order of magnitude of the transport time. The local thermal nonequilibrium is characterized by a thermal distribution profile with a tailing effect.

The observed temperature function T_obs(t) at a generic distance x from the injection temperature function T_inj(t) can be obtained using the convolution theorem:

$$\begin{array}{}\text{(26)}& T_{\mathrm{obs}}(x,t)=T_{\mathrm{inj}}(\mathrm{0},t)\cdot {\mathrm{PDF}}_{\mathrm{LTNE}}\left(x,t\right).\end{array}$$

3 Experimental setup

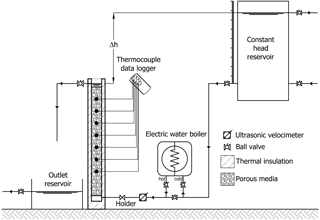
The test on convective heat transport in the porous medium has been conducted on a laboratory physical model. Figure 1 shows a sketch of the experimental setup. A plastic circular pipe characterized by a diameter of D = 0.11 m and height of H = 1.66 m has been thermally insulated using a roll of elastomeric foam with a thickness of s = 0.04 m and a thermal conductivity of λ = 0.037 W m⁻¹ K⁻¹. The pipe can be filled with different porous materials with different grain sizes and hydrothermal properties. Seven thermocouples have been equally placed along the axis of the pipe with a reciprocal distance of 0.185 m. The first thermocouple is located at a distance of 0.435 m from the inlet of the water. The TC08 Thermocouple Data Logger (Pico Technology) with sampling rate equal to 1 s has been connected with the thermocouples. An adaptable constant head reservoir and an outlet reservoir permit a constant head to be maintained during the test, and water within the pipe flows from the bottom to the top. An ultrasonic velocimeter (DOP3000 by Signal Processing) is used to measure the instantaneous flow rate. An electric water boiler characterized by a volume equal to 0.01 m³ has been used to heat the water flowing through the pipe.

A medium gravel (M₁) (Soil Survey Staff, 1975) and a very coarse gravel (M₂) (Soil Survey Staff, 1975) have been used. Figure 2 shows the tested materials whereas in Table 1 the hydraulic and the thermal parameters of each material are reported. The grain size and the specific surface of each porous material is directly estimated on a sample of 100 grains, whereas the porosity is estimated by the ratio of the volume of void space to the total volume of the filled plastic circular pipe. The volume of the void space is obtained by measuring the amount of water which enters the pipe until full saturation. The thermal characteristics reported in the Table 1 are literature values (Engineering ToolBox, 2009). The temperature tracer tests involve the observation of the thermal breakthrough curves (BTCs) monitored by the seven thermocouples. Initially cold water flows through the pipe filled with the porous medium in order to have a constant temperature T₀ along the pipe. Subsequently hot water flows through the pipe, maintaining a constant head condition during the test.

Figure 1 Setup of experimental apparatus.

4 Discussion

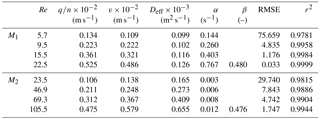
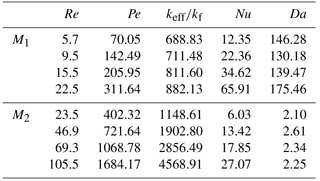
For each tested porous medium four thermal tracer tests have been carried out varying Re in the range 5.7–22.5 for M₁ and 23.5–105.5 for M₂. The thermal BTCs observed at different distances have been fitted together using Eq. (19). The root mean square error (RMSE) and the determination coefficient (r²) have been used as criteria to evaluate the goodness of fit. The parameters v, D_eff, and α have been individually fitted for each thermal tracer test whereas β has been imposed constant for all tracer tests of each tested porous medium. Table 2 shows the estimated values of the heat transport parameters, the RMSE, and r², whereas Figs. 3 and 4 show the fitting results of the observed temperature distribution along the porous column for M₁ and M₂ respectively. Table 3 shows the dimensionless numbers Pe, k_eff∕k_f, Nu, and Da evaluated for the different values of Re.

Figure 2 Samples of the materials used for the experiments with different average grain sizes d_p: (a) d_p = 9.2 mm, (b) d_p = 41.6 mm.

Table 1 Properties of the porous materials.

Table 2 Estimated values of parameters for LTNE model for different Re values.

As shown in Table 2, the fluid velocity q∕n is systematically higher than the estimated thermal convective velocity v for the medium gravel M₁; on the contrary, for the very coarse gravel, M₂q∕n is systematically lower than v.

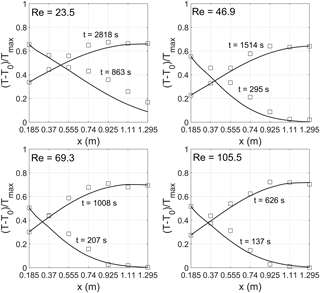
Figure 3 Temperature distribution for increasing Re values along the porous column filled with material M₁. The two curves represent the inlet and the downstream temperature. Squares represent the experimental values, the continuous lines represent the simulated values.

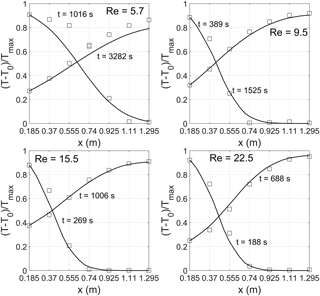
Figure 4 Temperature distribution for increasing Re values along the porous column filled with material M₂. The two curves represent the inlet and the downstream temperature. Squares represent the experimental values, continuous lines represent the simulated values.

This phenomenon for the coarser material might be attributable to the fact that the heat propagates through both the solid and fluid phase (Anderson, 2005; Rau et al., 2012) and to the existence of channeling phenomena that might also have an influence in increasing the convective heat.

Even for finer grained materials (2 mm), Rau et al. (2012) also found values of thermal velocity systematically lower than solute velocity, coherent with Bodvarssoon (1972), Oldenburg and Pruess (1998), and Geiger et al. (2006).

Another discrepancy has been observed when comparing the values of the porosity presented in Table 1 and the value of porosity obtained from Eq. (18) equal to 0.467 and 0.469 respectively for M₁ and M₂. For M₁ the value of porosity presented in Table 1 reaches the value derived from β, whereas for M₂ the value presented in Table 1 is higher than the value derived from β.

These results highlight that for M₂ there is the existence of stagnant zones which reduce the amount of porosity that contributes to fluid flow. In other words, in M₁ the total porosity reaches to the effective porosity, whereas in M₂ the effective porosity is less than total porosity.

In other words, because the coarser material M₂ is less well sorted than the less coarse material M₁, not all pores of the former are actually interconnected. In geologic materials, based on the connectivity of pores, consequently, the void space can be divided into interconnected pore, isolated pore, and blind pore (Hu et al., 2017). Only the pores that are well interconnected provide continuous channels for heat and mass transfer and fluid flow, while the pores that are not part of a continuous channel network do not contribute. These pores are known as noneffective pores, namely, they provide no space for fluid flow and heat transfer in reservoirs.

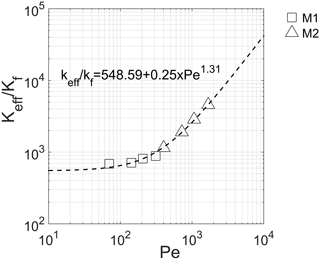
Figure 5 shows the relationships between Pe and the ratio of the effective thermal conductivity to the fluid thermal conductivity k_eff∕k_f. The experimental results show a nonlinear behavior well represented by Eq. (15). A change of slope is evident when changing from M₁ to M₂. The latter material shows a more pronounced thermal dispersion caused by the hydrodynamic mixing of fluid at the pore scale. Some mixing is caused by the tortuosity of the flow paths due to the presence of obstructions: the fluid elements starting a given distance from each other and proceeding at the same velocity will not remain at the same distance apart. The high level of flow path heterogeneity gives rise to a higher velocity variation at pore scale as well as the presence of the preferential flow paths that enhance the effect of macrodispersion. Mixing can also be caused by recirculation caused by local regions of reduced pressure arising from flow restrictions.

Table 3 Dimensionless numbers Pe, k_eff∕k_f, Nu, and Da calculated for different Re values.

Further mixing can arise from the fact that all pores in a porous medium may not be accessible to a fluid element after it has entered a particular flow path.

These results are coherent with those obtained by Rau et al. (2012) who found that the thermal dispersion was transitioning between not depending on the flow velocity and a nonlinear increase with velocity. They affirmed that the location of the transition zone is a function of the thermal properties of the solid and the sedimentological architecture.

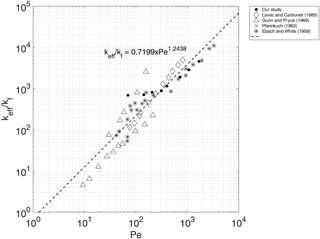
In Fig. 6 the obtained experimental relationship between Pe and k_eff∕k_f has been compared with the results obtained by several authors (Levec and Carbonell, 1985a, b; Gunn and Pryce, 1969; Pfannkuch, 1963; Ebach and White, 1958). For the range of Pe investigated the experimental results presents the same order of magnitude of k_eff∕k_f. For low Peclet numbers the experimental value of k_eff∕k_f is systematically greater than the value of the trend line. This phenomenon can be attributable to the density gradients which altered the flow pattern. Given that the water flows from the bottom to the top and the hot water is fed from the bottom, the buoyancy effect adds to the diffusion effect. This effect seems relevant from low Pe values.

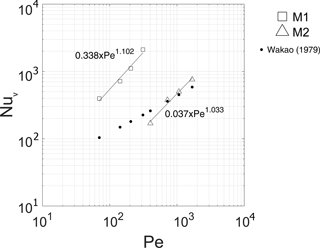
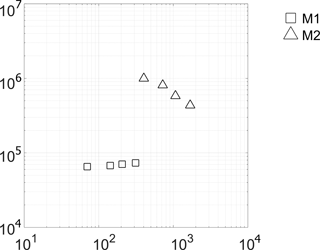
Figure 7 highlights the experimental correlation between Nu_v and Re. Equation (13) fails to represent the experimental results, especially for M₁ where they are underestimated by an order of magnitude. For M₂ the theoretical model reaches the experimental results with a percentage error of 5–35 %.

Figure 5 Relationship between Pe and k_eff∕k_f.

Figure 6 Comparison between the obtained experimental results with other experiments.

According to Ando et al. (2013) the volumetric Nusselt number is well represented by Eq. (14). The exponent m approaches the unit whereas the constant C assumes equal values for M₁ and for M₂. According to Ando et al. (2013) the coefficient C decreases as the pore diameter (correlated with the particle diameter) increases.

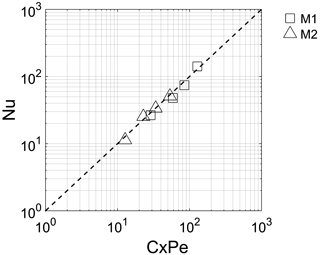
Figure 8 shows the relationship between Pe and Nu. The experimental results highlight that the Nusselt number can be represented by an equation like Nu = C × Pe, where C (–) is a coefficient that assumes a value equal to 0.41 for M₁ and 0.03 for M₂.

Figure 7 Relationship between Pe and Nu_v.

The physical meaning of the ratio of the surface of the grains in contact with the active flow path that transports heat to the total surface of the grain can be attributed to this coefficient. M₂, in comparison to M₁, is characterized by the presence of preferential flow paths and then an equal number of Pe corresponding to a lower Nu because the surface of the grain available to exchange heat between the fluid and solid phase is lower.

As shown in Table 3 the Damköhler number Da calculated for M₁ is greater than the unit. Heat exchange is so rapid that it gives rise to an instantaneous equilibrium between the solid and fluid phase. The heat has enough time to diffuse in the solid phase. On the contrary Da calculated for M₂ is close to the unit, and there is the presence of the local thermal nonequilibrium condition.

Figure 8 Relationship between C × Pe and Nu.

A comparison of the heat J (M L² T⁻²) stored in the porous column per unit temperature difference $\mathrm{\Delta }T=T_{\mathrm{inj}}-T_{\mathrm{0}}$ (K) when varying the specific discharge q for each tested porous medium can be evaluated considering a continuous temperature injection function as follows:

$$\begin{array}{}\text{(27)}& {\displaystyle \frac{J}{\mathrm{\Delta }T}}={\mathit{\rho }}_{\mathrm{f}}{c}_{\mathrm{f}}Q\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\left(\mathrm{1}-\underset{\mathrm{0}}{\overset{t}{\int }}\mathrm{PDF}\left(L,\mathit{\tau }\right)\mathrm{d}\mathit{\tau }\right)\mathrm{d}t.\end{array}$$

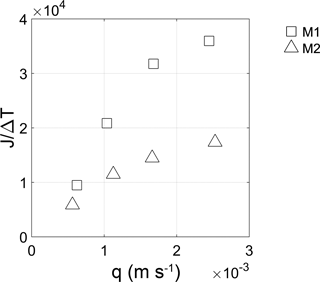
The combined effects of the flow rate and the particle diameter on heat transfer are illustrated in Fig. 9, which shows the variation of the heat stored in the column per unit temperature difference when varying the specific flow rate for M₁ and M₂. As the flow rate increases, the stored heat increases, and the porous medium with a smaller particle diameter generates a higher increase in heat transfer enhancement than that with a larger particle diameter. This is coherent with the results obtained by Dehghan and Aliparast (2011). M₁ permits the storage of more heat than M₂. The former is characterized by a more homogeneous flow path distribution that allows a greater interaction between fluid and solid phase. On the contrary M₂ has a more heterogeneous flow path distribution that increases thermal macrodispersion phenomena at the pore scale and at the same time reduces the interaction between the fluid and solid phase.

Figure 9 Heat exchanged $J/(T_{\mathrm{inj}}-T_{\mathrm{0}})$ varying the specific rate q (m s⁻¹).

Figure 10 Nusselt number–head loss ratio varying the Peclet number.

In order to put into evidence the performance of the heat transfer enhancement of the porous materials it can be useful to compare the Nusselt number and the hydraulic head loss dh∕dx evaluated by Eq. (1). Figure 10 shows the ratio of the Nusselt number to head loss as function of the Peclet number. Despite M₁ presenting a higher heat transfer enhancement with respect to M₂, the head losses are higher and then the ratio of Nu to dh∕dx is lower. Furthermore, as Pe increases, the heat transfer enhancement increases more rapidly than the head loss for the fine material M₁, whereas for the coarser material M₂ the opposite happens: increasing the Peclet number causes a weak increase in the Nusselt number due to the presence of channeling phenomena that reduce the heat exchange area between fluid and solid phases.

5 Conclusion

In this study a laboratory physical model has been set up to analyze the behavior of forced convective heat transport in two porous media characterized by different grain sizes and specific surfaces. For each material four tracer tests have been carried out and they have been compared with the one-dimensional analytical solution of LTNE model. The flow path heterogeneity that characterizes the coarser material gives rise to a higher velocity variation at pore scale with a channeling effect which causes (1) the increase in the macrodispersion phenomena in the forced convection heat transport, (2) the decrease in the surface of the grain available to exchange heat between the fluid and solid phase, (3) the presence of the local thermal nonequilibrium condition (4) the decrease in the amount of heat that can be stored in the porous medium, and (5) a weak growth of heat transfer enhancement respect to the head loss as convective phenomena increases.

The finer material M₁ has a more homogeneous flow path distribution that allows a greater interaction between fluid and solid phase and therefore allows the storage of more heat than the coarser one.

This can also be seen when analyzing the ratio of the Nusselt number to the head loss as function of Peclet number for both materials. Even though the coarser material M₂ is more permeable than M₁ as the advective phenomena increase, the head loss increases more rapidly than the heat transfer enhancement due to the channeling effect that increases the macrodispersion phenomena and reduces the heat transfer between fluid and solid phase.

The main contribution of this study is to investigate the optimal thermal energy storage of porous materials by analyzing how the grain size and the specific surface affect heat storage properties as well as heat transport in terms of macrodispersion phenomena, heat transfer between solid and fluid phases. This is relevant in order to optimize the efficiency of geothermal installations in aquifers.

The experimental results emphasize the differences between porous and fractured media. As observed by Cherubini at al. (2017) a fractured medium with a high density of fractures and then with a higher specific surface is not efficient to store thermal energy because the fractures are surrounded by a matrix with a more limited capacity to store heat. An opposite behavior has been observed in porous media in which a higher specific surface corresponds to a higher capacity to store heat. For porous media, as the specific surface decreases the macrodispersion phenomena increase due essentially to the channeling effect, and then the surface of the grain available to exchange heat between the fluid and solid phase decreases. However, for the fractured media this statement is not true because the macrodispersion phenomena are, in contrast, more related to the roughness and aperture variation of each single fracture as well as to the connectivity of the fracture network.

The study has increased the understanding of heat transfer processes in the subsurface, encouraging the investigation into how further parameters such as the shape and the roughness of the grain of porous media affect the amount of energy that can be stored. This is important to maximize the efficiency and minimize the environmental impact of the geothermal installations in groundwater.