Multifractal analysis of wind turbine power and rainfall from an operational wind farm – Part 1: Wind turbine power and the associated biases

The inherent variability in atmospheric fields, which extends over a wide range of temporal and spatial scales, is also transferred to energy fields extracted from them. In the specific case of wind power generation, this can be seen in the theoretical power available for extraction and the empirical power produced by turbines. To model and analyse them, it is important to quantify their variability, intermittency, and correlations with other interacting fields across scales. To understand the uncertainties involved in power production, power outputs from four 2 MW turbines are analysed (from an operational wind farm at Pay d'Othe, 110 km south-east of Paris, France) using the scale-invariant framework of universal multifractals (UM). Their scaling properties were compared with power available at the same location from simultaneously measured wind velocity.

While statistically analysing the turbine output, the rated power acts like an upper threshold that results in biased estimators. This is identified and quantified here using the theoretical framework of UM and validated using numerical simulations. Understanding the effect of instrumental thresholds in statistical analysis is important in retrieving actual fields and modelling them, more so in wind power production, where the uncertainties due to turbulence are already a leading challenge. This is expanded in Part 2, where the influence of rainfall on power production is studied across scales using UM and joint multifractals.

1 Introduction

In the increasing global transition towards renewable and carbon-neutral energy, wind power is extremely attractive, as it has some of the lowest carbon emissions in life cycle assessment (Li et al., 2020; Guezuraga et al., 2012; Wiser et al., 2011). The levelized cost of energy (LCOE, including building and operation) has also decreased drastically in recent decades for both offshore and onshore wind power (80 % since early 1980 and a further 30 % in the past 5 years), giving it better economic value (Beiter et al., 2021). However, wind is a fluctuating field and mainly owes its generation to uneven heating of Earth's surface by solar radiation and the pressure gradients generated from it. Further, atmospheric turbulence makes the characterization of the field a difficult task (with the governing Navier–Stokes equations still remaining unsolvable). The small-scale fluctuations and intermittency in wind are transferred to the power produced; this is further complicated by the fact that wind turbine hubs are located in the atmospheric boundary layer. In addition, an improved understanding of turbulence is identified as one of the leading challenges in the field of wind power by experts (van Kuik et al., 2016). When it comes to the working of modern turbines, one way to account for wind variations is through variable speed turbines and adaptive torque control enabling maximum power capture. However, the commonly used parameter for control, “turbulence intensity” (standard deviation of wind speed divided by mean wind speed over 10 min), cannot fully capture the behaviour (see the non-Gaussian behaviour of wind velocity in Fig. 1) and is too coarse to represent the variability (active torque controls should be responsive down to a few seconds). Further, this does not consider any effect of rain that could get transferred to loads on turbines (Johnson, 2004).

To understand the complex effect of turbulence on power production, along with access to high-resolution data, an appropriate theoretical framework is required to characterize intermittency at all scales of measurement. The scale-invariant multifractal framework of universal multifractals (UM), which is widely used to study variability in geophysical fields, can be used to characterize this complexity (Schertzer and Lovejoy, 1987, 1997). Using the framework of UM, Fitton et al. (2011, 2014) studied scaling behaviour and multifractal properties of wind velocity and torque fluctuations at wind farm test sites (in Germany and Corsica) and made a case for multifractal modelling of atmospheric turbulence. Multi-fractality of wind speed and aggregate wind farm power was illustrated in Calif and Schmitt (2014), where the coupling between both fields was examined.

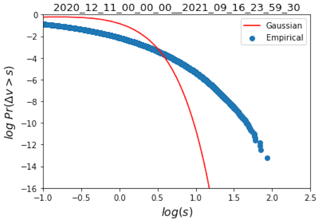
Figure 1 Log–log plot of the exceedance probability, Pr(Δv>s), of only positive horizontal velocity increments, $\mathrm{\Delta }v\left(\mathit{\tau }\right)=v(t+\mathit{\tau })-v\left(t\right)$, from December 2020 to July 2021, at 1 Hz from location 1 of the RW-Turb meteorological mast along with a Gaussian distribution to illustrate the latter's inadequacy. s is a threshold of intensity, and τ here is 15 s.

In light of the scientific perspectives mentioned so far, here we try to characterize the small-scale fluctuations in wind power production using data from an operational wind farm at Pays d'Othe, 110 km south-east of Paris, France. However, while analysing the variability of the field using statistical methods, the presence of instrumental limits in the data can introduce biases. For example, the effect of an instrumental lower threshold is discussed in Jose et al. (2021) in the framework of UM analysis using an atmospheric extinction coefficient (σ_e) as the field. Similarly, there is also bias from the presence of zeroes in the data (Gires et al., 2014). Both of these biases are present in statistical analyses of empirical power from wind turbines since turbines are designed to work at a rated power (here, 2 MW) and can provide zero or negative power (more consumption than production). The major aim of this paper is to highlight these biases encountered during multifractal analysis and their influence on the direct statistical analysis of turbine power. For the theoretical aspect, only the effect of the upper threshold, which has not yet been addressed in the literature, is considered here to avoid complexity. More analysis is intended for a follow-up paper, where the influence of rain on wind power production is examined along with the coupling of power as a field with other atmospheric parameters. The details of the data collection and quality are presented in the following section on data and methods; the second part of this section briefly recapitulates the framework of UM. The biases encountered in the analysis of turbine power are presented in the section that follows, along with numerical simulations where it is identified and reproduced in the framework of UM. Acknowledging these biases, some efforts were made to characterize the effect of rainfall and wind velocity on turbine power. The final section concludes the study and summarizes the results.

2 Data and methods

2.1 Data and instrumentation

The Rainfall Wind Turbine or Turbulence project (RW-Turb; https://hmco.enpc.fr/portfolio-archive/rw-turb/, last access: 26 November 2024), supported by the Agence Nationale de la Recherche (ANR, French National Research Agency in English), is designed to understand the long- and short-term effects of rainfall on wind power production, with simultaneous high-resolution measurements on an operational wind farm. Interested readers are directed to Gires et al. (2022) for an overview of the campaign. To briefly summarize this, the RW-Turb measurement campaign (at Pay d'Othe, 110 km south-east of Paris, France) consists of a meteorological mast (Fig. 2b on the right side) on a wind farm (jointly operated by Boralex, https://www.boralex.com/our-projects-and-sites/, last access: 26 November 2024), and JP Énergie Environnement, https://pays-othe-89.parc-eolien-jpee.fr/, last access: 26 November 2024). Figure 2a shows the location of the project; the nine wind turbines of the Pays d'Othe wind farm (aligned south-east and within a 4 km radius) are marked as black vertical crosses and the meteorological mast as a star (in the middle). Data from four Vestas V-90 (marked 1, 2, 8, and 9 in Fig. 2a) instruments are available: two are closer to the meteorological mast and two are farther from it (≈3.5 km from the mast). The five turbines of the Molinons wind farm in the north are also visible within a 5 km radius (grey vertical crosses). It should also be noted that a small groove is located just south of the mast at roughly 160 m; a larger one is to the east at roughly 100 m. Nearby the mast (i.e. within the 1 km radius), there is a small slope in the north–south direction. The meteorological mast consists of two sets of optical disdrometers (OTT Parsivel², 30 s, not used in current study), 3D sonic anemometers (ThiesCLIMA, 100 Hz), and a mini meteorological station (1 Hz) at heights of roughly 45 and 80 m (managed by the Hydrology Meteorology and Complexity laboratory of the École des Ponts ParisTech – HM&Co, ENPC).

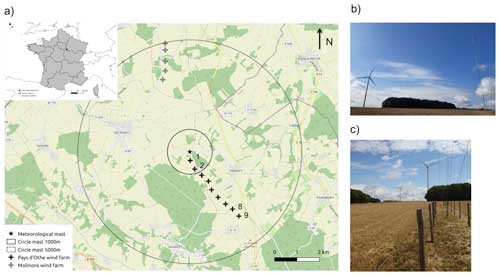
Figure 2 (a) Map of the Pays d'Othe wind farm (inset: location in France): the meteorological mast is at the centre, and the available turbines are numbered – 1, 2, 8, and 9. (b) Turbine 1 and the mast. (c) Turbines 1 and 2 as seen from the bottom of the mast. The figures are adapted from Gires et al. (2022).

Technical and working information on the turbine can be found in Vestas Wind Systems A/S (2023). The turbines have a rated power of 2.0 MW, which is pitch-regulated with variable speed. The hub height of the turbines is 80 m, which is closer to the vertical height of the upper set of devices on the mast (≈78 m). The turbines have a cut-in wind speed of 4 m s⁻¹ and a rated wind speed of 12 m s⁻¹. This can be seen in the power curves in Fig. 3 (last row), where the turbine register power at the cut-in speed maintains the rated power of 2000 kW after the rated wind speed. The cut-out speed of the turbine is 25 m s⁻¹ (the extreme x-axis point of the power curves): this is the speed at which a turbine stops registering power. Generally, the turbines register positive values of wind power. However, when the power retrieved from wind is less than what is required to work a turbine, it registers negative power. This can be seen in the power curves as clusters around 0. Along with the wind power, the turbine also provides information on the local velocity (at a sampling measurement rate of 15 s), which is used for internal regulation; this is used to plot the power curves in Fig. 3. The wind power data used for the studies come from the four turbines of Boralex – 1 and 2 are located closest to the mast (as can be seen in Fig. 2b), and 8 and 9 are located at the farthest end (at a sampling frequency of 15 s).

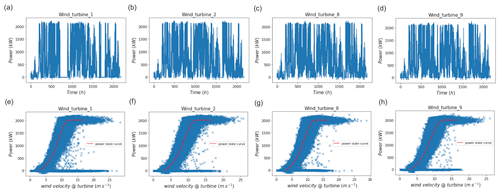
Figure 3 Time series of the empirical turbine power (first row) and the power vs. velocity plot with the theoretical state curve of the turbine (second row) for the wind turbines (1, 2, 8, and 9) at Pays d'Othe.

The temporal evolution and power curves (power vs. velocity, with the expected curve provided by the manufacturer in red) for the turbines are shown in Fig. 3 for 3 months (from 1 January to 1 April 2021). There are instances where the turbine failed to produce any power and had to consume energy for its basic operation. This results in negative data values, and for realistic analysis they were considered to be zero. This is why there is clustering of points at zero in the power curve (Fig. 3e–h).

In addition to the empirical power provided by turbines, the theoretical power available for extraction can be obtained by

$$\begin{array}{}\text{(1)}& P_{\mathrm{a}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }A{v}^{\mathrm{3}}{C}_{\mathrm{p}},\end{array}$$

where ρ is the air density at the wind turbine height (h_hub), A the swept area of the turbine rotor, v the wind velocity (m s⁻¹) approximated at the turbine height, and C_p the power coefficient or Betz coefficient (for the Vestas V-90 instruments examined here, h_hub=80 m, A=6362 m², the rated power is 2 MW, and C_p is 0.593). Here, P_a is estimated at the same sampling rate as that of P_t (15 s) despite the 3D sonic anemometer and mini meteorological station registering data at finer sampling rates.

The value of air density is often approximated as 1.255 kg m⁻³ (standard value at sea level 15 °C). However, it is known to show fluctuations and is reported to have an effect on power generation at varying levels (Jung and Schindler, 2019; Ulazia et al., 2018). For the purpose of this analysis, air density was considered a varying quantity and estimated using the current official formula of the International Committee for Weights and Measures (CIPM), referred to as the CIPM-2007 equation, which accounts for humidity (Picard et al., 2008):

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\mathit{\rho }(T,P,H_r)& ={\displaystyle \frac{P{M}_{\mathrm{a}}}{Z(T,P,H_r)RT\left(K\right)}}\\ & \times \left\{\mathrm{1}-x_{\mathrm{v}}(T,P,H_r)\left[\mathrm{1}-{\displaystyle \frac{M_{\mathrm{v}}}{M_{\mathrm{a}}}}\right]\right\},\end{array}\end{array}$$

where T (°C), P (Pa), and H_r ($\mathrm{0}\le H_r\le \mathrm{1}$) are the temperature, pressure, and humidity from the meteorological station at h_hub. The other derived parameters are the following:

• T(K) the air temperature (K; from T);

• Z the compressibility factor (a function of T and P);

• R the molar gas constant (J mol⁻¹ K⁻¹);

• x_v the mole fraction of water vapour;

• M_a the molar mass of dry air (g mol⁻¹); and

• M_v the molar mass of water (g mol⁻¹).

2.2 Scaling analysis and UM framework

Spectral analysis is widely used for characterizing scaling properties; here, the second-order statistics of rain in the frequency domain were examined for power law scaling as follows (Mandelbrot, 1982; Schertzer and Lovejoy, 1985):

$$\begin{array}{}\text{(3)}& E\left(k\right)\approx k^{-\mathit{\beta }},\end{array}$$

where k corresponds to the wave number and β is the spectral exponent.

However, to fully characterize the complexity of the process across its intensities and spatio-temporal variation, information on higher- and lower-order statistics is required. For this, we use UM, which rely on the assumption of the field being generated by an underlying cascade process with conserved statistical properties at each scale while inheriting the scale-invariant properties of Navier–Stokes equations (Schertzer and Lovejoy, 1987, 1989; Schertzer and Tchiguirinskaia, 2020). In this framework, the probability of a field exceeding a particular threshold across all the scales is captured using the scale-invariant notion of singularity (γ), and for a multifractal field this probability scales according to the resolution (λ: the ratio of L, the outer scale, to l, the observational scale), with a corresponding fractal co-dimension as the scaling exponent c(γ) (Schertzer and Lovejoy, 1987, 1988):

$$\begin{array}{}\text{(4)}& p({\mathit{ϵ}}_{\mathit{\lambda }}\ge {\mathit{\lambda }}^{\mathit{\gamma }})\approx {\mathit{\lambda }}^{-c\left(\mathit{\gamma }\right)}.\end{array}$$

This relation implies that the statistical moments q of the field also scale with resolution and the moment scaling function K(q) as (Schertzer and Lovejoy, 1987, 1988)

$$\begin{array}{}\text{(5)}& \langle {{\mathit{ϵ}}_{\mathit{\lambda }}}^q\rangle \approx {\mathit{\lambda }}^{K\left(q\right)}.\end{array}$$

Both functions are related by Legendre transform (Parisi and Frisch, 1985). For a conservative field in the UM framework, K_c(q) can be fully determined with only two parameters, the multifractality index α and the mean intermittency co-dimension C₁.

$$\begin{array}{}\text{(6)}& K_{\mathrm{c}}\left(q\right)=\left\{\begin{array}{ll}{\displaystyle \frac{C_{\mathrm{1}}}{\mathit{\alpha }-\mathrm{1}}}(q^{\mathit{\alpha }}-q)& \mathit{\alpha }\ne \mathrm{1}\\ C_{\mathrm{1}}q\ln q& \mathit{\alpha }=\mathrm{1}\end{array}\right.\end{array}$$

C₁ measures the clustering of average intensity across scales ($C_{\mathrm{1}}\in [\mathrm{0},\mathrm{1}]$ for one-dimensional fields); when C₁=0, the field is homogeneous with little variability. α measures how this clustering changes with respect to intensity levels ($\mathit{\alpha }\in [\mathrm{0},\mathrm{2}]$): the higher the value of α, the higher the variability, with α=0 being a mono-fractal field where intermittency of the extreme is the same as that of the mean. If the UM parameters are known, the co-dimension function of the conservative multifractal field c_c(γ) can also be obtained using Lengendre transform (Schertzer and Lovejoy, 1987, 1988; Parisi and Frisch, 1985):

$$\begin{array}{}\text{(7)}& c_{\mathrm{c}}\left(\mathit{\gamma }\right)=\left\{\begin{array}{ll}{C}_{\mathrm{1}}{\left({\displaystyle \frac{\mathit{\gamma }}{C_{\mathrm{1}}{\mathit{\alpha }}^{\prime }}}+{\displaystyle \frac{\mathrm{1}}{\mathit{\alpha }}}\right)}^{{\mathit{\alpha }}^{\prime }}& \mathit{\alpha }\ne \mathrm{1},\\ C_{\mathrm{1}}\exp \left({\displaystyle \frac{\mathit{\gamma }}{C_{\mathrm{1}}}}-\mathrm{1}\right)& \mathit{\alpha }=\mathrm{1},\end{array}\right.\end{array}$$

where $\frac{\mathrm{1}}{\mathit{\alpha }}+\frac{\mathrm{1}}{{\mathit{\alpha }}^{\prime }}=\mathrm{1}$.

For a non-conservative field ϕ_λ, i.e. a field whose average (〈ϕ_λ〉) changes with scales, a non-conservative parameter H (not to be confused with the Hurst exponent: though for values >0 both quantify long-range correlations, the latter does not have a simple general expression for the multifractal process; see the Appendix A for more details) is used in the expression of scaling (Schertzer and Lovejoy, 1987, 1988; Lovejoy and Schertzer, 2013):

$$\begin{array}{}\text{(8)}& {\mathit{\varphi }}_{\mathit{\lambda }}{=}^{\mathrm{d}}{\mathit{ϵ}}_{\mathit{\lambda }}{\mathit{\lambda }}^{-H},\end{array}$$

where =^d denotes equality in the distribution ($X{=}^{\mathrm{d}}Y\iff \forall x:\text{Pr}(X>x)=\text{Pr}(Y>x)$) and ϵ is a conservative field characterized by C₁ and α for a conservative field H=0. For a non-conservative field with positive H, fractional differentiation is required to retrieve a coarser field. Similarly, from a non-conservative field with a negative value of H, the conservative field is retrieved through fractional integration. H is related to the spectral slope β (Eq. 3) via the relationship (Tessier et al., 1993)

$$\begin{array}{}\text{(9)}& \mathit{\beta }=\mathrm{1}+\mathrm{2}H-K_{\mathrm{c}}\left(\mathrm{2}\right).\end{array}$$

The scaling behaviour of conservative multifractal fields can be examined using a trace moment (TM), where a log–log plot of upscaled fields against resolution λ is taken for each moment q (Eq. 5). The quality of the scaling is given by the estimate r² of the linear regression; the value for q=1.5 is used as a reference. A double trace moment (DTM) is a more robust version of a TM tailored for UM fields, where the moment scaling function K(q,η) of the field ${{\mathit{ϵ}}_{\mathit{\lambda }}}^{\left(\mathit{\eta }\right)}$ (the initial field raised to power η at maximum resolution and re-normalized) is expressed as a function of the multifractal index α (Lavallée et al., 1993).

$$\begin{array}{}\text{(10)}& \langle ({{\mathit{ϵ}}_{\mathit{\lambda }}}^{\left(\mathit{\eta }\right)}{)}^q\rangle \approx {\mathit{\lambda }}^{K(q,\mathit{\eta })}={\mathit{\lambda }}^{{\mathit{\eta }}^{\mathit{\alpha }}K\left(q\right)}\end{array}$$

From the above equation, a value of α can be obtained as the slope of the linear part, where K(q,η) is represented for a given q as a function of η in the log–log plot. Both the TM and DTM techniques give reliable estimates as long as H<0.5 for the studied field.

Since multifractal processes are generated by cascade processes, the average values can become too concentrated over a certain area, leading to spurious estimates of moments above a particular value of q (at q_D, q is above $K\left(q\right)\approx +\mathrm{\infty }$). This effect is called divergence of moments. The convex natures of the functions K(q) and c(γ) are also limited by the sample size of the data or the maximum value of the scale-invariant threshold or singularity (γ_s) and the corresponding moment (q_s). The details of their computation can be found in Schertzer and Lovejoy (1992), Schertzer and Lovejoy (1989), and Lovejoy and Schertzer (2007). For reliable statistical estimates of the moment scaling function and hence the UM parameters, the moment orders used should not exceed q_s (moment order corresponding to the maximum singularity) or q_D (moment order where divergence happens).

An in-depth discussion of the methodological choices we have made, along with an overview of other multifractal formalisms and their strengths and weaknesses, is provided in Appendix A.

3 Turbine power, biases, and associated issues in data analysis

3.1 Turbine power and biases

For the Vestas V-90 instruments, the rated power is 2 MW; this means that the maximum power the turbine can produce is 2000 kW. However, if we calculate the available power as per Eq. (1), there are many instances where it can go beyond the rated value (see Fig. 4c). When analysing the variability of a field using statistical methods, the presence of instrumental limits in the data (here an upper limit) can introduce biases. As briefly mentioned in the Introduction section, an instrumental lower threshold in the data can increase α and decrease C₁ (Jose et al., 2021). In addition to this, there is also bias from the presence of zeroes in the data (Gires et al., 2014) (underestimation of α, deterioration of scaling), which replaced negative values of the turbine power. Figure 4 shows the real and theoretical turbine power state curves along with the bias this poses in statistical analysis. Along with the power produced, the turbine data provide wind velocity at the hub (from a basic sensor installed on the hub), which is used for its internal monitoring. For research purposes, the wind velocity from the 3D anemometer at the mast is more desirable as it offers a more reliable measurement (on almost the same horizontal plane as the turbine hub). Figure 4a shows the empirical state curve of the turbine with this velocity, and Fig. 4b shows the same curve with the velocity from the anemometer. There is considerably more scatter with the latter. It should be stated that the turbines are not in the exact location of the mast (Turbines 8 and 9 are ≈ 3.5 km away), and hence approximation of the wind velocity from the mast (for computing the theoretical power in Eq. 1) comes with some biases.

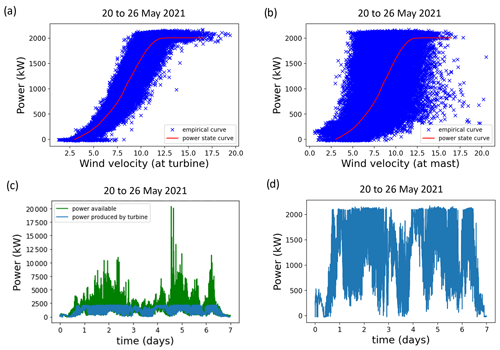
Figure 4 Illustration of the upper threshold (by virtue of a rated power of 2000 kW) in power produced by turbines. (a) Empirical and theoretical power state curve of Turbine 1 with wind velocity from the turbine. (b) Wind velocity from location 1 on the mast. (c) Power produced by the turbine (P_t) and actual wind power available P_a. (d) Effect of the rated power as a threshold of the time series and effect of negative values on P_t for 1-week-long data – 20 to 26 May 2021.

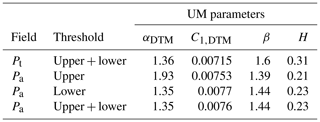
From Fig. 4c and d, it can be clearly seen that the rated power imposes an upper threshold on the turbine power (P_t), while the power available (P_a) is the actual underlying field. For this 1-week-long series of P_t, 21.7 % of the data were at an upper threshold and 2.9 % were either zero or negative (taken as zeroes in the analysis); this percentage was found to change according to the data selected. The effect of these limits on UM analysis is shown in Fig. 5a, where the data in Fig. 4 are treated as an ensemble of 32 min. UM analysis was performed on direct fields as the values of H were within acceptable limits (H<0.3). A unique scaling regime from 15 s to 32 min was considered. The presence of the rated power clips the values of the field and results in a reduced value of α for P_t (Fig. 5a: α=1.36, C₁=0.00715) from that of P_a (Fig. 5b: α=1.93, C₁=0.01753). Imposition of a similar threshold ($P_{\mathrm{a}}<=\mathrm{2000}=\mathrm{2000}$) on P_a was found to artificially reduce the estimates (α from 1.93 to 1.39, C₁ from 0.10753 to 0.0076) in Fig. 5c, bringing them closer to that of biased turbine power, P_t (Fig. 5a). Even closer values of α were obtained when a lower threshold was also imposed (replacing P_a values with zeroes at positions where P_t was negative), giving α a value of 1.35 and C₁ a value of 0.0077 (Fig. 5d). The results are compiled in Table 1. The scaling quality remained similar for all the cases mentioned here, with the r² value (of the TM curve at q=1.5) remaining around 0.99 (second column of Fig. 5).

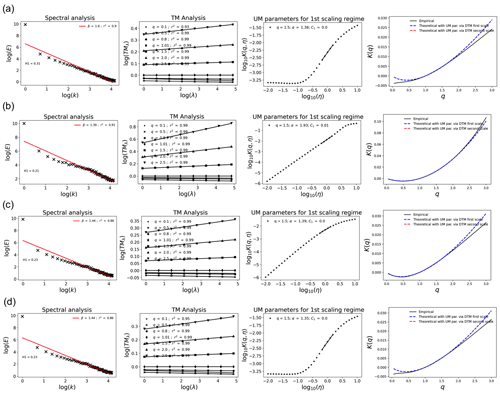
Figure 5 Spectral analysis (Eq. 3), TM analysis (Eq. 5), DTM curve (Eq. 10), and K(q) for (a) power produced by a turbine (P_t) with intrinsic thresholds (upper: due to rated power; lower: due to negative values that are treated as zeroes); (b) power available (P_a), which is the unbiased actual field; (c) P_a, where an upper threshold is imposed at the rated power of the turbine (i.e. all values of P_a above the rated power of the turbine are artificially replaced by 2 MW; values > rated power = rated power); and (d) P_a, where an upper threshold and a lower threshold (values set to zero, where P_t<0) are imposed based on the turbine values. Data used: time series from 20 to 26 May 2021, with the lowest time step of 15 s and a sample size of 32 min.

Table 1 Values of UM parameters for (a) the power produced by the turbines (P_t), which has intrinsic thresholds (21.7 % as the upper threshold and 2.9 % as the lower threshold); (b) the power available (P_a) without any thresholds; (c) P_a with an imposed upper threshold; and (d) P_a with an imposed upper threshold and a lower threshold. The graphs can be seen in Fig. 4.

It should be noted that the effect of a threshold could be different according to the size of the sample and the scaling regimes studied. In the same spirit as σ_e in Jose et al. (2021), the effect of rated power as an upper threshold on P_t is explored here in the theoretical framework of UM. The effect on different scaling regimes as well as the additional complexity from the known effect of zeroes (Gires et al., 2012), though identified here, are not considered to avoid complexity.

3.2 Understanding the effect of upper threshold in the UM framework

Let us take the upper threshold (rated power in this case) at the largest possible scale ratio as

$$\begin{array}{}\text{(11)}& T={\mathrm{\Lambda }}^{{\mathit{\gamma }}_{\mathrm{T}}},\end{array}$$

where γ_T is the singularity corresponding to threshold T and Λ is the maximum resolution (length of the time series). For multifractal fields, the probabilities of exceeding scale-independent thresholds, λ^γ, scale with resolution λ (see Eq. 4). At the upper threshold T, this yields

$$\begin{array}{}\text{(12)}& \text{Pr}({\mathit{ϵ}}_{\mathit{\lambda }}\ge T)\approx {\mathit{\lambda }}^{-c\left({\mathit{\gamma }}_{\mathrm{T}}\right)}.\end{array}$$

If we set the upper threshold, i.e. set all the values of the field greater than T equal to T (represented here by this expression: $\mathit{\{}{\mathit{ϵ}}_{\mathit{\lambda }}\ge T\mathit{\}}=T$), the probability of having values greater than T, Pr(ϵ_λ>T), becomes 0, reducing the above relation into $\text{Pr}({\mathit{ϵ}}_{\mathit{\lambda }}=T)\approx {\mathit{\lambda }}^{-c\left({\mathit{\gamma }}_{\mathrm{T}}\right)}$. This leaves the value of c(γ) equal to +∞ for singularities above γ_T (for γ>γ_T, $c\left(\mathit{\gamma }\right)=+\mathrm{\infty }$). Here, c(γ_T) is the limiting non-zero value above which c(γ) becomes +∞.

This effect of the upper threshold ($c\left(\mathit{\gamma }\right)\to +\mathrm{\infty }$ for γ>γ_T) is similar to the effect of the sampling dimension (D_s) in the UM framework. The maximum observable singularity can be defined by taking the probability at the corresponding threshold as in Eq. (12):

$$\begin{array}{}\text{(13)}& \text{Pr}({\mathit{ϵ}}_{\mathit{\lambda }}\ge {\mathit{\lambda }}^{{\mathit{\gamma }}_S})\approx {\displaystyle \frac{\mathrm{1}}{N_{\mathrm{s}}{\mathit{\lambda }}^D}},\end{array}$$

where N_s is the number of samples and λ^D is the number of values per sample. $N_{\mathrm{s}}={\mathit{\lambda }}^{D_{\mathrm{s}}}$ (D_s being the sampling dimension, which quantifies the number of independent samples with resolution λ; for one sample, D_s=0). Using the notions of D_s and D, with γ corresponding to the sampling resolution, γ_s can be estimated from c(γ_s), $c\left({\mathit{\gamma }}_{\mathrm{s}}\right)=D+D_{\mathrm{s}}$ (Hubert and Carbonnel, 1989; Lovejoy and Schertzer, 2007).

The moment scaling function K(q) and co-dimension function c(γ) were discussed earlier in terms of UM parameters in Eqs. (6) and (7). Both are equivalent functions, and for multifractals they are related by a simple Legendre transform (Parisi and Frisch, 1985; Schertzer and Lovejoy, 1993):

$$\begin{array}{}\text{(14)}& \begin{array}{rl}& K\left(q\right)=\underset{\mathit{\gamma }}{max}[q\mathit{\gamma }-c(\mathit{\gamma }\left)\right],\\ & c\left(\mathit{\gamma }\right)=\underset{q}{max}[q\mathit{\gamma }-K(q\left)\right].\end{array}\end{array}$$

Hence, for every singularity γ, there is a corresponding order of moment q associated with it and vice versa: $q=c^{\prime }\left({\mathit{\gamma }}_q\right)$ and $\mathit{\gamma }=K^{\prime }\left(q_{\mathit{\gamma }}\right)$.

When γ>γ_s, c(γ) = +∞; by Legendre transform K(q) becomes linear from $q>q_{\mathrm{s}}=c^{\prime }\left({\mathit{\gamma }}_{\mathrm{s}}\right)$:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}& {\mathit{\gamma }}_{\mathrm{s}}={\mathit{\alpha }}^{\prime }{C}_{\mathrm{1}}{\left({\displaystyle \frac{D+D_{\mathrm{s}}}{C_{\mathrm{1}}}}\right)}^{\frac{\mathrm{1}}{{\mathit{\alpha }}^{\prime }}}-{\displaystyle \frac{C_{\mathrm{1}}}{\mathit{\alpha }-\mathrm{1}}},\\ & q_{\mathrm{s}}={\left({\displaystyle \frac{D+D_{\mathrm{s}}}{C_{\mathrm{1}}}}\right)}^{\frac{\mathrm{1}}{\mathit{\alpha }}}.\end{array}\end{array}$$

In the case of the sampling dimension, c(γ) varies as follows:

$$\begin{array}{}\text{(16)}& c\left(\mathit{\gamma }\right)=\left\{\begin{array}{lll}+\mathrm{\infty }& \text{for}& \mathit{\gamma }>{\mathit{\gamma }}_s\\ D+D_{\mathrm{s}}& \text{for}& \mathit{\gamma }={\mathit{\gamma }}_s\\ c\left(\mathit{\gamma }\right)& \text{for}& \mathit{\gamma }<{\mathit{\gamma }}_s\end{array}\right\}.\end{array}$$

Similarly, in the presence of the upper threshold here ($\mathit{\{}{\mathit{ϵ}}_{\mathit{\lambda }}\ge T\mathit{\}}=T$), c(γ) reaches +∞ at an earlier limiting value c(γ_T), where γ_T<γ_s (Fig. 6a).

$$\begin{array}{}\text{(17)}& c_{\mathrm{T}}\left(\mathit{\gamma }\right)=\left\{\begin{array}{lll}+\mathrm{\infty }& \text{for}& \mathit{\gamma }>{\mathit{\gamma }}_T\\ c\left({\mathit{\gamma }}_{\mathrm{T}}\right)& \text{for}& \mathit{\gamma }={\mathit{\gamma }}_T\\ c\left(\mathit{\gamma }\right)& \text{for}& \mathit{\gamma }<{\mathit{\gamma }}_T\end{array}\right\}\end{array}$$

Here, γ_T is defined from the threshold as initially stated in Eq. (11), and c_T(γ) is estimated as above. From this, the corresponding limit moment q_T can be obtained as in Eq. (15).

$$\begin{array}{}\text{(18)}& q_{\mathrm{T}}={\left({\displaystyle \frac{c\left({\mathit{\gamma }}_{\mathrm{T}}\right)}{C_{\mathrm{1}}}}\right)}^{\frac{\mathrm{1}}{\mathit{\alpha }}}\end{array}$$

To summarize, in standard data analysis with sampling limitations, c(γ) is bounded by a maximum value c(γ_s), above which it becomes infinite. K(q), which is connected to c(γ) through Legendre transform (Eq. 14), becomes linear beyond this q (q≥q_s) value ($K\left(q\right)=(q-q_{\mathrm{s}}){\mathit{\gamma }}_{\mathrm{s}}+K\left(q_{\mathrm{s}}\right)$). Similarly, in this specific case, when an upper threshold is imposed ($\mathit{\{}{\mathit{ϵ}}_{\mathit{\lambda }}\ge T\mathit{\}}=T$), K(q) becomes linear at an earlier value of q (at q_T<q_s) as defined by γ_T (Fig. 6b).

$$\begin{array}{}\text{(19)}& K_{\mathrm{T}}\left(q\right)=\left\{\begin{array}{lll}{\mathit{\gamma }}_{\mathrm{T}}(q-q_{\mathrm{T}})+K\left(q_{\mathrm{T}}\right)& \text{for}& q>q_{\mathrm{T}}\\ K\left(q_{\mathrm{T}}\right)=q_{\mathrm{T}}{\mathit{\gamma }}_{\mathrm{T}}-c\left({\mathit{\gamma }}_{\mathrm{T}}\right)& \text{for}& q=q_{\mathrm{T}}\\ K\left(q\right)& \text{for}& q<q_{\mathrm{T}}\end{array}\right\}\end{array}$$

Using the DTM technique, for a given q, $K(q,\mathit{\eta })=K\left(q\mathit{\eta }\right)-qK\left(\mathit{\eta }\right)$, which for UM fields is η^αK(q). When no thresholds are applied, K(q,η) varies as

$$\begin{array}{}\text{(20)}& K(q,\mathit{\eta })=\left\{\begin{array}{lll}(q-\mathrm{1})(D+D_{\mathrm{s}})& \text{for}& \mathit{\eta }\ge {\mathit{\eta }}_{+}\left(q\right)\\ {\mathit{\eta }}^{\mathit{\alpha }}K\left(q\right)& \text{for}& \mathit{\eta }<{\mathit{\eta }}_{-}\left(q\right)\end{array}\right\},\end{array}$$

where η₊(q) corresponds to the maximum values of η above which K(q,η) becomes a plateau due to sampling limitations (Eq. 15). To elaborate, K(q,η) consists of two parts K(qη) and K(η), and η₊(q) corresponds to the value of η above which both are linear (which is q_s). The transition to the plateau starts at the lower value η₋(q) (which is $q_{\mathrm{s}}/q$), above which only K(qη) is linear. In the presence of an upper threshold ($\mathit{\{}{\mathit{ϵ}}_{\mathit{\lambda }}\ge T\mathit{\}}=T$), the DTM curve will be (Fig. 6c)

$$\begin{array}{}\text{(21)}& K_{\mathrm{T}}(q,\mathit{\eta })=\left\{\begin{array}{lll}(q-\mathrm{1})c\left({\mathit{\gamma }}_{\mathrm{T}}\right)& \text{for}& \mathit{\eta }\ge {\mathit{\eta }}_{+}\left(q\right)\\ {\mathit{\eta }}^{\mathit{\alpha }}K\left(q\right)& \text{for}& \mathit{\eta }<{\mathit{\eta }}_{-}\left(q\right)\end{array}\right\},\end{array}$$

where η₊(q) = q_T and η₋(q) = $q_{\mathrm{T}}/q$.

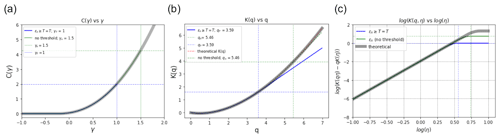
Figure 6 Influence of the threshold on (a) the c(γ)–γ curve, with c(γ) reaching +∞ at γ_T and then γ_s; (b) the DTM curve, with K(q) becoming linear at q_T and then q_s; and (c) the K(q)–q curve, with K(q,η) reaching the upper plateau early. Arbitrary values were used for γ_s and γ_T; UM parameter values of the fields were taken to be α=1.8 and C₁=0.2.

It is important to note here that the value of K(q,η) does not reach the upper plateau abruptly at q_T or q_s. Rather, it flattens gradually, starting from a value of η = $q_{\mathrm{s}}/q$ or $q_{\mathrm{T}}/q$ (as per the value of qη in K(q,η)). The presence of the upper threshold shifts this starting point and decreases the range of possible values for estimation of α (slope of the DTM curve). Hence, the presence of a plateau will result in biased (reduced) estimates.

3.3 Numerical simulations

Underestimation of values of α due to application of the upper threshold was already observed in Fig. 5c using real data. To understand this further, conservative multifractal fields (H=0) were simulated using discrete cascades with values of UM parameters close to those observed for empirical powers (P_t). Discrete cascade simulation here involves division of a parent structure into sub-structures (retaining the value of the parent structure multiplied by a random factor; Chambers et al., 1976), iteratively following a non-infinitesimal scale ratio while maintaining the validity of Eqs. (5) and (6).

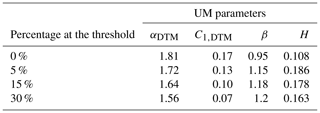
For ease of contrast with the simulations examining lower thresholds in Jose et al. (2021), values of α=1.8 and C₁=0.2 were used. UM analysis was implemented in ensembles (sample size 128 and number of samples 100) by progressively applying the upper threshold till the percentages were observed in P_t (∼ 30 %). K(q) becomes linear at earlier and earlier values of q (after q_T), and an increasing percentage of values at the threshold can be seen in the third column (like in Fig. 6b). The DTM curve in the second column shows that both α and C₁ decrease with progressive application of the thresholds (from 0 % to 30 %: α decreased from 1.8 to 1.56, while C₁ decreased from 0.17 to 0.05).

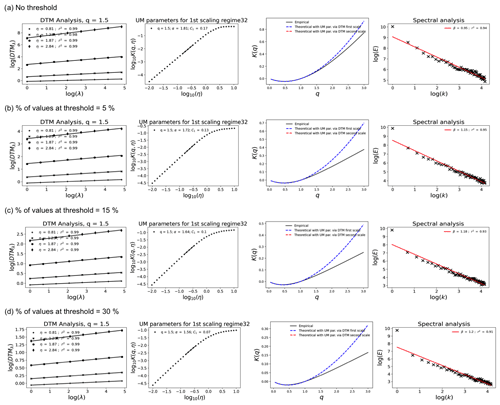
Figure 7 Effect of the upper thresholds illustrated using numerical simulations – discrete cascades of size 128 with 100 samples with α=1.8 and C₁=0.2 as input. The thresholds were applied progressively to the simulated field: (a) no threshold, (b) 5 %, (c) 15 %, and (d) 30 %. A decrease in α and an increase in C₁ with a threshold can be seen from the DTM curves (second column) of panels (a) to (d).

Table 2 Values of the UM parameters for the simulated fields with an artificial imposition of the upper thresholds.

While discussing this bias in the framework before, it was mentioned that the upper threshold was introduced at the maximum resolution (Eq. 11, ${\mathrm{\Lambda }}^{{\mathit{\gamma }}_{\mathrm{T}}}$). Since in practice the lower scales in UM are obtained from averaging the outer scale (at the maximum resolution), the threshold values (and hence γ_T) at each stage do not correspond exactly to the originally defined one. This is the reason for an increased “transition part” (part of the curve from the straight line to the upper plateau) of the DTM curves (second column) in the simulations here (more than that in Fig. 6c). When the estimation of α was forced at η=1 (so that the TM and DTM estimates were the same), the bias in the values of α increased as the slope estimation moved to the transition part. For example, the already biased value of α at the 30 % threshold, 1.58 (slope at log η between −0.1 and −0.5), was further reduced to 0.95 (slope around log η=0). In this estimation, C₁ moreover remained similar to previous estimates at all the thresholds.

It is interesting to note that the trend here (only for α) is not exactly the opposite of what was observed during numerical simulations with lower thresholds in the section (Jose et al., 2021). While the imposition of a lower threshold increased α and decreased C₁, the upper threshold here reduces both UM parameters. In the specific case of turbine power, P_t (Fig. 5a) has a combination of the upper threshold from the rated power and the lower threshold (zeroes) from a negative power (the latter is not considered here). This, in practice, further reduces the range of available η for estimation of α by imposing a lower plateau as well (see Fig. 5, third column). Also, the effect of this bias could be different when fluctuations of the fields are selected to retrieve conservative fields since the simulations were performed directly on conservative multifractal fields here. Since two consecutive power values can be the same, thanks to the rated power, taking fluctuations will yield zeroes in the field and add to the zero bias. The effect of both biases could be different when the aggregate power of the wind farm is considered as well: this is not explored here either.

3.4 Data analysis reducing the biases

So far, the effect of thresholds in UM analysis has been illustrated in the framework of UM. To get a better idea of their effect on scaling, UM analysis was performed of a longer series of powers. For this, a 3-month-long continuous series was taken (from 1 January to 1 April 2021) and UM analysis was performed on P_a and P_t as ensembles of sample size 128 (32 min). Figure 8a and b show the curves for P_a (α: 1.93; C₁: 0.01) and P_t (α: 1.11; C₁: 0.0042) respectively. Considering P_a to be the underlying field, the effects of the thresholds (upper and due to zeroes) in P_t can be seen in the DTM curve (Fig. 8b, second row). The lower plateau corresponds to the presence of a negative power in the data (which was replaced by zeroes), and the low value of α is due to η being in the transition range (as already seen in Fig. 6c). Figure 8c and d show the UM analysis for the same data but remove the columns with thresholds. In the P_t ensemble data, the columns with thresholds, zeroes, and repetition of data were removed by using a limit of 0.01 %. For example, columns with more than 0.01 % of their values ≥1600 were removed to be on the safe side when analysing data without the influence of a threshold. For a more accurate comparison, the same columns were removed from P_a as well; the results are shown in Fig. 8c (α: 1.76; C₁: 0.0095) and Fig. 8d. It can be seen that the lower plateau disappeared for P_t and that the values of the UM parameters (α: 1.5749 from 1.11; C₁: 0.00554 from 0.0042) improved; this also increased the value of β (1.8 from 1.6) and consequently that of H (0.41 from 0.3). It should be noted that the values of the UM parameters get closer to those of P_a but are not the exact values. This suggests that there are slight differences in the properties of both fields, even though they appear comparable when biases are removed.

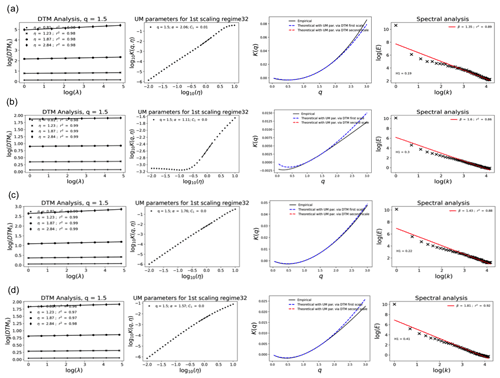
Figure 8 UM analysis of data from 1 January to 1 April 2021 as ensembles of sample size 128 (32 min): (a) P_a (as the data are), (b) P_t (as the data are), (c) P_a (columns with the threshold removed on the basis of the P_t data below), and (d) P_t with the columns of the upper threshold and zero data removed.

4 Conclusion

Wind turbines are designed to work at a rated power for optimal production of power as well as their safe functioning. This inadvertently creates an upper threshold in the output data of power production, and such an effect induces biases in statistical analysis, especially when the small-scale non-linear variability and intermittency are to be studied. The backdrop of this study followed the campaign in Gires et al. (2022), where the main objectives were to analyse the turbine power P_t as a temporal field and to gain insights into its correlation with rainfall, which is poorly understood, and also with other meteorological fields, across scales using the data averaged to these reliable frequencies. However, direct analysis of empirical turbine power (using the framework of UM) was found to be difficult since the output from wind turbines is limited by a maximum or rated power. In time series analysis this acts as an upper threshold, resulting in reduced estimates of UM parameters compared to those of theoretically available wind power (P_a) for extraction. The reason for this decrease was identified in the framework of UM and is illustrated using theoretical formulations. The same has been confirmed through simulations of conservative multifractal fields as well. Basically, the presence of an upper threshold introduces an upper plateau into the DTM curve, which is similar to the one due to the sampling dimension, but it begins at a lower value of η. This reduces the range of available η values for estimation of the slope and hence results in a biased value of α (reduced α and C₁). Also, when it comes to the empirical power produced by the turbines, the biases are two-fold since a lower threshold (albeit to a much lesser extent) is involved, because the turbine does not necessarily always produce power and has moments that involve only operational consumption (leaving power production values negative). Since UM in their usual forms are not designed to handle negative values, based on how these values are managed (taken to be zero here), the values of α will be biased further due to the effect of a lower threshold.

Though these biases have been identified, as of now, no solutions are available to account for them, and more methodological developments are required for this solution. The same is required to understand the combined effect of both biases. It is also worth mentioning that such an upper threshold is very likely to affect other statistical analyses relying on scale invariance as well. However, this is beyond the scope of the current paper and would require separate investigations. Due to the presence of the above-mentioned biases in P_t, the actual wind power available at the turbine hub for extraction ($P_{\mathrm{a}}=f(v,\mathit{\rho })$; Eq. 1) was used as a proxy to understand the small-scale variability in the follow-up UM analysis. Since the presence of thresholds in the data – imposed by limitations of operations as well as measurement – exists in many geophysical situations, understanding them is important for retrieving the actual characteristic parameters and modelling them. In the case explored here, since the characterization of power production already suffers from various influences that are poorly understood and accounted for, understanding the biases in the data treatment will help avoid more uncertainties.

Appendix A: Diversity of multifractal formalisms and theoretical choices

In response to questions from referees and therefore potential questions from readers, we felt it necessary to discuss in greater depth the methodological choices we have made. The purpose of this Appendix is therefore to provide, in a fairly autonomous way to ease reading, a better overview of the formalisms, highlighting their strengths and weaknesses, their common features, and their diversity. This Appendix is also valid for Part 2 of this publication.

A1 Deterministic and stochastic multifractals as well as dimension and co-dimension formalisms

In this paper and its companion paper (Jose et al., 2024), we use a stochastic multifractal framework (Schertzer and Lovejoy, 1984, 1983, 1989, 1992), for the fundamental reason that it is much more general than a deterministic multifractal framework (Parisi and Frisch, 1985; Halsey et al., 1986). This large difference is fundamentally due to the number of samples required to get reliable information. While a unique sample is sufficient for a purely deterministic process, the determination of extremes of a stochastic process may require a very large number of samples. This difference is also illustrated by the fact that a stochastic event has a finite occurrence frequency, while it may occur on an infinite number of samples. This results from the fact that a probability frequency can be understood as the (finite) limit of the ratio of two diverging numerations: “favourable cases” and “all cases”. If both numerations scale with a dimension exponent, then the frequency scales with the difference of these dimensions, which is usually called co-dimension. This can be written as follows for a process ε_λ at resolution $\mathit{\lambda }=L/\mathrm{\ell }$ (outer scale L, observation scale ℓ) when assessing its probability of diverging more quickly than λ^γ, i.e. with a singularity γ:

$$\begin{array}{}\text{(A1)}& \begin{array}{rl}\text{Pr}({\mathit{\epsilon }}_{\mathit{\lambda }}\ge {\mathit{\lambda }}^{\mathit{\gamma }})& \approx {\displaystyle \frac{N_{\mathit{\lambda }}({\mathit{\epsilon }}_{\mathit{\lambda }}\ge {\mathit{\lambda }}^{\mathit{\gamma }})}{N_{\mathit{\lambda }}}}\approx {\displaystyle \frac{{\mathit{\lambda }}^{D\left(\mathit{\gamma }\right)}}{{\mathit{\lambda }}^D}}={\mathit{\lambda }}^{D\left(\mathit{\gamma }\right)-D}\\ & ={\mathit{\lambda }}^{-c\left(\mathit{\gamma }\right)},\end{array}\end{array}$$

where the co-dimension c(γ) and the dimension D(γ) satisfy

$$\begin{array}{}\text{(A2)}& D=c\left(\mathit{\gamma }\right)+D\left(\mathit{\gamma }\right),\end{array}$$

where D is the embedding dimension of the process and thus generalizes the definition of the co-dimension C(A) of a D(A)-dimensional sub-space A in a D-dimensional vector space:

$$\begin{array}{}\text{(A3)}& D=D\left(A\right)+C\left(A\right).\end{array}$$

Equation (A1) provides the first insight into the fundamental fact that scaling exponents of probabilities are co-dimensions, while those of numerations are dimensions.

It seems paradoxical that the dimension or deterministic multifractal formalism was introduced to explain the observed non-linearity of statistical scaling exponents, specifically that of the velocity structure functions (Anselmet et al., 1984), which are the statistical moments of the velocity increments. This was done with the help of strong assumptions: the singularities of the velocity increments, defined as local Holder exponents, were assumed to be geometrically and rather deterministically distributed over embedded fractals. In many respects, the f(α) formalism (Halsey et al., 1986), which deals with multifractal strange attractors, further emphasized this implicit non-random and geometric framework. A dimension formalism such as the f(α) formalism is formally related to the co-dimensions (γ,c(γ)) according to

$$\begin{array}{}\text{(A4)}& {\mathit{\alpha }}_{\mathrm{D}}=D-\mathit{\gamma };f_{\mathrm{D}}\left({\mathit{\alpha }}_{\mathrm{D}}\right)=D-c\left(\mathit{\gamma }\right).\end{array}$$

The sub-index D is introduced to α and f for two reasons:

• Both α and f depend on the embedding dimension D, e.g. by taking cuts of dimensions smaller than D, while (γ,c(γ)) do not depend on it.

• Another “historical” α has a quite different meaning, as briefly mentioned below.

The same dependence on D occurs for the scaling exponent τ(q) of the partition function (Hentschel and Procaccia, 1983; Jiang et al., 2019), which is strongly related to that of the statistical moment scaling exponent K(q),

$$\begin{array}{}\text{(A5)}& <{\mathit{\epsilon }}_{\mathit{\lambda }}>\approx {\mathit{\lambda }}^{K\left(q\right)},\end{array}$$

as follows:

$$\begin{array}{}\text{(A6)}& {\mathit{\tau }}_{\mathrm{D}}\left(q\right)=(q-\mathrm{1})D-K\left(q\right).\end{array}$$

A2 Partial equivalence between dimension and co-dimension formalisms

In fact, we implicitly used the partial equivalence between both formalisms for the introduction of the co-dimension (Eq. A1). Before insisting on its partiality, let us stress that it is merely defined by Eq. (A4), a very broad but rather straightforward generalization of Eq. (A3). Equation (A4) thus defines the framework transformation of going from one formalism to another.

Unfortunately, this equivalence is only partial because the dimension framework is much more limited than the co-dimension one. A major difference is that the numeration dimension D(γ) is bounded below and above ($\mathrm{0}\le D\left(\mathit{\gamma }\right)\le D$), while the co-dimension c(γ)) being statistically defined as the opposite of the scaling exponent of the probability exponent generally has no upper bound (0≤c(γ). For instance, c(γ))=∞ merely corresponds to a singularity γ that almost never happens, including at a finite resolution. According to Eq. (A4), c(γ)>D would correspond to a negative dimension D(γ).

A3 Universality and stochasticity

One important feature of the stochastic framework is that it provides universal behaviour, i.e. processes that are attractive, stable, and determined by only a limited number of parameters. We briefly recall that this is the case for the UM (Schertzer and Lovejoy, 1987, 1997) that satisfy a broad generalization of the central limit theorem: their generators are attractive and stable through re-normalized summations. We recall that their statistics are defined by the three parameters which follow and which are physically meaningful:

• For the scaling exponent H¹ of the mean field, when H=0, the mean field is strictly scale-invariant and the field is said to be conservative. H≠0 often results from a fractional integration of this order of a conservative field.

• The co-dimension C₁≥0 of the mean field measures the mean intermittency, i.e. how the mean fluctuations are increasingly concentrated scale by scale. When C₁=0, there is no intermittency and the field is statistically homogeneous.

• The multifractal index $\mathrm{0}\le \mathit{\alpha }\le \mathrm{2}$ measures the variability of the intermittency when departing from the mean field. When α=0, the field is uni-fractal or mono-fractal: α=2 corresponds to a maximal intermittency and to the so-called log-normal model. α is also the Levy stability index (Lévy, 1937) of the cascade generator.

The corresponding UM scaling moment function is therefore

$$\begin{array}{}\text{(A7)}& K\left(q\right)=-qH+K_{\mathrm{c}}\left(q\right);K_{\mathrm{c}}\left(q\right)=C_{\mathrm{1}}{\displaystyle \frac{q^{\mathit{\alpha }}-q}{\mathit{\alpha }-\mathrm{1}}},\end{array}$$

where K_c(q) denotes the scaling moment function of a conservative UM field. We believe that the case studies of the textual body confirm that Eq. (A7) allows a much richer data analysis than the frequently used deterministic indicators, such as $\mathrm{\Delta }{\mathit{\alpha }}_{\mathrm{D}}={\mathit{\alpha }}_{\mathrm{D},\max }-{\mathit{\alpha }}_{\mathrm{D},\min }$.

A4 Hurst exponent and its multifractal generalizations

Scaling time series analysis has been strongly focused on the estimation of the historical Hurst exponent H (Hurst, 1951), in particular with respect to its critical value H=0.5 that is supposed to discriminate long-range dependency and persistence ($H>\mathrm{1}/\mathrm{2}$) from short-range dependency and anti-persistence ($H<\mathrm{1}/\mathrm{2})$. The multifractal ideology has ruined the dogma of its uniqueness and justified divergent estimates where not accidental, but it did result from a given physics, i.e. that of intermittency. Among the many ways of defining a generalized Hurst exponent (GHE, Gómez-Águila and Sánchez-Granero, 2021), it is straightforward to consider the scaling exponent H(q) of the qth root of the (absolute) qth-order statistical moment of the field ²:

$$\begin{array}{}\text{(A8)}& H\left(q\right)=-K\left(q\right)/q.\end{array}$$

This definition is very generic and is an effective measure of the evolution of the qth-order statistical moment, if any, with respect to its order q. In particular, the uniqueness of H (H(q)≡H) is recovered for fractional integrations of homogeneous processes. By contrast, fractional integrations of multifractal processes yield a non-constant part, e.g. for a fractional integration of a conservative field with the scaling moment function K_c(q):

$$\begin{array}{}\text{(A9)}& H\left(q\right)=H-K_{\mathrm{c}}\left(q\right)/q.\end{array}$$

In the generic case of universal multifractals, K_c(q) only depends on the universal parameters C₁ and α (Eq. A7). Because H(2) is often considered the historical Hurst exponent (Kantelhardt, 2002), it is only equal to H for homogeneous processes according to Eq. (A9).

The main drawback of the generalized Hurst exponent H(q) is that it gives access to the statistics of the cascade generator less directly than with the scaling moment function K(q). This may explain why many GHE studies have limited outputs due to a lack of theoretical guidance, e.g. by only providing raw statistics of H(q) such as its minimum and maximum over a given range of q.

A5 Detrending frameworks

Multi-fractal detrended fluctuation analysis (MFDFA; Kantelhardt, 2002) is a popular scaling analysis technique that explicitly uses the concept of the generalized Hurst exponent. However, this is not done directly on the field of interest but rather on the standard deviations of the residues of polynomial regressions on the running sum of the fluctuations of the original time series. It thus corresponds to a multifractal extension of the (fractal) DFA; Peng et al., 1994), as generally presented.

Let us provide some details about this. Let Y(i) be the cumulative fluctuation of the original time series x(k) of the mean value $<x>$:

$$\begin{array}{}\text{(A10)}& Y\left(i\right)=\sum _{k=\mathrm{1}}^i\left[x\right(k)-<x>].\end{array}$$

The series is split into N_s non-overlapping sub-series of finite size s, and a detrending polynomial y_ν(i) with constant order m is fitted into each sub-series by least squares. This yields the following root mean square variation over the ν^th sub-series:

$$\begin{array}{}\text{(A11)}& F(\mathit{\nu },s)={\left[{\displaystyle \frac{\mathrm{1}}{s}}\sum _{i=\mathrm{1}}^s\mathit{\left\{}Y\right[(\mathit{\nu }-\mathrm{1})s+i]-y_{\mathit{\nu }}(i){\mathit{\}}}^{\mathrm{2}}\right]}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

Averaging over the N_s sub-series of size s yields the total variation for the DFA analysis:

$$\begin{array}{}\text{(A12)}& F\left(s\right)={\left[{\displaystyle \frac{\mathrm{1}}{N_{\mathrm{s}}}}\sum _{\mathit{\nu }=\mathrm{1}}^{N_{\mathrm{s}}}{F}^{\mathrm{2}}(\mathit{\nu },s)\right]}^{\mathrm{1}/\mathrm{2}}\end{array}$$

The generalization to MFDFA is straightforwardly obtained by introducing the statistical order q instead of 2:

$$\begin{array}{}\text{(A13)}& F_q\left(s\right)={\left[{\displaystyle \frac{\mathrm{1}}{N_{\mathrm{s}}}}\sum _{n=\mathrm{1}}^{N_{\mathrm{s}}}\left[F^{\mathrm{2}}\right(\mathit{\nu },s){]}^{q/\mathrm{2}}\right]}^{\mathrm{1}/q}.\end{array}$$

The estimate of H(q) is obtained using the logarithmic slope of F_q(s):

$$\begin{array}{}\text{(A14)}& F_q\left(s\right)\approx s^{H\left(q\right)}\iff H\left(q\right)\approx {\displaystyle \frac{\ln F_q\left(s\right)}{\ln s}}.\end{array}$$

It is similar but not identical to the scaling of the trace moment of the original field.

A6 Deferring to future work

A priori, H(q) is not unique, since it may depend like F_q(s) on the order m of the detrending polynomials y_ν(i), and there is no obvious theoretical guidance on how to choose this order. In addition, the cumulative fluctuation obviously increases the order of integration H by a unit (Eq. A10). Conversely, the obtained estimates (Eq. A14) must be reduced by the same amount to indirectly estimate H(q) for the original series. The most serious theoretical drawback is the linear decomposition into local polynomial trends and stochastic fluctuations. Moreover, as the former is maximized by least squares, the importance of the fluctuations is minimized even though they are initially at the centre of the analysis. Because of these many issues, we defer the MFDA and variants of our data to future work.